為何昨天的 F 是多元二次多項式？

保持昨日所使用的參數：q = 2, n = 5
雙極構造法中「很好算反函數的」F 長這樣：

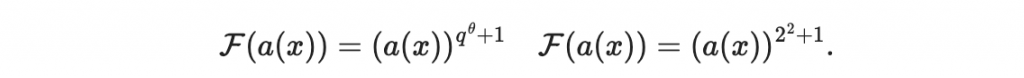
取次方的運算是在以下的多項式環：

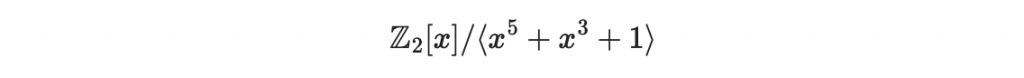
因此，F 是一個輸入多項式，輸出多項式的函數，並且，這些多項式都是小於 5 次。

同時注意到因為係數是 Z_2 裡的數字，這裡面的數字只有 0 與 1 ，並且 1 + 1 = 2 mod 2 = 0 。

在這裡，取平方就是線性映射

首先我們令

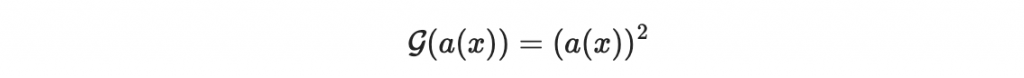
若我們用向量表示法

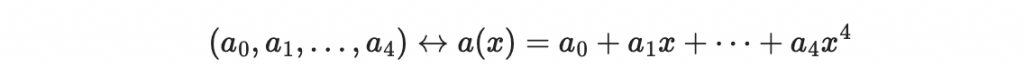
則 G 是一個五維向量空間到五維向量空間的線性映射。

原因是

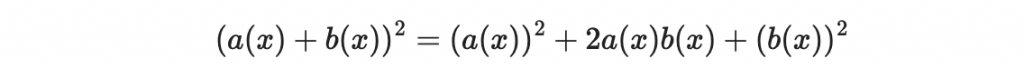
但是因為這些多項式活在一個 1 + 1 = 2 = 0 的世界，所以

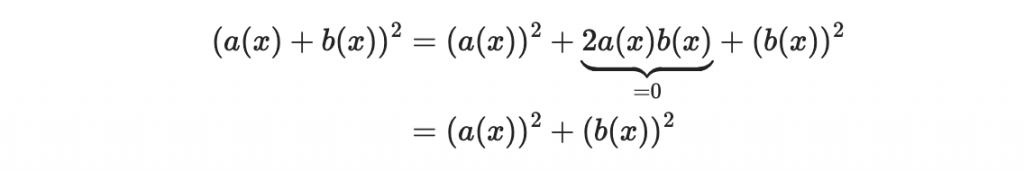
因此我們有

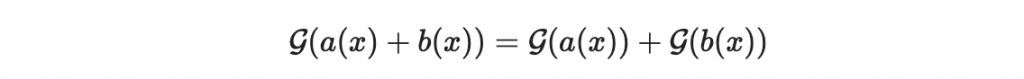
另外，假設 c 是一個在 Z_2 的係數，那

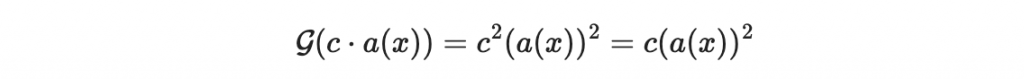
因為如果 c = 0 那 c^2 = 0 = c，如果 c = 1 那 c^2 = 1 = c ，c^2 永遠等於 c。

結論：

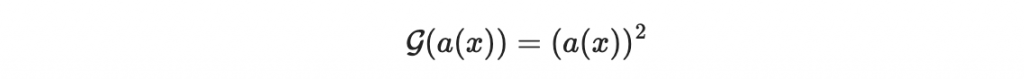
的向量表示法，為一個五維空間到五維空間的線性映射。

在這裡，取很多次平方也是線性映射

現在開始看

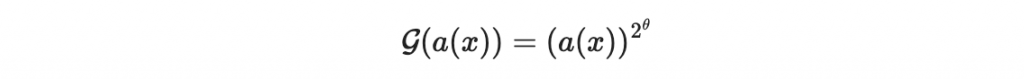
若我們用向量表示法，則 G 是一個五維向量空間到五維向量空間的線性映射。

原因是 a(x) 平方後變成

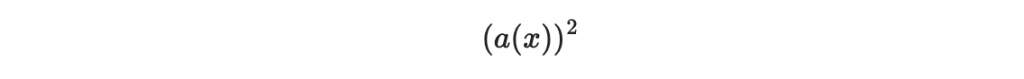
再平方後變成

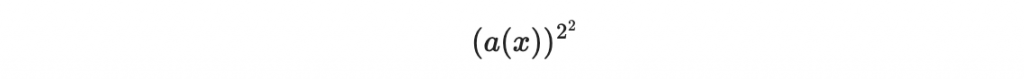
以此類推，原本的 a(x) 經過 theta 次平方後，就可以得到

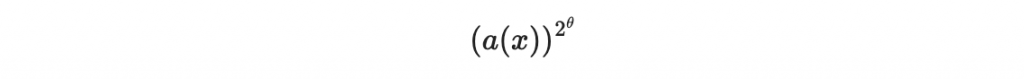
因此，

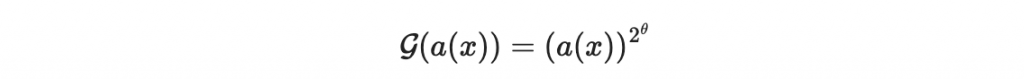
是由 theta 次的平方組合而成。

藉由我們剛剛的結論「平方是線性映射」，我們知道 G 函數是由一連串的線性映射組合而成。

線性映射與線性映射的組合都還是線性映射，因此 G 是一個線性映射。

結論：

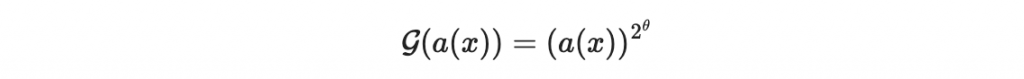
的向量表示法，為一個五維空間到五維空間的線性映射。

回到 F 函數

好，我們回到

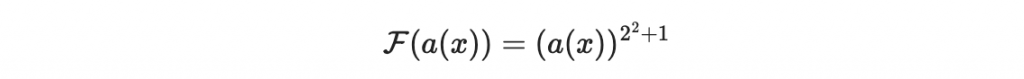
分解 F 函數得到

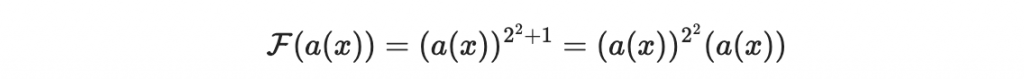
因為取數次的平方都是線性映射，所以上面分解的其中一個成分

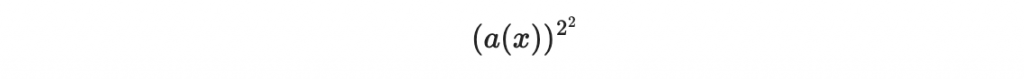
是從 a(x) 做線性映射得來。也因此他的係數應該是如下形式

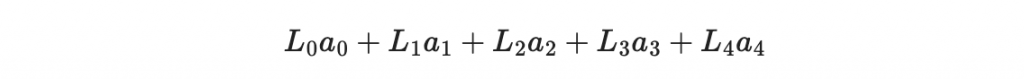
也就是一開始 a(x) = (a0, a1, a2, a3, a4) 的線性組合。

好！因為是關心

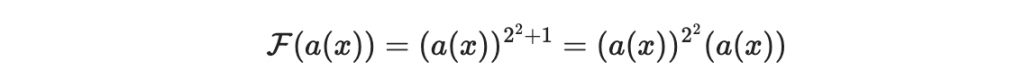
的向量表示法，所以我們來研究他的係數。

首先

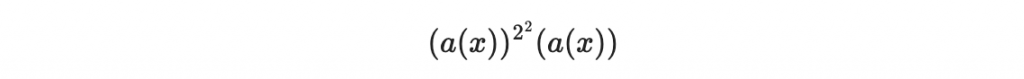
在還沒做模化約（對 x^5+x^3+1 做模除）以前，他的係數應該是一些前者(a(x))^(2^2)的係數乘上後者 a(x) 的係數的和。

所以就是一些

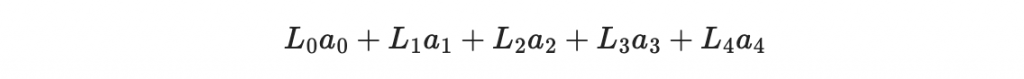
乘上某個 a_i 的和。在這之中，就會產生二次項 a_i * a_j 了。

接著進行麼化約時，超過五次的係數會被加到前面去，在這之中沒有乘法的作用，所以最終的結果

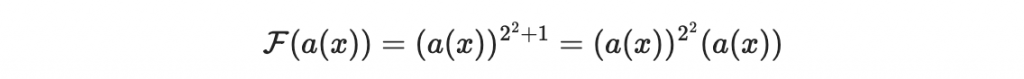
其係數都是由 a_i 等最高二次的項來組成。也因此這個函數的向量表示法可以寫成本來的向量

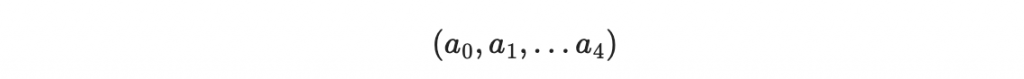
的二次多元多項式系統。

淺談隱藏域方程系統（Hidden Field Equation）

從上面得討論可以得知，

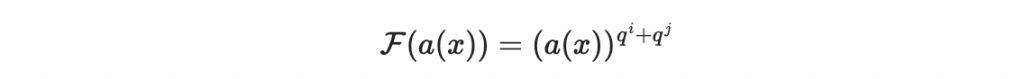
也是一個多元二次多項式系統。原因是因為可以做以下分解

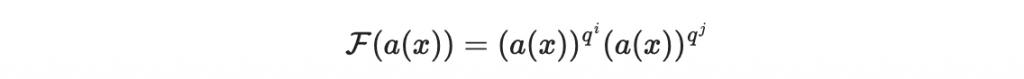
然後

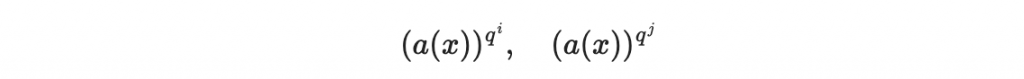
在向量表示法下都是線性映射。

我們於是可以構造

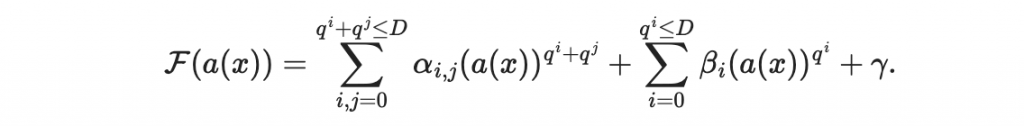
而他也是一個多元二次多項式系統。

很可惜他的反函數並不像 MI 系統那樣簡潔。在解碼時的計算是使用 Berlekamp 演算法來解方程：

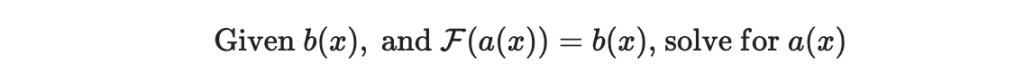
於是就可以使用雙極構造法來做成密碼系統。

Takeaway

• 為何 MI 系統裡面的 F 是多元二次多項式系統？
• 為何 HFE 系統裡面的 F 是多元二次多項式系統？

ref
DING, Jintai; GOWER, Jason E.; SCHMIDT, Dieter S. Multivariate public key cryptosystems. Springer Science & Business Media, 2006.