我們在 Day11 討論了 MI 協議。但是我們在當時所定義的公鑰是以下程式碼：

def Public_key(x):
    x = T(x)
    x = Central_Map_poly(x)
    x = S(x)
    return x

那這不就代表說，當我們公佈公鑰時，其中的私鑰 T, F, S 都必須一起發出去？

另外，在 Day12 討論了 MI 裡面的 F 是多元二次，所以 P(x) = S(F(T(x))) 是一個多元二次多項式系統。今天我們就使用程式來計算這個公鑰 P(x) 於是我們可以把它安全的發出去。

多元二次多項式的矩陣表示法

首先根據 Day12 的內容，我們知道公鑰 P 可以寫成：

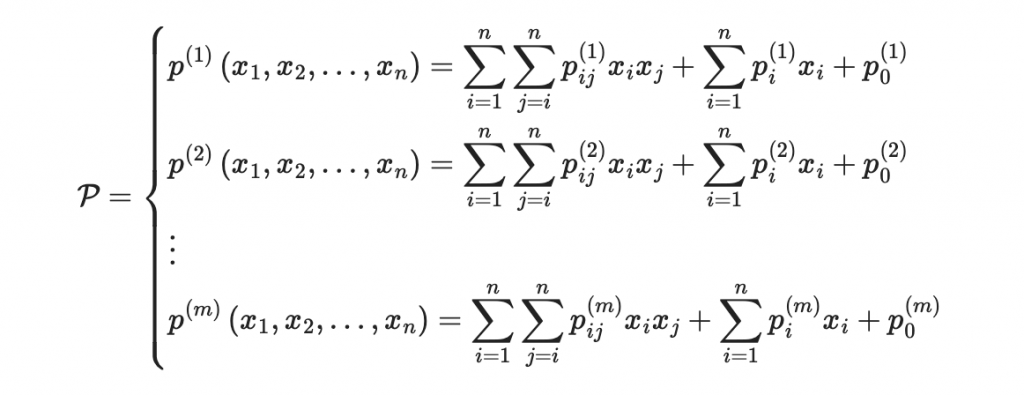
其中係數都是固定的。
如果想要安全地把私鑰送出去，那我們就得乖乖的把上面這些係數通通算出來，然後發送這些係數出去。
為了讓程式好寫，我們在這裡使用矩陣表示法：

首先先看其中第 k 個多元二次多項式：

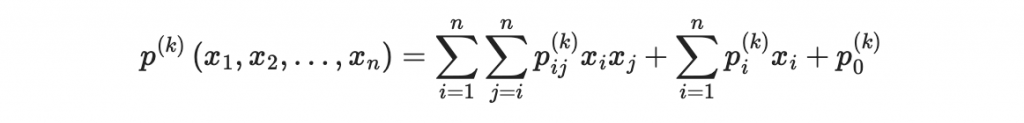
如果把 x 寫成行向量

則有

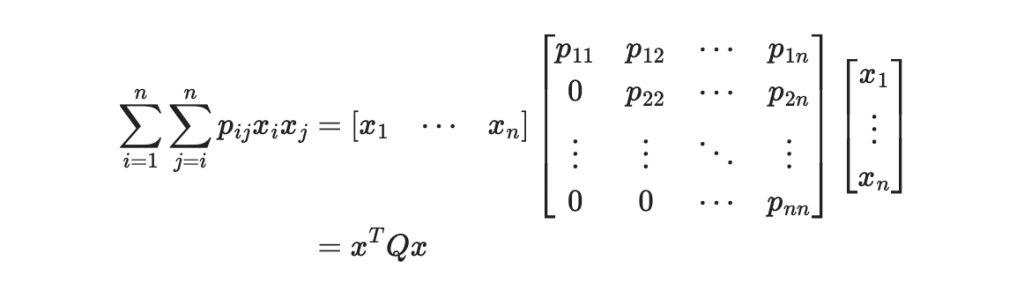
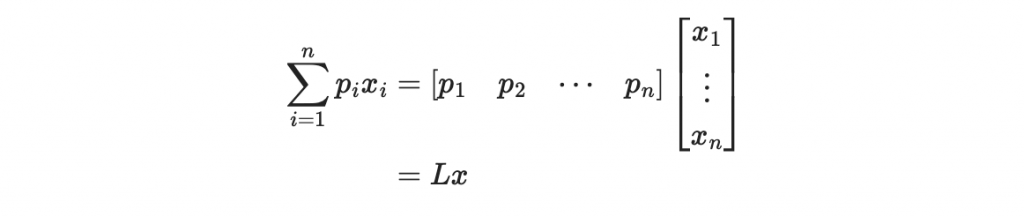
於是我們可以寫出

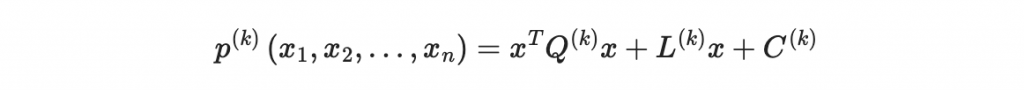
其中

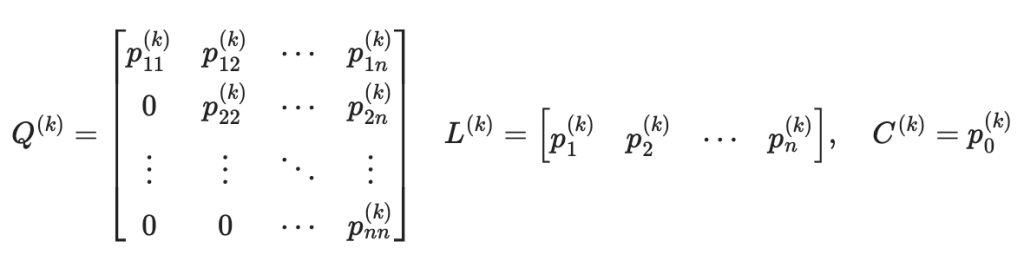
結論：
我們要計算出每個矩陣 Q, L, 以及常數項 C ，然後就可以當作公鑰發出去。

MI 系統裡的特殊觀察

因為我們在 MI 系統內要設定 q = 2，也就是係數是 Z_2 裡面的元素，因此

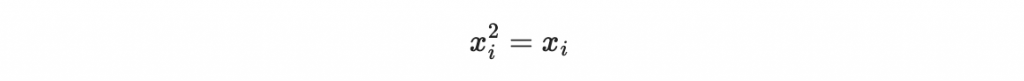
所以所有的線性項都可以當作二次項

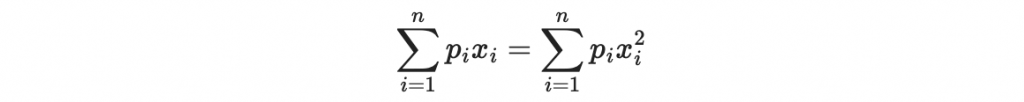
也因此，對 MI 系統來說，我們可以把 p^{(k)} 寫成

計算 MI 系統的公鑰係數

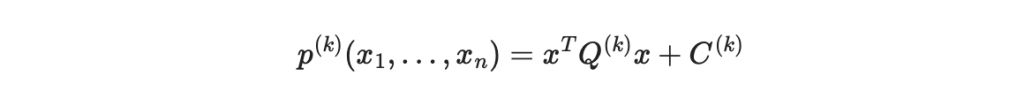
接下來，我們使用 SageMath 來實作這個矩陣表示法，並計算公鑰。

準備工作（再做一次 MI ）

首先，讓我們定義參數和隨機仿射映射

q = 2
n = 5 # degree of g(x)

R = quotient(ZZ, q*ZZ)
R_poly = PolynomialRing(R, 'x')

g = x^5 + x^3 + 1
R_poly_quotient = quotient(R_poly, g)

theta = 2
h = (xgcd((q^n)-1, (q^theta)+1))[2]
h = h + (q^n-1)

# 生成隨機仿射映射
def RandomAffineMapGenerator(n, R):
    while True:
        A = random_matrix(R, n, n)
        if A.is_invertible():
            break
    b = random_vector(R, n)

    def AffineMap(v):
        v = vector(v)
        v = A * v + b
        return v.list()

    def InverseMap(v):
        v = vector(v)
        v = A.inverse() * (v - b)
        return v.list()

    return AffineMap, InverseMap, A, b

S, S_inv, A_S, b_S = RandomAffineMapGenerator(n, R)
T, T_inv, A_T, b_T = RandomAffineMapGenerator(n, R)

def Central_Map_poly(X):
    X = R_poly_quotient(X)
    return (X^(q^theta + 1)).list()

def Central_Map_poly_inv(X):
    X = R_poly_quotient(X)
    return (X^h).list()

def Public_key(x):
    x = T(x)
    x = Central_Map_poly(x)
    x = S(x)
    return x

開始計算係數

我們先把每個 p^{(k)} 的常數項給算出來，並記錄在 C 這個 list 裡面

zero_vector = [0] * n
C = Public_key(zero_vector)

另外定義一個扣掉常數項之後的公鑰映射

def Homogeneous_Public_key(x):
    x = Public_key(x)
    for i in range(n):
        x[i] = x[i] - C[i]
    return x

定義這個之後我們就有

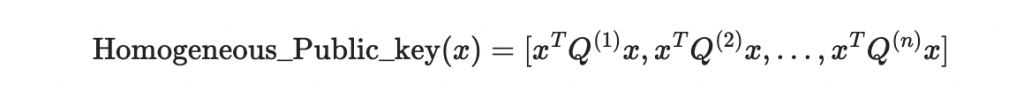
也就是

於是就可以很方便計算 Q^{(k)}.

我們在程式碼裡面使用 Q 來儲存所有的 Q^{(k)}：

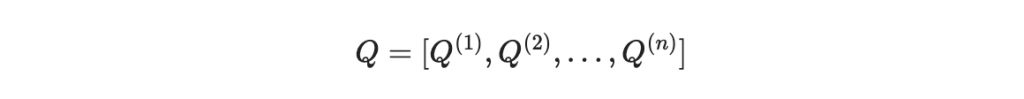
# 先初始化為零，把形狀做好
Q = [[[0 for _ in range(n)] for _ in range(n)] for _ in range(n)]

先計算對角線項：

原理是因為如果 e_i = (0,...,1,...0) （只有在第 i 的位置是 1 其他都是零）那

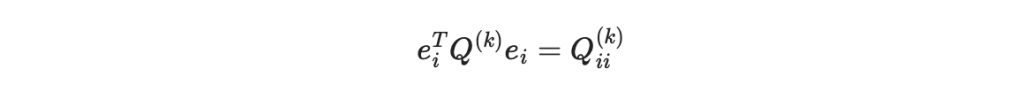
# 計算對角線項
for i in range(n):
    for k in range(n):
        e_i = [0 for _ in range(n)]
        e_i[i] = 1
        Q[k][i][i] = Homogeneous_Public_key(e_i)[k]

接著計算非對角線項：

原理是因為如果 e_ij = (0,...,1,...,1,...0) （只有在第 i, j 的位置是 1 其他都是零）則

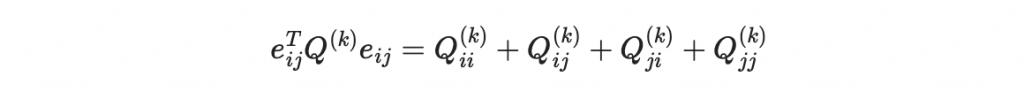
但因為我們所設定的 Q 是上三角矩陣，所以 Q_ji = 0
因此我們知道

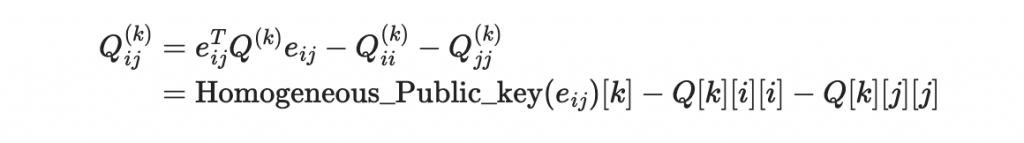
# 計算非對角線項
for k in range(n):
    for i in range(n):
        for j in range(i+1,n):
            e_ij = [0 for _ in range(n)]
            e_ij[i] = 1
            e_ij[j] = 1

            Q[k][i][j] = Homogeneous_Public_key(e_ij)[k] - (Q[k][i][i]) - Q[k][j][j]

好！幾乎完成了！現在已經可以把 Q = [Q^{(1)}, ..., Q^{(n)}] 以及常數項 C 釋出。

驗證正確性

為了驗證正確性，我們進行以下的驗證。

首先把 Q 裡面的每個矩陣 Q^{(k)} 都轉化為 SageMath 裡面的矩陣類別，後面的乘法就可以寫得很簡單：

for k in range(n):
    Q[k] = matrix(Q[k])

於是可以做出以下根據矩陣 Q^{(k)} 以及常數項 C 所做的公鑰：

def Publishable_Public_Key(x):
    x = (Matrix([[x[i]] for i in range(n)]))
    result = []
    
    
    for k in range(n):
        result.append(x.T * Q[k] * x + C[k])


    result = [result[i][0][0] for i in range(n)]

並進行驗證

for _ in range(100):
    x = [R(randint(0,1)) for i in range(5)]
    result = Public_key(x)
    result2 = Publishable_Public_Key(x)
    if not (result == result2):
        print("WRONG Public Key")
        break

# outputs:

如果全對的話就不會有 Outputs 啦！