好！我們來到 MI 系統的最後一篇了！我個人很喜歡 MI 系統，因為他淺顯易懂而且構造簡單演算法也不複雜，但也因為它內部的數學結構太簡單，所以我們今天可以介紹一個「線性化攻擊」。

方法論

數學部分

（如果你對數學不感興趣，可以直接滑到結論與攻擊的部分）
回顧多項式與向量的對應關係

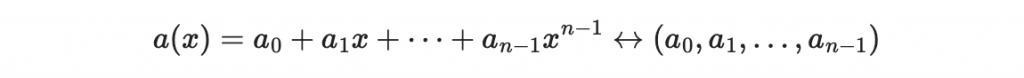
我們使用以下的符號

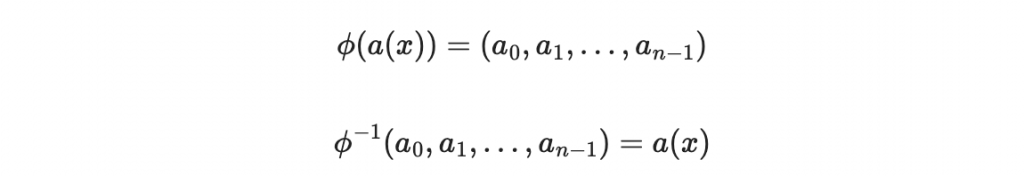
這個 phi 函數，在數學上叫做「同構」（isomorphism）

考慮一個明文：

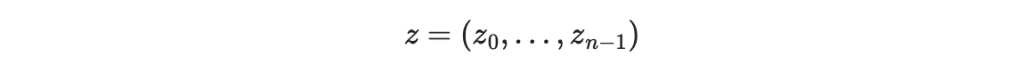
加密過後變成

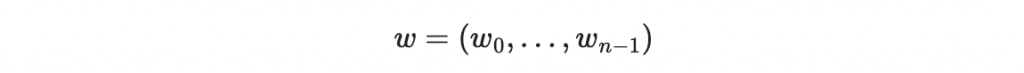
那我們說 z / w 是一個「明文/密文對」（plaintext/ciphertext pair）
注意到我們作為一個攻擊者，因為公鑰 P(x) = S(F(T(x))) 是公開的，所以我們可以創造很多個明文/密文對。（你也可以藉此進行暴力破解法）

現在假設私鑰是 S, F, T ，其中 S 與 T 是可逆仿射變換、F 是中間映射：

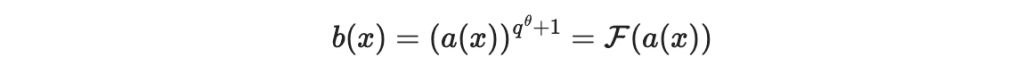
現在，兩邊同取 q^theta - 1 次方

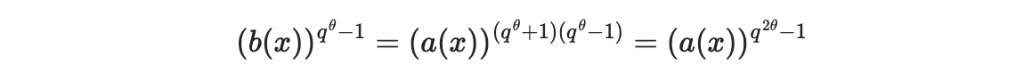
然後左右同乘 a(x)b(x)

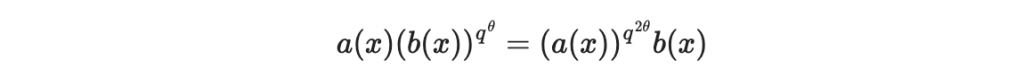
並定義 R 函數：

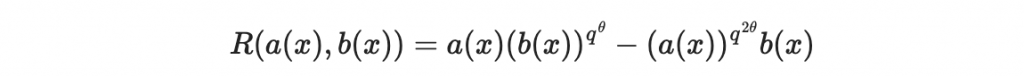
回憶我們在 Day12 所討論的內容，我們知道取 q^theta 次方與 q^2theta 次方都是線性映射。所以 R 函數對 a(x) 來說是線性映射，對 b(x) 來說也是線性映射，我們說 R 函數是一個 a(x) 與 b(x) 的雙線性映射（Bilinear map）

除此之外，當 a(x) 與 b(x) 滿足 b(x) = F(a(x)) 的關係時，R(a(x), b(x)) = 0。

現在，如果 z / w 是一個明文/密文對，那麼

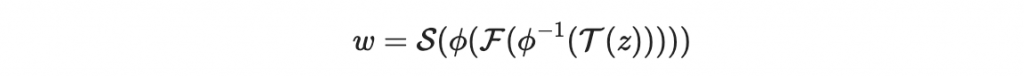
因為 S 以及 phi 都是可逆的

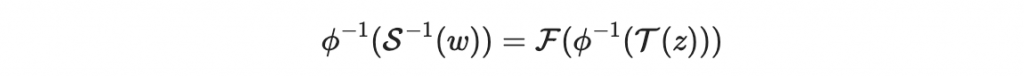
於是

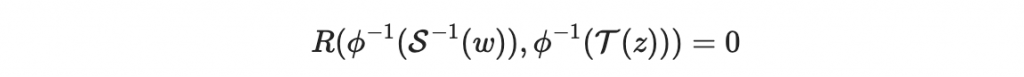
好的，最後的最後。

S 是一個仿射變換，我們可以寫成

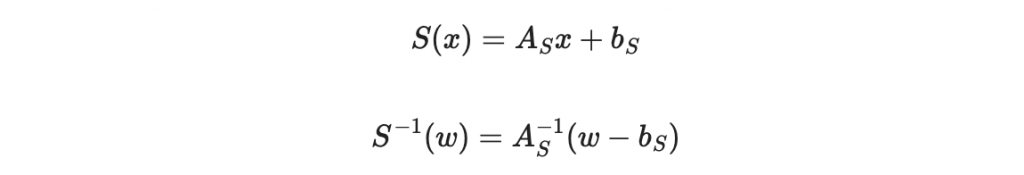
因此 S^(-1)(w) 是一個對變數 w + c 的線性映射，c 是某個常數向量。

T 是一個仿射變換，我們可以寫成

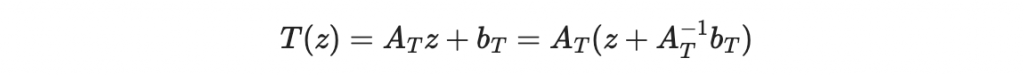
因此 T(z) 是一個對變數 z + d 的線性映射，d 是某個常數向量。

全部合在一起說，意思是以下函數

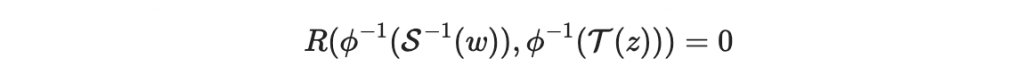
是 w + c 與 z + d 的雙線性映射， c 與 d 都是某個不重要的常數向量。

好！因此我們可以把

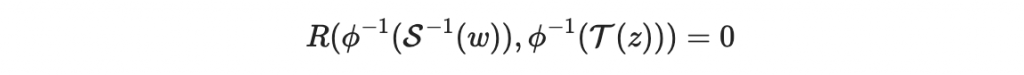
寫成

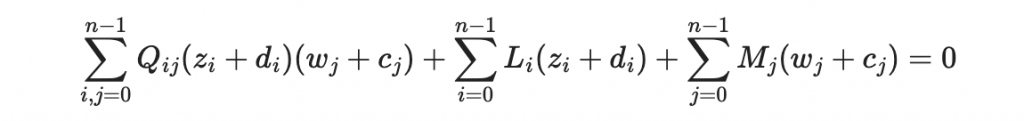
經過乘開與整理後，你可以得到

結論

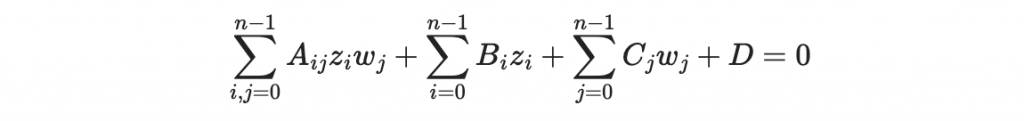
從這裡我們可以得到一個重要結論：在一套正確的 MI 系統之下，所有的明文/密文對將會滿足某些形如以下的方程式：

線性化攻擊

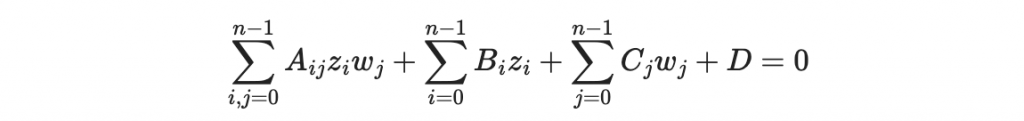
因為上面結論中的方程式有 (n+1)^2 個係數，所以只要我們使用公鑰來生成 (n+1)^2 個明文/密文對，就可以把這些明文/密文對代入

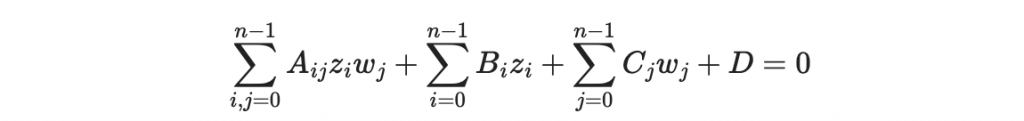
並用高斯消去法解出 A_ij, B_i, C_j, D 等係數。下次我們看到別人傳送的密文 w* 時（專有名詞：挑戰密文 Challenge ciphertext）我們就把 w* 代入上面的線性方程，就可以得到一個變數 z0, z1, ..., z_{n-1} 的線性方程式。

在用高斯消去法解出 A_ij, B_i, C_j, D 等係數時，我們應該會解出不只一組 A_ij, B_i, C_j, D 的解，也就是 z/w 滿足好幾條這樣的線性方程式，這是好事，因為每個線性方程都只提供一個等號，而我們要求解的明文 z 有 n 個變數，最好需要 n 個等號（n 個條件）才能精確求解，

我們待會實作時，就會發現最後真的不一定有 n 個條件可用，但剩下的可能性很少，所以用暴力搜尋法很快就可以得到。

實作破密

首先承襲前幾天的程式碼，不過現在把 n 調整到 20，所以

a = [R(randint(0,1)) for i in range(n)]
print(a)
print(Publishable_Public_Key(a))

我們打算生成 (n+1)^2 個明文密文對，並代入

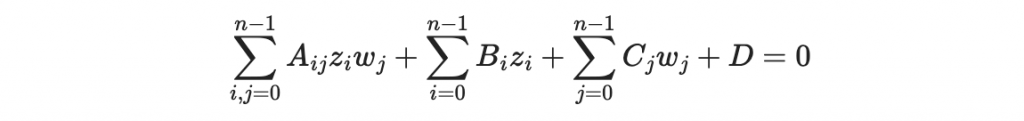
解得 A_ij, B_i, C_j, D。

先生成 (n+1)^2 個明文密文對

# Generate (n+1) plaintext/ciphertext pairs
plaintexts = []
ciphertexts = []
for _ in range((n+1)^2):
    x = [R(randint(0,1)) for i in range(n)]
    plaintexts.append(x)
    ciphertexts.append(Publishable_Public_Key(x))

接著我們把變數 A_ij, B_i, C_j, D 的係數存放在一個矩陣裡，等等會對他做高斯消去法，計算零空間，解得 A_ij, B_i, C_j, D

Linear_System = [[0 for j in range((n+1)^2)] for i in range((n+1)^2)]

for k in range((n+1)^2):
    plaintext = plaintexts[k]
    ciphertext = ciphertexts[k]
    
    for i in range(n):
        for j in range(n):
            Linear_System[k][i*n+j] = plaintext[i]*ciphertext[j]

    for i in range(n):
        Linear_System[k][n^2+i] = plaintext[i]

    for i in range(n):
        Linear_System[k][n^2+n+i] = ciphertext[i]
    
    Linear_System[k][-1] = 1

Linear_System = Matrix(Linear_System)
Linear_System_Coefficients = (Matrix(Linear_System).right_kernel().basis())

print((Linear_System_Coefficients)[0])

# Outputs: (1, 0, ..., 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1)

其中 right_kernel() 就會解出這個矩陣的右零空間，

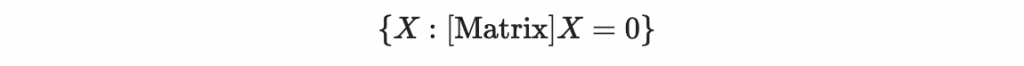
而 basis() 就會告訴你這個解的基底，也就是所有 A_ij, B_i, C_j, D 。

print(len(Linear_System_Coefficients))

# Outputs: 20

我們有 20 條以下的線性方程式

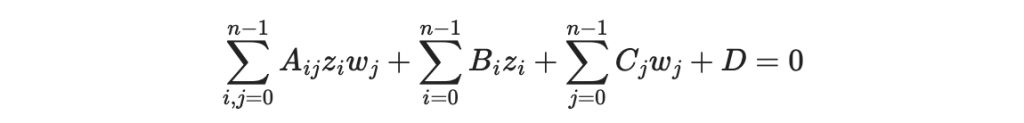
好的，現在生成挑戰明文與挑戰密文：

challenge_plaintext = [R(randint(0,1)) for i in range(n)]
challenge_ciphertext = Publishable_Public_Key(challenge_plaintext)

print("Challenge Plaintext:", challenge_plaintext)
print("Challenge Ciphertext:", challenge_ciphertext)

# Outputs: 
# Challenge Plaintext: [1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
# Challenge Ciphertext: [0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1]

我們接著要解以下方程式，但是是代入挑戰密文後的線性方程

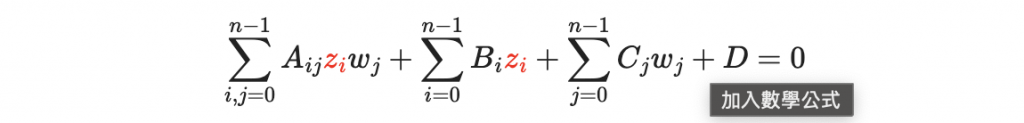
目標就是解出 z_i

先改寫一下：

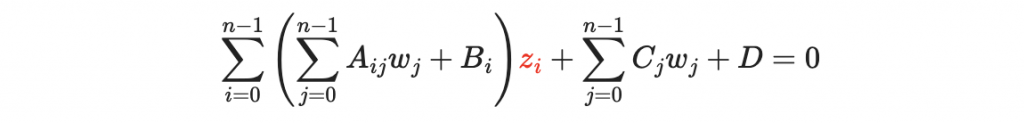
我們會先解出所有形如以下的解

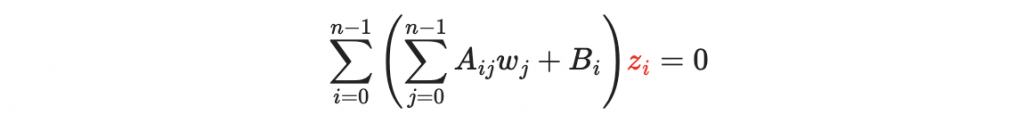
叫做齊次解（homogeneous solutions）記做 h

接著找到某一個真實方程

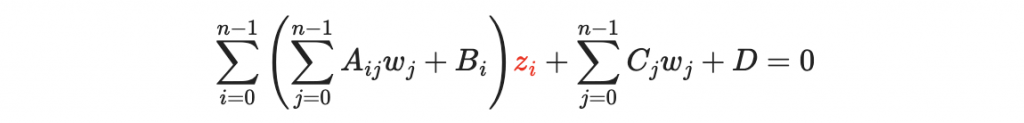
的解，叫做 particular solution ，記做 z。
接著對所有齊次解 h ，

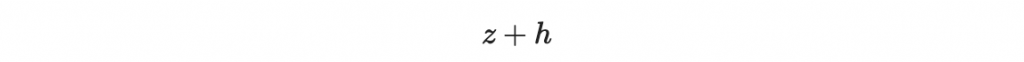
就都會是真實方程的解。只要將所有 h 都跑過一次，並回推看看 z + h 是否等於挑戰密文，如果某個 z + h 的密文等於挑戰密文，則此 z + h 就是挑戰明文。

好！我們來生成

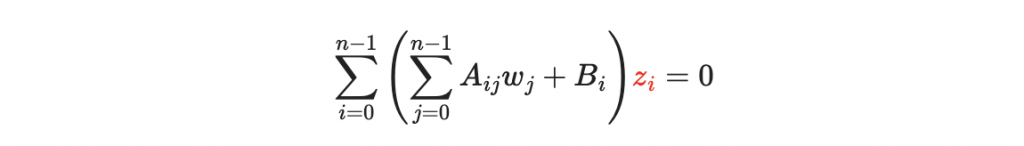
的係數矩陣：

Plaintext_System = [[0 for j in range(n)] for i in range(n)]

for k in range(n):
    for i in range(n):
        coeff = 0
        for j in range(n):
            coeff += Linear_System_Coefficients[k][i*n+j]*challenge_ciphertext[j]
        coeff += Linear_System_Coefficients[k][n^2+i]
        Plaintext_System[k][i] = coeff

Plaintext_System = Matrix(Plaintext_System)
print((Plaintext_System))

# Outputs:
# [0 0 0 1 1 1 1 0 0 0 0 1 1 0 1 1 0 1 0 1]
# [0 1 0 1 1 0 1 0 1 1 1 1 1 0 1 1 1 1 0 0]
# [0 0 0 1 1 0 0 0 0 0 1 0 1 1 1 0 1 0 1 0]
# [0 1 1 1 0 0 0 0 1 0 0 1 0 0 0 0 1 1 0 0]
# [0 1 1 1 0 1 1 0 0 0 0 0 1 0 1 1 0 0 1 1]
# [1 0 0 0 0 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0]
# [1 1 1 0 1 1 0 1 0 1 0 0 0 0 1 1 0 0 1 0]
# [1 1 0 1 1 1 1 0 1 1 1 1 0 0 0 1 0 1 1 0]
# [0 0 0 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 0 1]
# [1 1 1 0 0 1 0 0 0 0 1 0 1 0 0 0 1 0 0 1]
# [1 1 0 1 0 0 0 1 0 1 1 0 0 1 1 1 1 1 1 0]
# [0 1 1 0 0 0 0 1 1 1 0 1 0 0 0 1 0 1 1 0]
# [1 1 0 1 0 0 1 0 0 0 0 1 1 1 1 1 0 1 1 1]
# [0 1 0 1 0 0 1 0 1 0 1 0 1 0 1 1 0 1 0 1]
# [1 1 0 0 0 0 0 1 1 0 1 1 0 0 1 0 1 1 0 0]
# [0 1 0 0 0 1 0 1 0 0 0 0 1 0 1 1 0 1 1 1]
# [0 0 0 1 1 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1]
# [0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 1]
# [0 0 1 1 1 1 0 1 1 0 1 1 1 0 0 1 0 0 0 1]
# [0 0 1 1 1 1 0 1 1 1 0 1 0 1 1 0 1 0 0 0]

找出所有的齊次解

homo_sols = Plaintext_System.right_kernel().list()
print(homo_sols)

# Outputs:
# [(0, 0, 0, 0, 0, 0, 0, 0, 0, ... , 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1)]

接著計算

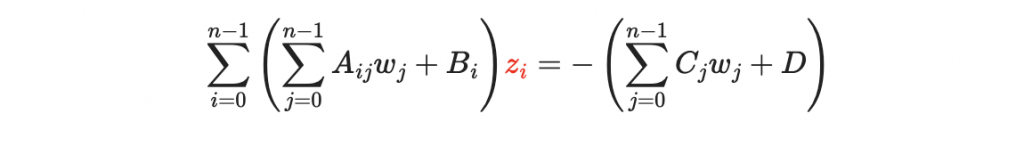
的右手邊

y = [0 for i in range(n)]

for i in range(n):
    coeff = 0
    for j in range(n):
        coeff += Linear_System_Coefficients[i][n^2 + n + j] *challenge_ciphertext[j]
    coeff += Linear_System_Coefficients[i][-1]
    y[i] = -coeff

print(y)

# Outputs:
# [1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1]

找出某個真正的解 z (particular solution)

y = vector(y)
particular_sol = Plaintext_System.solve_right(y)
print(particular_sol)

# Outputs:
# (1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0)

形成所有 z + h

solution_set = []
for homo_sol in homo_sols:
    solution_set.append(homo_sol + particular_sol)

進行非常小範圍的暴力搜尋法

for solution in solution_set:
    if Publishable_Public_Key(solution) == challenge_ciphertext:
        answer = solution
        break

找到了 solution 之後，進行測試

print(answer)
print(answer.list() == challenge_plaintext)

# (1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0)
# True

好！完成破密！

明天開始，我們將討論新的密碼系統如 UOV, Rainbow, MAYO 等等。敬請期待

Takeaway

• 線性化攻擊可以成功，是因為 MI 系統內的中間映射的結構可做成雙線性映射
• 使用 SageMath 實作線性化攻擊

ref
DING, Jintai; GOWER, Jason E.; SCHMIDT, Dieter S. Multivariate public key cryptosystems. Springer Science & Business Media, 2006.