油：Oil
醋：vinegar

系統建構

數學設定

首先生成 v 與 o ，分別叫做醋變量數量、油變量數量，
我們會使用 n 個未知數，n = o + v

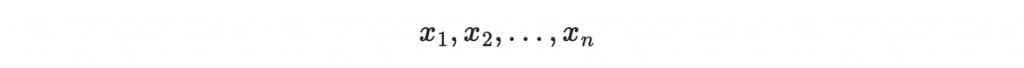
其中前 v 個我們叫做「醋變量」、後 o 個叫做「油變量」

我們把以下的多項式叫做「油醋多項式」

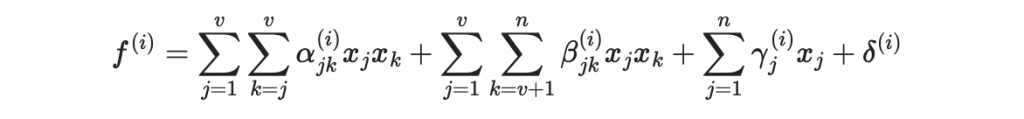
其中的係數通常是隨機生成。注意到第一大項只有醋變量參與，第二大項醋變量油變量都有參與，第三大項是一次項，最後是常數。

關鍵點在於：如果已知 alpha, beta, gamma, delta 、也已知 f^{(i)} 、也已知醋變量的真實數字，則剩餘的方程式是油變量的線性方程式。

系統建構

我們仍然使用雙極構造法，其中的中間映射就是由 o 個形如上述的油醋多項式組成。

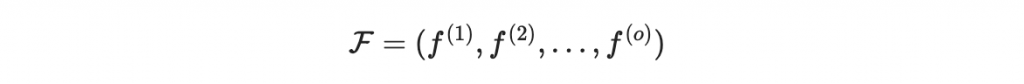
接著注意到，在 F 後面接上一個仿射變換 S 後，出來的 o 個多項式仍然是油醋多項式。那因為我們的 F 本來就是隨機生成，所以接不接 S 無所謂。

根據雙極構造法，我們會再生成一個仿射變換 T。

公鑰為 P(x) = F(T(x))
私鑰為 F(x), T(x)

簽章步驟

簽章者

首先生成公私鑰：就是隨機生成 o 個油醋多項式

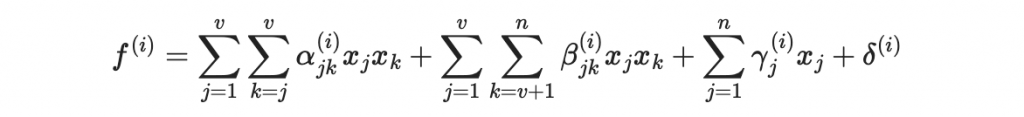
係數都是隨機生成。

接著，把欲簽章的文件 hash 到長度為 o 的數字序列。（如果你不知道什麼是 hash ，你就當作我們要簽章的文件可以壓縮為長度 o 的數字序列，這個壓縮是不可逆的，但每次壓縮結果都一樣）

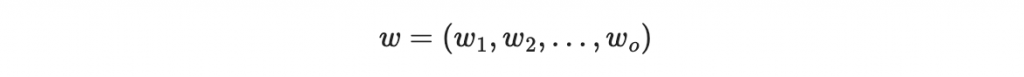
接著，簽章者會計算一個「簽章」sigma 滿足

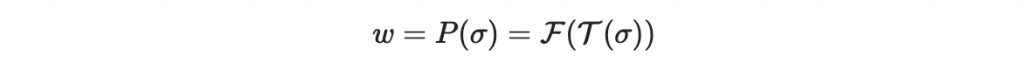
換句話說

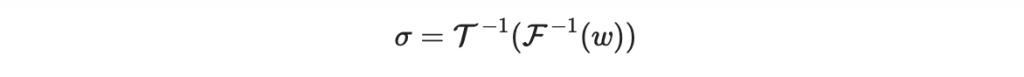
注意到 sigma 是一個長度為 n = v + o 的數字序列。

為了計算這個 sigma，第一步要先計算 F^-1(w)：
隨機生成 v 個數字，代入醋變量。
於是上面的油醋多項式

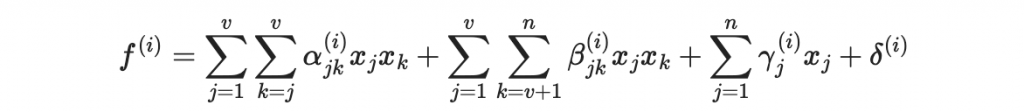
就變成油變量的線性方程式：（紅色是油變量）

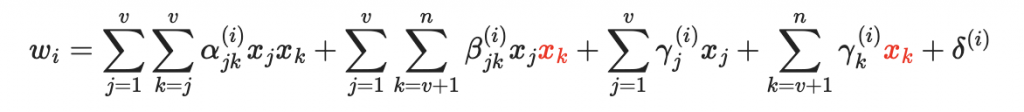
此時，我們有 i = 1, 2, ..., o 共 o 個油變量的線性方程組，這可以用高斯消去法來求解。

此時，如果油變量無解的話，重新生成 v 個醋變量，重新嘗試求解油變量。

如果油變量有解的話，那我們把醋變量跟油變量接在一起

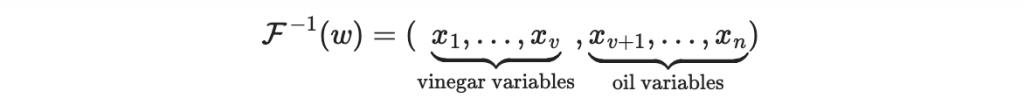
下一步，計算

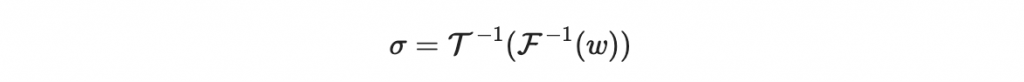
於是你就有了簽章 sigma

驗章者

把 sigma 代入公鑰 P ，看看有沒有等於 w 。Done

程式實作

我們就按照剛剛的順序來用 SageMath 實作，因為過程中沒有涉及什麼高難度的多項式商環，我們把參數用的大一些些😀

首先我們設定所有數字所在的整數環：Z / 79 Z

q = 79
R = quotient(ZZ, q*ZZ)
print(R)

# Outputs:
# Ring of integers modulo 79

使用 19 個醋變數、21 個油變數

v = 19
o = 21
n = o + v

仿射變換

# Function to generate a random affine map
def RandomAffineMapGenerator(n, R):
    while True:
        # Generate a random n x n matrix for the linear part of the affine map
        A = random_matrix(R, n, n)

        # Check if A is invertible
        if A.is_invertible():
            break

    # Generate a random n-dimensional vector for the translation part
    b = random_vector(R, n)

    # Define the nested affine map function
    def AffineMap(v):
        v = vector(v)
        v = A * v + b
        return v.list()

    # Define the inverse affine map function
    def InverseMap(v):
        v = vector(v)
        v = A.inverse() * (v - b)
        return v.list()

    # Return the affine map function, the inverse map function, and the components
    return AffineMap, InverseMap, A, b


T,T_inv,A,b = RandomAffineMapGenerator(n,R)

生成 o 個油醋多項式：

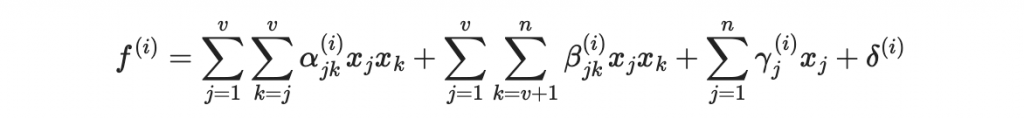
其中我們把 alpha 係數存在 VV 矩陣內，beta 係數在 VO，gamma 係數在 L

VVs = []
VOs = []
Ls = []
Ds = []

for _ in range(o):
    
    # Generate a random v x v upper triangular matrix
    VV = random_matrix(R, v, v)

    for i in range(v):
        for j in range(i):
            VV[i, j] = 0


    # Generate a random v x o matrix
    VO = random_matrix(R, v, o)

    # Generate a random 1 x n matrix
    L = random_matrix(R, 1, n)

    # Generate a random constant term
    D = R.random_element()

    VVs.append(VV)
    VOs.append(VO)
    Ls.append(L)
    Ds.append(D)


print(VVs[0],"\n")
print(VOs[0],"\n")
print(Ls[0] ,"\n")
print(Ds[0] ,"\n")

# Output:
# (two matrices and a row matrix and a constant term)

現在開始進行簽章

# Sign a message
# 我們就假裝要簽章的文件就是隨機的
w = [randint(0, q-1) for _ in range(o)]
print(w)

# Outputs: 
# [50, 14, 32,  ..., 34, 74, 26, 5]

先計算

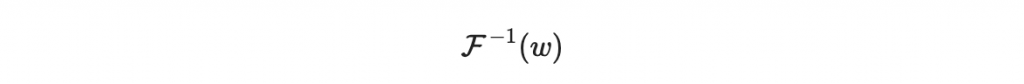
生成隨機的醋變量值

vinegar_variables = [randint(0, q-1) for _ in range(v)]
print("Vinegar variables: ", vinegar_variables)

# Outputs:
# Vinegar variables:  [3, 31, ..., 25, 41, 77, 57]

將醋變量值代入油醋多項式後，會剩下油變量的線性方程組

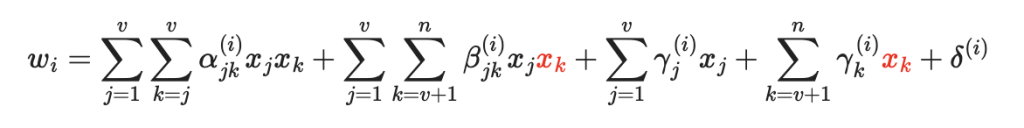
改寫一下：

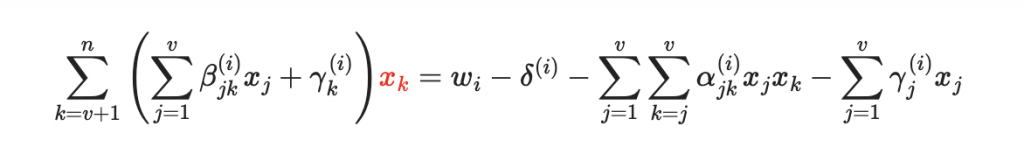
現在我們生成這部分的係數矩陣

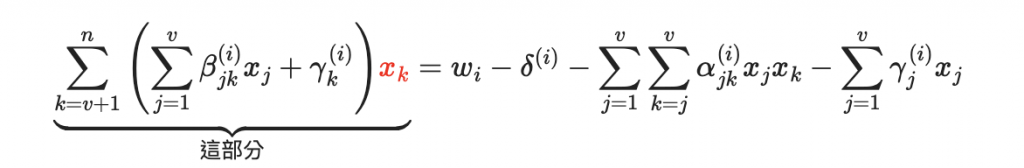
Linear_System = [[0 for i in range(o)] for k in range(o)]

for i in range(o):
    for k in range(v,n):

        coeff = 0
        for j in range(v):
            coeff += VOs[i][j, k-v] * vinegar_variables[j]

        coeff += Ls[i][0, k]

        Linear_System[i][k-v] = coeff

印出矩陣

Linear_System = Matrix(Linear_System)
print("Linear System:\n\n"+str(Linear_System))

# Outputs:
# (A big matrix)

接著計算右側的常數向量

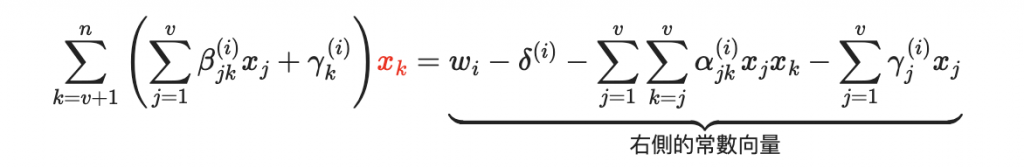
# Calculate the constant terms

constant_terms = [0 for _ in range(o)]

for i in range(o):
    constant_terms[i] = w[i] - Ds[i]


    vinegar_variables_vector = Matrix([[vinegar_variables[j]] for j in range(v)]) # column vector
    num = vinegar_variables_vector.T * VVs[i] * vinegar_variables_vector

    constant_terms[i] -= num[0,0]


    for j in range(v):
        constant_terms[i] -= Ls[i][0, j] * vinegar_variables[j]
 

constant_terms = vector(constant_terms)
print("Constant terms: ", constant_terms)

# Outputs:
# Constant terms:  Constant terms:  (25, 69, 47, ..., 31, 22, 68, 21)

現在嘗試解線性方程

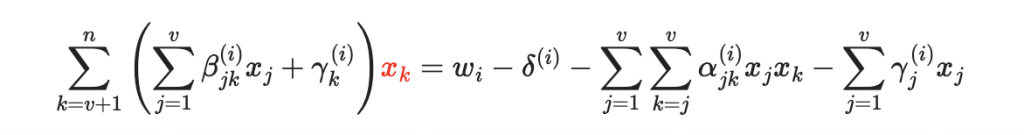
try:
    solution = Linear_System.solve_right(constant_terms)
except ValueError as e:
    print(f"Please re-select the vinegar variables: {e}")


print(solution)

# Outputs:
# (71, 48, 46, 18, ... 3, 15, 76, 72)

最後，計算

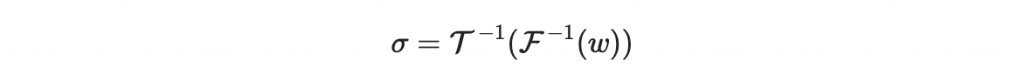
all_variables = vinegar_variables + solution.list()
signature =T_inv(all_variables)
print("Signature: ", signature)


# Outputs:
# Signature:  [57, 74, 48, 18, ..., 67, 6, 69, 25]

好！來驗章！
我們把中間映射定義好

def Central_map(all_variables):
    result = []
    for i in range(o):

        result.append(Ds[i])

        for j in range(v):
            for k in range(j, v):
                result[i] += VVs[i][j, k] * all_variables[j] * all_variables[k]

        for j in range(v):
            for k in range(v, n):
                result[i] += VOs[i][j, k-v] * all_variables[j] * all_variables[k]

        for j in range(0, n):
            result[i] += Ls[i][0, j] * all_variables[j]

    return result

然後計算 P(x) ，看看有沒有等於 w

signature = T(signature)
print(Central_map(signature))
print(Central_map(signature) == w)

# Outputs:
# [1, 2, 7, 59, ... , 37, 34, 49, 73]
# True

（你可以看到，與之前 MI 的介紹一樣，這裡的公鑰係數需要被計算出來，但是那已經偏離此文重點，故省略之）

好！明天我們來看彩虹簽章！

Takeaway

• 了解不平衡油醋簽章的步驟
• 何謂油醋多項式？
• 油醋多項式的結構如何幫助我們計算中間映射的反映射？

ref
DING, Jintai; GOWER, Jason E.; SCHMIDT, Dieter S. Multivariate public key cryptosystems. Springer Science & Business Media, 2006.