今天我們來介紹彩虹簽章！

回顧昨天油醋醬簽章

首先，隨機生成中間映射，中間映射由油醋多項式構成：

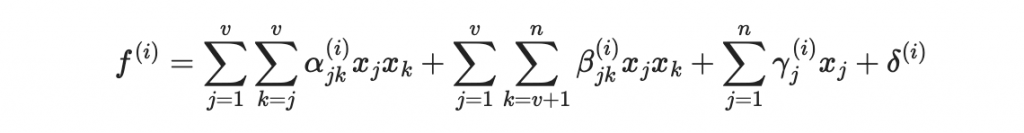
在簽章的時候，我們會隨機給醋變量 x1, ..., x_v 一組隨機值，於是未知數只剩下紅色的油變量

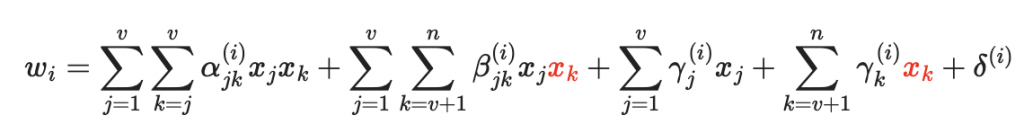
這是一個對油變量的線性方程式，因此我們有很高的機會求解，若無解的話，我們重新生成醋變量的值，若無限多組解，那我們可以隨機挑一個。

層次化的中間映射

好，簡單來說，彩虹簽章就是很多層的油醋簽章組合重疊而成。

令

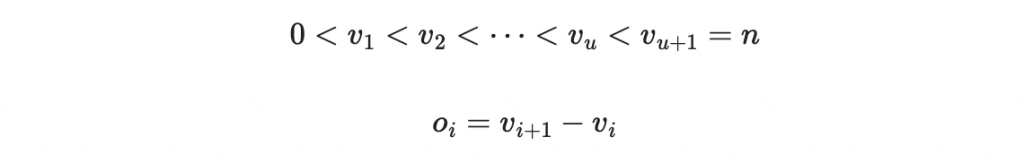
一共有 n 個變量

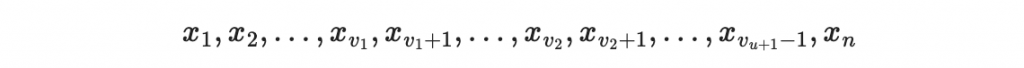
請想像一下：假設一開始我們把前 v1 個變量先當作醋變量，並隨機生成他的值。把第 v1 + 1 到 v2 個變量先當作油變量，那我們可以透過 o1 個形如以下的 v1-o1 油醋多項式中求到這 o1 個油變量的值

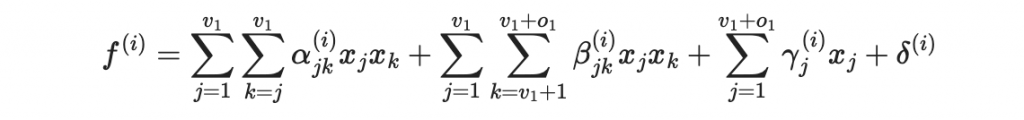
到此為止我們一共知道了 v2 = v1 + o1 個變量的值。接著把接下來的 v2+1 到 v3 個變量當作油變量，那我們可以透過 o2 個形如以下的 v2-o2 油醋多項式中求到這 o2 個油變量的值

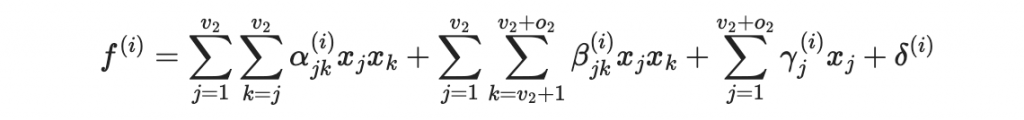
到此為止我們一共知道了 v3 = v2 + o2 個變量的值。

以此類推，最終就可以求到所有的 x 變量。在這過程中，各層分別需要用到 o1 + o2 + ... + o_u = n - v1 個油醋多項式。

彩虹簽章

雙極構造法

生成兩個隨機的可逆仿射變換 S 與 T
中間映射為 F ，分別由 o1 個 v1-o1 油醋多項式、o2 個 v2-o2 油醋多項式、......、o_u 個 v_u-o_u 油醋多項式。一共有 n - v1 個油醋多項式。

私鑰為 S, F, T
公鑰為 P(x) = S(F(T(x)))

S 與 T，分別是作用在 n-v1 維與 n 維空間上。

簽章過程

好！我們來看簽章過程！

假設我們要簽章的文件經過 hash 函數後是

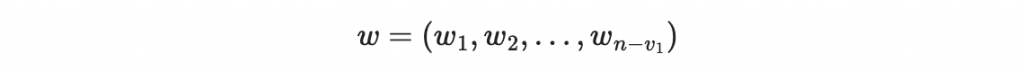
這是一個 n - v1 維度的向量。

首先我們會先計算

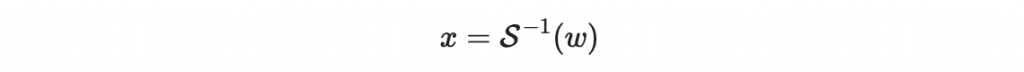
其中 x 是 n - v1 維度的向量

接著計算

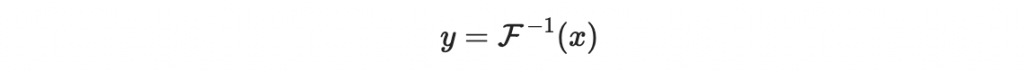
這個部分是透過我們第二節「層次化的中間映射」中介紹的方法計算得到。其中 y 是 n 維度的向量。

最後計算

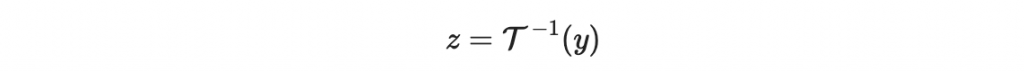
其中 z 是 n 維度的向量。

發送簽名

驗章過程

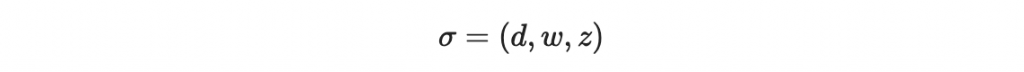
計算 P(z) 並檢查：

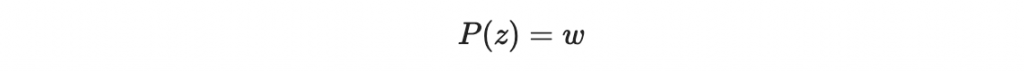
若以上等式成立，則簽名為有效簽名。Done

Takeaway

• 何謂層次化的中間映射？

層次化的中間映射是將變量分層，逐層求解油變量的方法，每一層利用已知的醋變量，解決對應的油醋多項式方程組。

後記

道歉啟事：今天收到兵單，心情極度鬱卒，因此沒有把程式寫好。（你可以在這裡看到月亮巨蟹人是有多容易被心情影響工作......）

ref
DING, Jintai; GOWER, Jason E.; SCHMIDT, Dieter S. Multivariate public key cryptosystems. Springer Science & Business Media, 2006.