在過去幾天中，我們深入探討了多元二次多項式系統及其在密碼學中的應用，這類系統以其計算上的難度成為後量子時代密碼學的重要候選。今天我們來做個小結

多元二次多項式系統回顧

多元二次多項式系統（Multivariate Quadratic Polynomial System, MQ）是一組由多個二次多項式方程組成的系統。這些多項式的通式可以表達為：

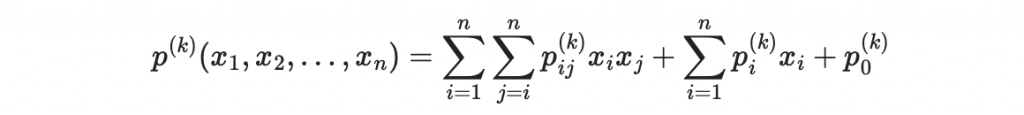
矩陣表示法可以是：

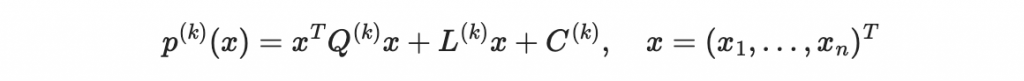
其中，x_1, x_2, ..., x_n 是變量，p_{ij}^{(k)} 是二次項的係數，p_i^{(k)} 是一次項的係數，p_0^{(k)} 是常數項。這些多項式的非線性結構使得從輸出值反推出輸入變量變得極具挑戰性。

對於任意給定的 x_1, x_2, ..., x_n，計算這些多項式的輸出是一個簡單的問題；然而，從輸出反推出 x_1, x_2, ..., x_n 則是一個困難的問題，這正是多元二次多項式系統在密碼學中具有價值的原因——這種反演難度能有效防止破解。

計算困難性與密碼學應用

多元二次多項式系統的反函數求解是非常困難，目前尚無有效的算法能在多項式時間內求解這類系統的反函數。因此，這類系統非常適合應用於構造公鑰加密系統和數字簽章系統。

在一個典型的公鑰加密系統中，公開密鑰是多個由這類多項式系統生成的方程，解密若想要破解，則需要求解這些二次方程組。

加密者可以通過快速計算多項式的方式加密訊息，而解密者則需要使用私鑰進行高效求解，這正是多元二次多項式系統的基本思路。

雙極構造法

為了進一步提高系統的安全性，我們引入了雙極構造法。該方法通過生成兩個可逆仿射變換 T 和 S，以及一個“易於求反函數”的多元二次多項式系統 F，來生成加密和解密密鑰。

具體的，雙極構造法如下：

1. 生成仿射變換：生成兩個可逆仿射變換 T 和 S，分別作用於明文和密文空間。
2. 生成簡單的中心映射：構造一個「容易計算反函數」的中心多項式系統 F。這個系統通常是設計用來在解密過程中快速求解的簡單映射。
3. 生成公鑰和私鑰：
   • 公鑰為：P(x) = S(F(T(x)))，其中經過前後兩次仿射變換後的多項式系統變得非常複雜。
   • 私鑰為：T, S, F

通過這樣的變換，公開的多項式系統係數看似隨機，增加了破解難度。即便攻擊者知道公鑰，也難以推導出對應的私鑰，從而保證了系統的安全性。

Matsumoto-Imai 系統

在多元二次多項式系統中，Matsumoto-Imai 系統是一個著名的實例。該系統的核心思想是生成一個中心映射

• 中心映射的設計：這個系統的 F(x) 映射可以通過簡單的指數運算進行反演，極大地提升了解密效率。
• 安全性（雙極構造法）：該系統的安全性主要來自仿射變換 T 和 S，使得攻擊者難以從公鑰推出密鑰。

HFE 系統（隱藏域方程） 

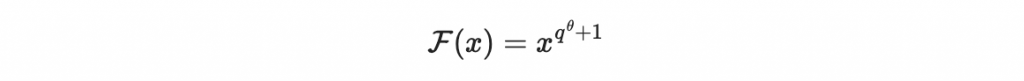
HFE 系統（Hidden Field Equations）是另一個基於多元二次多項式系統的後量子密碼系統。

HFE 系統利用有限域上的多項式求解問題作為其安全基礎，並通過映射到隱藏域來進一步增強其安全性。
- 中心映射的設計：HFE 系統的核心映射形如

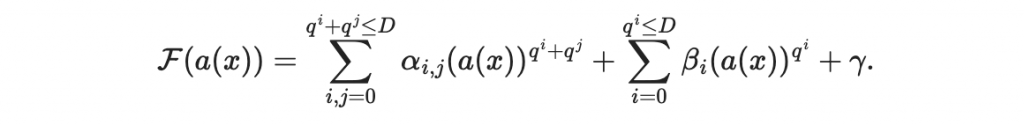
其中 q 是有限域的基數（我在該文章中使用 q = 2），i 和 j 是指數。這樣的設計使得在隱藏域中的映射具有線性結構，但在公開域中卻呈現非線性，從而難以破解。 
- 安全性（雙極構造法）：HFE 系統的安全性來自於將求解問題隱藏在一個更複雜的代數結構中，使得即使攻擊者知道公鑰，也難以推導出私鑰。

UOV 系統

另一個重要的多元二次多項式系統是 UOV 系統（不平衡油醋系統，Unbalanced Oil and Vinegar）。UOV 系統的獨特之處在於它的多項式結構中將變量分為兩類：油變量和醋變量。通過隨機生成的醋變量，UOV 系統能夠將剩餘的多項式轉換為油變量的線性方程組，從而使得油變量的求解變得簡單。

UOV 系統的構建步驟

1. 分配變量：將變量分為油變量和醋變量。
2. 構建多項式系統：油變量和醋變量組合成多元二次多項式，每一個多項式的結構分別對應於油變量和醋變量之間的交互作用。這裡的多項式都是形如以下的油醋多項式：

3. 簽章過程：在生成簽章時，隨機生成醋變量並代入多項式系統中，剩下的油變量通過求解線性方程組獲得。

彩虹簽章系統

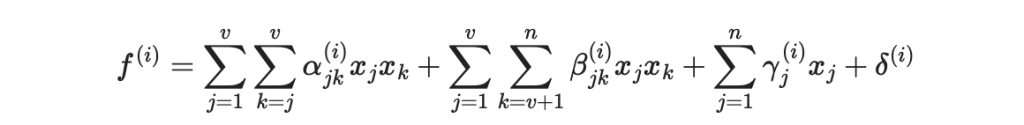
在我們討論的密碼系統中，彩虹簽章系統（Rainbow Signatures）是 UOV 系統的多層次擴展。

彩虹簽章的層次結構

彩虹簽章將變量分為多層，每一層的變量都分為油變量和醋變量。隨著每層的推進，逐步求解變量，最終得到整體的簽章：

1. 第一層求解：隨機選擇第一層的醋變量，解出油變量。
2. 第二層求解：將第一層的所有變量當作已知，再進一步解第二層的油變量。
3. 多層疊加：以此類推，直到求出最終的簽章。

彩虹簽章系統通過這種層次化的結構，可以提高簽章的安全性，並且能夠有效抵禦傳統攻擊。同時，該系統的設計使得簽章和驗章過程仍然保持高效。（因為你唯一做的事情就是高斯消去）

結論

多元二次多項式系統作為後量子密碼學中的關鍵領域，展現出強大的潛力。這些系統利用二次方程的求解困難性，並通過仿射變換和特殊結構（如雙極構造法、油醋變量、彩虹層次）進一步增強了其安全性和實用性。隨著量子計算技術的進步，多元二次多項式密碼系統很可能會成為新一代密碼標準的一部分，在保護未來信息安全中扮演重要角色。