不知道你會不會覺得,昨天介紹的解法中,第一步「不斷迭代 mean prompt 以優化這個 prompt」,需要每做1個或n個對 token 的操作,就上傳到 leaderboard 上觀察結果以決定下一步要怎麼做,這個也太麻煩了吧!
尤其 Leaderboard 有限制每天繳交次數,這樣是要花多少時間才可以優化好呀🤯!
今天首先要介紹第八名的解法,我認為和第七名有點像,都是找到一個 mean prompt 之後,使用 LLM 幫每一題預測一個(或兩個)可能的 rewrite prompt,再和前面找到的 mean prompt 以某種方式結合,當成該題的答案。
只是昨天介紹的第七名解法,第一步要不斷和 LB 確認就算了,後面找到最佳 embedding 之後還要去解碼才能得到最終答案,過程好玩是好玩,但是複雜度有點高。
今天要介紹的第八名就簡化且自動化了第七名的流程,我們一起來看看吧!
第八名1的解法整體可以分成兩個步驟:Mean prompt training 與減少訓練集的誤差-Reducing bias in training dataset。
有別於每次對初始 mean prompt 做一個 token operation 就要上傳到 LB 檢查看看效果有沒有變好,他們找到一個公開的Rewrite Prompt資料集(請參考:2)一共有近九千多筆 prompt。
他們先假設這個 prompt dataset 會和 Host 的 test prompt dataset 很像,所以他們一樣透過在 initial prompt 隨機插入、刪除、取代 token 創造新的 prompt 後,評估新生出來的 prompt 跟這個公開dataset 的 prompt 轉換出的 embedding similarity 有沒有提高,如果有的話就用這個新找出來的 prompt 繼續迭代下去找。
最終停止時,就可以找到一個和這個 training prompt dataset 的相似度很高的一個 prompt,我們就用它當作要提交的 mean prompt。
為了幫助理解,我們一樣重構他的 code 來解釋(原始版本請參考3):
先定義一些常用的 function:
embedder = SentenceTransformer("/kaggle/input/sentence-t5-base-hf/sentence-t5-base")
def embed_text(texts: Iterable[str]) -> np.ndarray:
return embedder.encode(texts)
def cosine_cube_similarity(emb1: np.ndarray, emb2: np.ndarray) -> np.ndarray:
return cosine_similarity(emb1, emb2) ** 3
# prompts_embs 儲存訓練集所有 prompt 的向量
def transition_fn(prompt_list: list[str], index: int):
prompt_candidates = []
for word in words:
prompt_candidate_words = prompt_list.copy()
prompt_candidate_words.insert(index, word)
prompt_candidates.append(prompt_candidate_words)
embs_candidates = embed_text([concat_prompt(x) for x in prompt_candidates])
similarities = cosine_cube_similarity(embs_candidates, prompts_embs).mean(axis=1)
return list(zip(prompt_candidates, similarities))
class BeamSearch:
def __init__(self, beam_width, token_limit=128, insert=True):
self.beam_width = beam_width
self.token_limit = token_limit
self.insert = insert
def search(self, initial_state, transition_fn, max_length, initial_index):
beam = [(0, initial_state)]
for i in range(max_length):
new_beam = []
for score, sequence in beam:
candidates = transition_fn(sequence, initial_index + i)
for new_sequence, candidate_score in candidates:
new_score = candidate_score
if len(new_beam) < self.beam_width or new_score > new_beam[0][0]:
heapq.heappush(new_beam, (new_score, new_sequence))
if len(new_beam) > self.beam_width:
heapq.heappop(new_beam)
beam = new_beam
return beam
這段代碼會逐步生成新的prompt,並通過 transition_fn 計算這些新的 prompt 與 trainset 裡的 prompt 的相似度。最終保留得分最高的新 candidate prompt,然後下一輪就從這個 prompt 開始生成新的 prompt,重複該過程。
但現在問題來了,他們一開始的假設:「這個 prompt dataset 會和 host 的 test prompt dataset 很像」,所以才藉由產生和這個 trainset prompt 相似度很高的新 prompt 當成答案,試圖在 LB 上也拿高分。
但經過驗證,這顯然並不成立。
因為他們把幾個找到的 mean prompt 提交後,發現這些 prompt 雖然在本地和 trainset 的相似度很高,但在 LB 得到的分數卻差異很大,有高有低。
所以他們下一步要做的,就是盡量減少 trainset 和 testset 的 bias。
透過前面操作多次 Beam Search,我們可以得到多個 mean prompt,紀錄每個 mean_prompt 在 LB 取得到分數後,我們可以得到一個 (LB score, mean_prompt) 的列表:
scores = [
# 70 more mean prompts
[0.60, "Improve the text to this."],
[0.59, "rewrite this text tothepoint humanoid about around towards takes accompanying"],
[0.59, "rewrite this text conveying human ensue somehow portrayal one further"],
[0.59, "rewrite it make thee o e be how this described the text ideas lie plane ultimate"],
[0.58, "Improve the text to this. Rewrite this text using this style."],
[0.56, "Improve essay to this. rewrite this text using this style."]
]
有些分數高有些分數低,可能是因為 training data 和 testing data 的 bias。
那如果我們用某種方法剔除掉 training data 中和 testing data 差異較大的 prompt,再用剩下的 prompt 迭代做 beam search,是不是這樣產生的 mean prompt 就會比較靠近 testing data 中的 prompts 在 embedding space 的中心點呢?
可是我們又無法得知真實的 prompt,又該怎麼踢掉那些不像真實 testing prompt 的 training prompt 呢?
我們可以利用目前唯一和 testing data 有關係的東西,也就是剛剛建立的 score list,裡面存放剛剛找到的那些 mean prompt text 以及這些 mean prompt 得到的 LB 分數。
他的想法是這樣,我們用下圖來解釋:
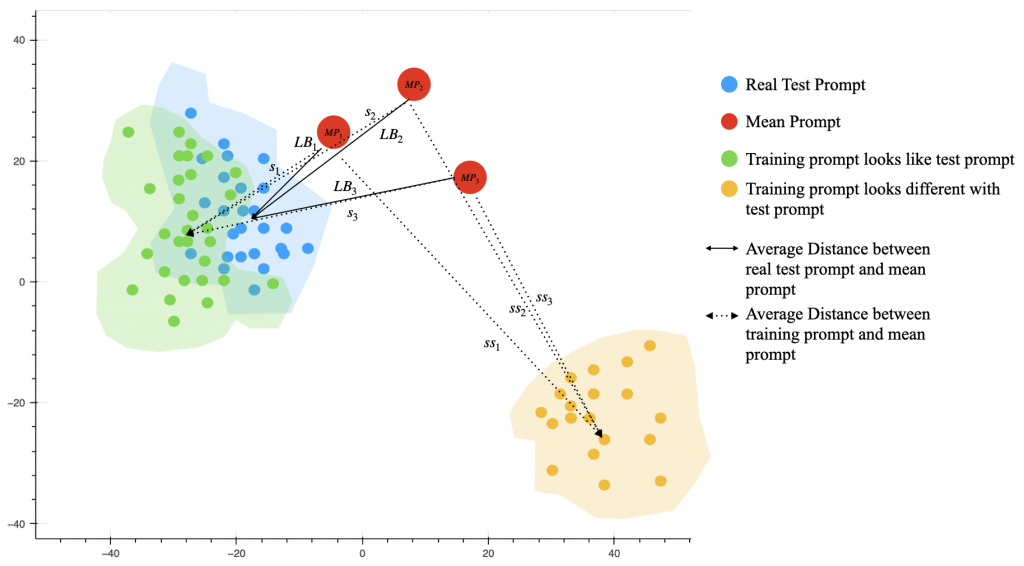
藍色點點是我們不知道的 testing prompt 在向量空間中的分佈,每個 mean prompt 所得到的 LB 分數,其實就是紅點(mean prompt) 和每個藍點(真實的 testing prompt) 的平均餘弦距離。
在圖上可以看到 LB_1, LB_2, LB_3 其實就是每個 mean prompt 和所有 test prompt 的平均距離,同時也就是 leaderboard 上的分數。
假設現在 training data 中,有一群 prompt 非常像 testing prompt,這些 prompt 就是圖上的綠色點點,他們在向量空間上的分佈會非常靠近真實的 testing prompt。
那每個 mean prompt 紅點與這些綠點的平均餘弦距離,應該也會很像該個 mean prompt 得到的 LB 分數。也就是說每個 mean prompt 和這群 training prompt 得到的平均距離,就是 s_1, s_2, s_3,也會非常像 LB1, LB2 和 LB3。
所以如果我們把這些 s_1, s_2, s_3, ..., s_n 和 LB_1, LB_2, LB_3, ..., LB_n 這些分數各自存到一個 list:
S = [s_1, s_2, s_3, ..., s_n]
L = [LB_1, LB_2, LB_3, ..., LB_n]
理想情況下, training prompt (綠色點點)和 test prompt (藍色點點)在空間上的距離非常近,最好的情況是 S ~= L,那計算 cosine_similarity(S, L),就會近似 1。
反之如果有一群 training prompt 離真實 testing prompt 的分佈非常遠,例如圖上的黃色點點,那計算出來的:
SS = [ss1, ss2, ss3, ..., ssn]
similarity{(L, SS)} = cosinesimilarity(L, SS)
這個 similarity 就會極低。
對那些和 L 的 similarity 很高的 training prompt,我們就保留這群 prompt,之後再從這些 bias 更小的 training prompt 去產生新的 mean prompt,進而提高 performance。
我們上代碼會更容易懂:
best_prompts_ids = []
best_score = 0
iteration = 0
while True:
sample_ids = random.sample(range(len(all_prompts_embs)), 10)
candidate_prompts_ids = best_prompts_ids + sample_ids
candidate_scores = (cosine_similarity(lb_prompts_embs, all_prompts_embs[candidate_prompts_ids, :]) ** 3).mean(axis=1).reshape(1, -1)
cos_score = cosine_similarity(candidate_scores, lb_scores)[0][0]
if cos_score > best_score:
best_score = cos_score
best_prompts_ids = candidate_prompts_ids
iteration += 1
這段代碼每次迭代從 training prompt隨機選取 10 個candidate prompt,並計算它們與mean prompt的相似度。如果這批提示詞的得分超過當前最佳得分,則更新提示集合
重點在這兩行:
candidate_scores = (cosine_similarity(lb_prompts_embs, prompts_embs[candidate_prompts_ids, :]) ** 3).mean(axis=1).reshape(1, -1)
這行代碼的目的是計算candidate prompt與mean prompt嵌入之間的相似度分數。
接下來執行:
cos_score = cosine_similarity(candidate_scores, lb_scores)[0][0]
lb_score 是 mean prompt 得到的 leaderboard 分數。
這段 code 在計算什麼?其實就是在算上面提到的 cosine_similarity(L, s) 或是 cisine_similarity(L, ss) 的數值。
如果算出來的 cos_score 比當前的 best_score 高分,那我們就保留這次從 training prompt 隨機挑選出來的這 10 筆 prompt,因為我們認為這些 prompt 和 testing data 之間的差距會比較小。
有了這些新產生出來的 best candidate training prompt 之後,我們再對這些 prompt 執行第一步的 "Mean Prompt Training",反覆執行,就可以找到更好的 mean prompt 了!
好聰明的作法!!
另外他們發現使用 pretrained 好的開源LLM,針對每一題預測可能的 rewrite prompt後,直接append在預先優化好的 mean prompt 後面,又可以帶來些微提升。
昨天是根據 llm 預測的兩個可能的 rewrite prompt,轉成 embedding 再和 mean prompt embedding 做加權產生新的向量,最後再把這個新向量 decode;今天第八名的作法就沒那麼複雜了,直接把llm預測出的文字接在後面就好了。
所以說,第八名的解法很像第七名的簡化版~
我們來看看兩者最終的分數差異:
| Solution | LB |
|---|---|
| 7th | 0.7037 |
| 8th | 0.7026 |
只差了 0.1%。
再統計一下 leaderboard 上金牌區分數的標準差,大概是1.1% 左右,第七名和第八名的分差遠低於標準差,所以兩者之間真的是很微小的差距,但是兩種方法需要的算力卻差滿多的。
今天的解法說明就先到這邊,我們明天見!
謝謝讀到最後的你,希望你會覺得有趣!
如果喜歡這系列,別忘了按下訂閱,才不會錯過最新更新,也可以按讚給我鼓勵唷!
如果有任何回饋和建議,歡迎在留言區和我說✨✨
(Kaggle - LLM Prompt Recovery 解法分享系列)
