Hash 函數

Hash 函數是一種將任意長度的輸入轉換為固定長度輸出的算法，輸出被稱為哈希值（hash value）。好的哈希函數具有以下特性：

• 不可逆性：給定輸出，幾乎不可能反推出輸入。
• 抗碰撞性：幾乎不可能找到兩個不同的輸入產生相同的輸出（即哈希碰撞）。
• 高效性：計算哈希值的時間應該非常快速。

常見的 Hash 函數包括 SHA-256 和 SHA-3，它們在現代密碼學中有著廣泛應用。

讓我們試著使用 Python 來生成 SHA-256 和 SHA-3 的哈希值，你可以將自己的訊息插入進去，看看會產生什麼樣的哈希值。

import hashlib

# 生成 SHA-256 哈希值
message = b"Hello, post-quantum cryptography!"
sha256_hash = hashlib.sha256(message).hexdigest()
print("SHA-256:", sha256_hash)

# 生成 SHA-3 哈希值
sha3_hash = hashlib.sha3_256(message).hexdigest()
print("SHA-3:", sha3_hash)

# Outputs:
# SHA-256: 7ebe72ee56fed16180fd75d263d247f2891e3f1939917016aee2491424269de5
# SHA-3: 9d7192c7e7c661309976e09aa35ef9c792c05be02257387657a23b5f73676adb

量子演算法對 hash 函數的威脅

在量子計算的背景下，Grover's Algorithm 能夠加速暴力破解哈希函數。傳統暴力攻擊的複雜度是 O(2^n)，而使用 Grover's Algorithm，複雜度下降到 O(2^{n/2})。這意味著如果使用 256 位的哈希函數，在量子電腦下的安全性相當於只有 128 位。但也不必太過擔心，只要把安全參數增加一倍即可擁有與之前一樣的安全性

LD-OTS 一次性簽名方案

密鑰生成

對於要簽章的訊息 m 我們會對 m 的每一個位元生成私鑰，一共 2m 個私鑰：

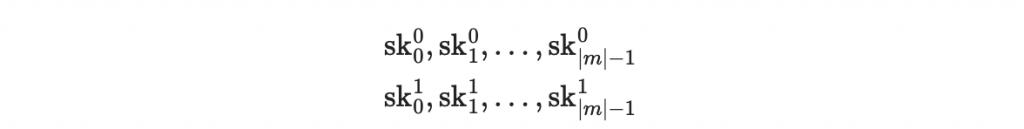
然後使用 hash 函數（這裡使用 SHA-256）生成公鑰：

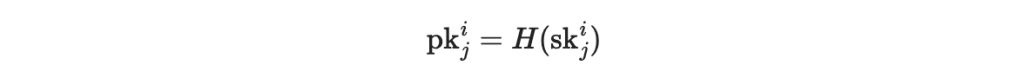
於是我們有 2m 個公鑰：

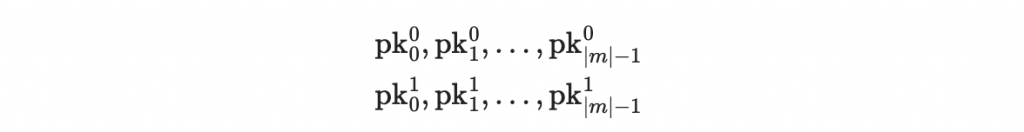
因為我們使用 SHA-256 ，所以我們假設每一個私鑰 sk^{i}_{j} 都是 256 位元，然後每個公鑰 pk^{i}_{j}也會是 256 位元。

簽章

現在我們將 m 表示為二進位字串

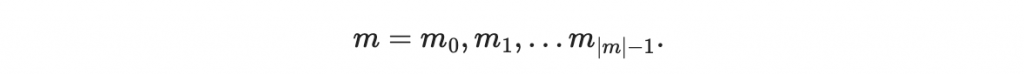
對於每一個位元 m_i 如果 m_i = 0 則該位元的簽章為 sk^{0}_{i}；如果 m_i = 1 則該位元的簽章為 sk^{1}_{i}

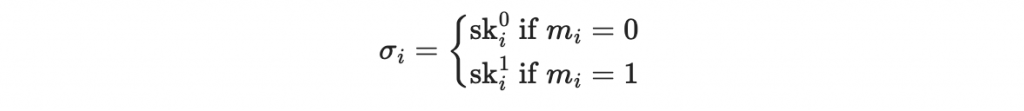
於是就可以做出簽章：

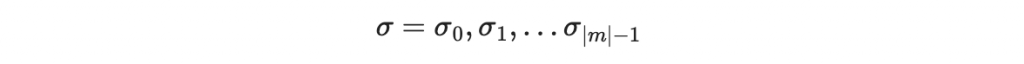
同時，一個完整的簽章還需附上本來的文件 m 以及公鑰

驗章

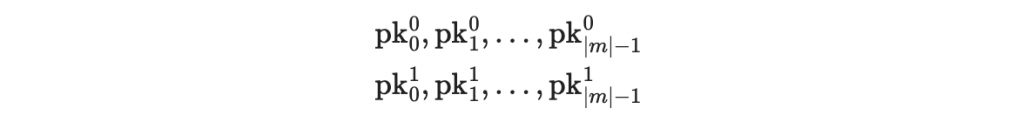
收到簽章、文件、以及公鑰後，開始進行驗章：

一樣看到 m 的二進位字串

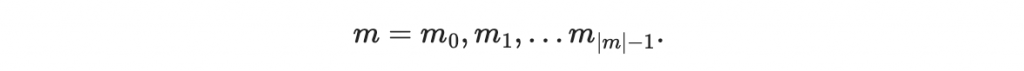
我們逐位元進行驗章。

如果 m_i 等於 0 則查看是否

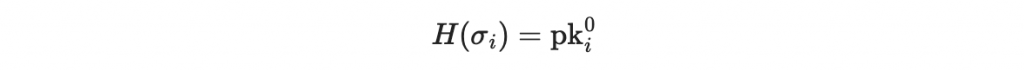
如果 m_i 等於 1 則查看是否

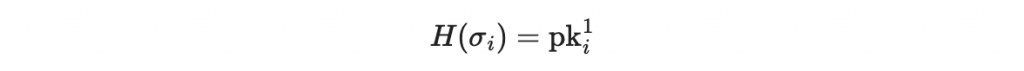
若每個位元都檢查為有效簽名，則這整個簽章都是有效簽章。

程式實作

由於 hash 簽章系統都不會用到高級代數物件，在python即可進行實作

hashlib

import hashlib
import random

# 定義哈希函數 (SHA-256)
def hash_func(data):
    return hashlib.sha256(data.encode()).hexdigest()

# 將訊息轉換為二進位字串
def message_to_binary(message):
    return ''.join(format(ord(c), '08b') for c in message)


# 設定要簽章的訊息
message = "Hi! This is Cesare!"
binary_message = message_to_binary(message)
print(f"訊息的二進位表示: {binary_message}")
print(f"訊息的哈希值: {hash_func(message_to_binary('Hi! This is Cesare!'))}")

# Outputs:
# 010010000110100......10100100001
# 203790759a89f61......fffacc2

密鑰生成

# 生成私鑰的函數
seed = 42
def generate_private_keys(message_length,seed):
    sk0 = []
    sk1 = []
    for i in range(message_length):

        # 將 seed 值拼接到字串中，不同的 seed 會生成不同的私鑰
        sk0.append(hash_func(f"sk0_{i}_{seed}"))  # 拼接 seed
        sk1.append(hash_func(f"sk1_{i}_{seed}"))  # 拼接 seed
    return sk0, sk1

# 生成公鑰的函數
def generate_public_keys(sk0, sk1):
    pk0 = [hash_func(sk) for sk in sk0]
    pk1 = [hash_func(sk) for sk in sk1]
    return pk0, pk1

# 生成私鑰與公鑰
sk0, sk1 = generate_private_keys(len(binary_message),seed)

print("第一個位元的私鑰（有兩個喔）:")
print("sk0[0]: ",sk0[0])
print("sk1[0]: ",sk1[0]) 
pk0, pk1 = generate_public_keys(sk0, sk1)

print("\n第一個位元的公鑰（也有兩個喔）:")
print("pk0[0]: ",pk0[0])
print("pk1[0]: ",pk1[0]) 


# Outputs:
# 第一個位元的私鑰（有兩個喔）:
# sk0[0]:  5bcc70d9e8715729ca3ccc20c9a214b7b8dbafa7213ae60e9867a53dc88bf27a
# sk1[0]:  cfb13dfb3184d31f72233626ce444ef5fc177a5d09174bf23e66ccabc9f895e7

# 第一個位元的公鑰（也有兩個喔）:
# pk0[0]:  1d07a2da13e57d286afb4541f1cf01a46a27721c3ba8801c85c4127f18539984
# pk1[0]:  1c5aeabb30979ae915f27e6622a853e5169fd117cca131f95ba1f9531ec4bd0f

簽章

# 生成簽名的函數
def sign_message(message, sk0, sk1):
    signature = []
    for i, bit in enumerate(message):
        if bit == '0':
            signature.append(sk0[i])
        else:
            signature.append(sk1[i])
    return signature


# 簽章訊息
signature = sign_message(binary_message, sk0, sk1)
print("第一個位元的簽章:", signature[0])
print("第二個位元的簽章:", signature[1])

# Outputs:
# 第一個位元的簽章: 5bcc70d9e8715729ca3ccc20c9a214b7b8dbafa7213ae60e9867a53dc88bf27a
# 第二個位元的簽章: 7ae188d8eb4d2aded7b79fa5d8b9eb0349886fda0421fceb292e9f89936d56d3

驗章

# 驗證簽名的函數
def verify_signature(message, signature, pk0, pk1):
    for i, bit in enumerate(message):
        if bit == '0':
            if hash_func(signature[i]) != pk0[i]:
                return False
        else:
            if hash_func(signature[i]) != pk1[i]:
                return False
    return True
    
# 驗證簽章
valid = verify_signature(binary_message, signature, pk0, pk1)
if valid:
    print("簽章驗證成功！")
else:
    print("簽章驗證失敗！")


# Outputs:
# 簽章驗證成功！

缺點

相信你很快發現，我們這個系統是針對每個位元進行簽章，而每個簽章都要使用 256 位元的私鑰以及公鑰，可見最後整個簽章肯定很佔空間：

我們可以在剛剛的城市最後計算簽章大小

# 計算第一個簽章片段的大小
signature_0_size_bytes = len(signature[0]) // 2  # 簽章是十六進制表示，所以除以 2 來得到實際的 byte 數
print(f"signature[0] 的大小: {signature_0_size_bytes} bytes")

# 計算整個簽章的大小
total_signature_size_bytes = sum(len(sig_of_single_bit) // 2 for sig_of_single_bit in signature)  # 將所有簽章片段的大小加總
print(f"整個簽章的大小: {total_signature_size_bytes} bytes")

# Outputs:
# signature[0] 的大小: 32 bytes
# 整個簽章的大小: 4864 bytes

其實「簽章大小很大」這點是 Hash-based signature 常見的缺點。通過 NIST 後量子密碼競賽的另一個基於晶格密碼學的簽章系統，Falcon，就有比較短的簽章大小。舉例：Falcon 的最高安全參數 Falcon-1024 系統，簽出來的簽章大小只有 1500 byte 以下（ref: https://openquantumsafe.org/liboqs/algorithms/sig/falcon）

Takeaway

• Hash 函數 是現代密碼學中不可缺少的工具，擁有不可逆性和抗碰撞性，使其能夠有效地保護數位訊息的完整性。
• 量子計算的威脅：Grover's Algorithm 能夠降低 Hash 函數的安全性，因此我們需要考慮提高 Hash 函數的位元數，以確保未來量子時代的安全性。
• LD-OTS (一次性簽名方案) 利用 Hash 函數來保證每個位元的安全性，但其簽章大小較大，這是使用 Hash-based signature 系統的常見問題。