取後放回之平均數

有一組資料 A 包含五個不同的數字 {2, 3, 5, 7, 13}，其中每個數字被抽取的的機率相等。設每次抽到的數字為隨機變數 X，則其分配函數 PMF 為

抽樣分配

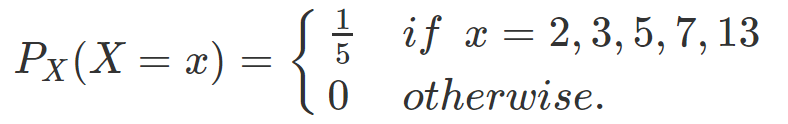
若從資料 A = {2, 3, 5, 7, 13} 中一次取出一個數字，紀錄其值後放回（取後放回），重複此過程 4 次得到 X1, X2, X3 ,X4，並計算取出的均數

中央極限定理

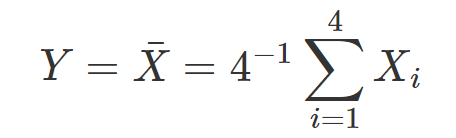
根據中央極限定理 （CLT） ，

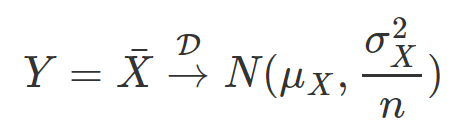
即當樣本數足夠大時，樣本平均數會漸進收斂到 Normal 分配。計算此處參數值

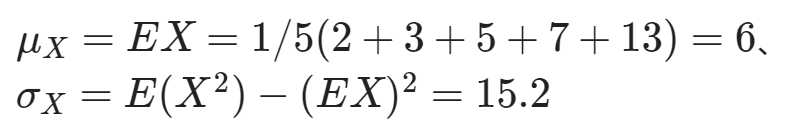
其中分別為隨機變數 X 的母體均數與母體變異數。所以當樣本足夠大時，依據 CLT， Y 將漸進收斂到 N(6, 15.2/4) = N(6, 3.8)。

下圖為模擬 N = 1,000,000 次的的值的直方圖，實驗結果顯示樣本均數大致呈現對稱分布。

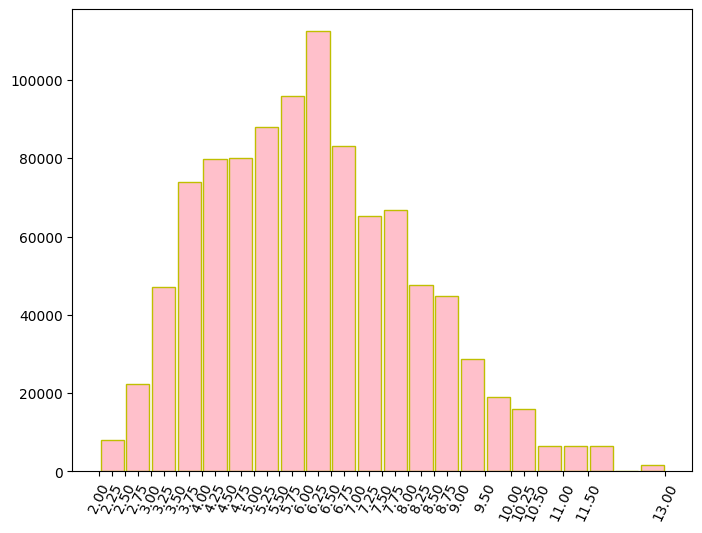
Python 程式碼如下。注意！此處只能使用直方圖，而不能使用長條圖。畫直方圖時 ，可選擇開啟 plt.hist(..., densiyt=True) 功能。若開啟該功能，則 Y 軸為數量；若不開啟，則為小於 1 的密度比率。而此圖縱軸為數量。

import matplotlib.pyplot as plt
from scipy.stats import norm
import numpy as np
import random

# Compute mean and variance of random variable X.

mu = np.mean([2, 3, 5, 7, 13])
var = np.var([2, 3, 5, 7, 13], ddof=0)
print('mu = {}, var = {}'.format(mu, var))


# Withdraw with Replacement

N = 10**6 # 抽樣次數
n = 4 # 樣本數

X = np.array([2, 3, 5, 7, 13])

W = np.random.choice(X, size=(N, n), replace=True) 
Y = np.mean(W, axis=1) # Y = {\bar X}
print(f'樣本均數有: {np.unique(Y)}')

plt.figure(figsize=[8, 6])
plt.hist(Y, bins=22, color='pink', edgecolor='y', rwidth=0.9,
         align='mid', label='Sampling Scatter')

x = np.linspace(np.min(Y)-1, np.max(Y)+1, 1000)
y = norm.pdf(x, loc=mu, scale=np.sqrt(var / n))

plt.xticks(np.unique(Y), rotation=65)
plt.show()

再來加入常態分配之 PDF，並將圖片的縱軸從數量改為密度比率。如下圖，可看出模擬 1,000,000 次之下，樣本均數的分布已經與常態非常接近了。

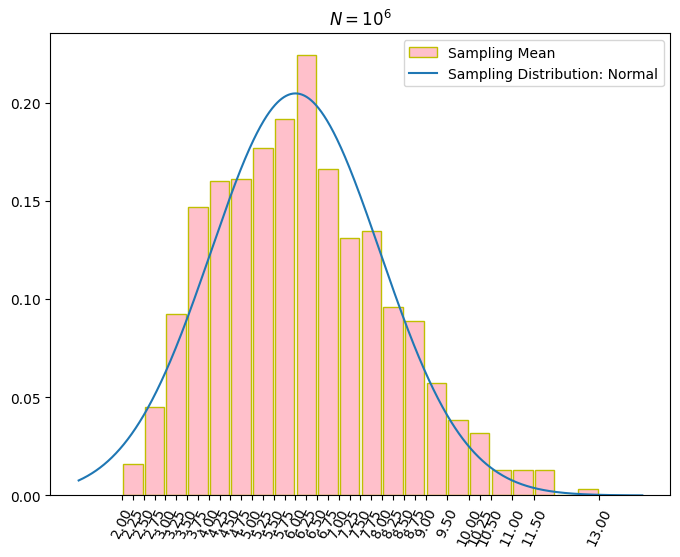
程式加入常態分配且縱軸改為密度比率的 PDF 後的程式碼如下。

# Sampling Distribution of sample mean 
# CLT

N = 10**6 # 抽樣次數
n = 4 # 樣本數

x = np.array([2, 3, 5, 7, 13])

W = np.random.choice(x, size=(N, n), replace=True) 
Y = np.mean(W, axis=1) # Y = {\bar X}


plt.figure(figsize=[8, 6])
plt.hist(Y, bins=22, color='pink', edgecolor='y', rwidth=0.9,
         align='mid', label='Sample Mean', density=True,
         histtype='barstacked')

# By CLT, Y ~ Normal(mu, sigma^2 / n)
x = np.linspace(np.min(Y)-1, np.max(Y)+1, 1000)
y = norm.pdf(x, loc=mu, scale=np.sqrt(var / n))

plt.plot(x, y, label='Sampling Distribution: Normal')

plt.xticks(np.unique(Y), rotation=65)
plt.title(r'$N = 10^{:.0f}$'.format(np.log10(N)))
plt.legend()
plt.show()

足夠大的樣本數？

比較不同的模擬（抽樣）次數下，樣本均數與常態分配的關係。如下圖，隨模擬次數的增加，樣本均數越貼近常態分配，驗證了 CLT 理論。

另外，有一說法說明多大的樣本數（在此案指模擬/抽樣次數）會使 CLT 成立：「當樣本數大於 30 或 50 時，通常 CLT 會成立。」但是，如下圖，模擬 50 次也沒有接近常態分配，尤其是在左尾與右尾部分（但也可能是因所設方格寬度太小的關係導致不像常態）。

以實務上來說，大樣本數建議依據每次所遇到的母體分布樣態而定，不能一概而論。如果母體的分配原就與常態非常不相像，例如：左、右偏嚴重，那就需要非常多的樣本數才會漸進常態分配。而到底有多少的樣本才可以說會漸進常態分配呢？可因個案，依靠模擬、抽樣等方式實驗得出結論。除已經有人提出一些判斷法則之外，例如：二項分配，筆者認為誰也說不準。

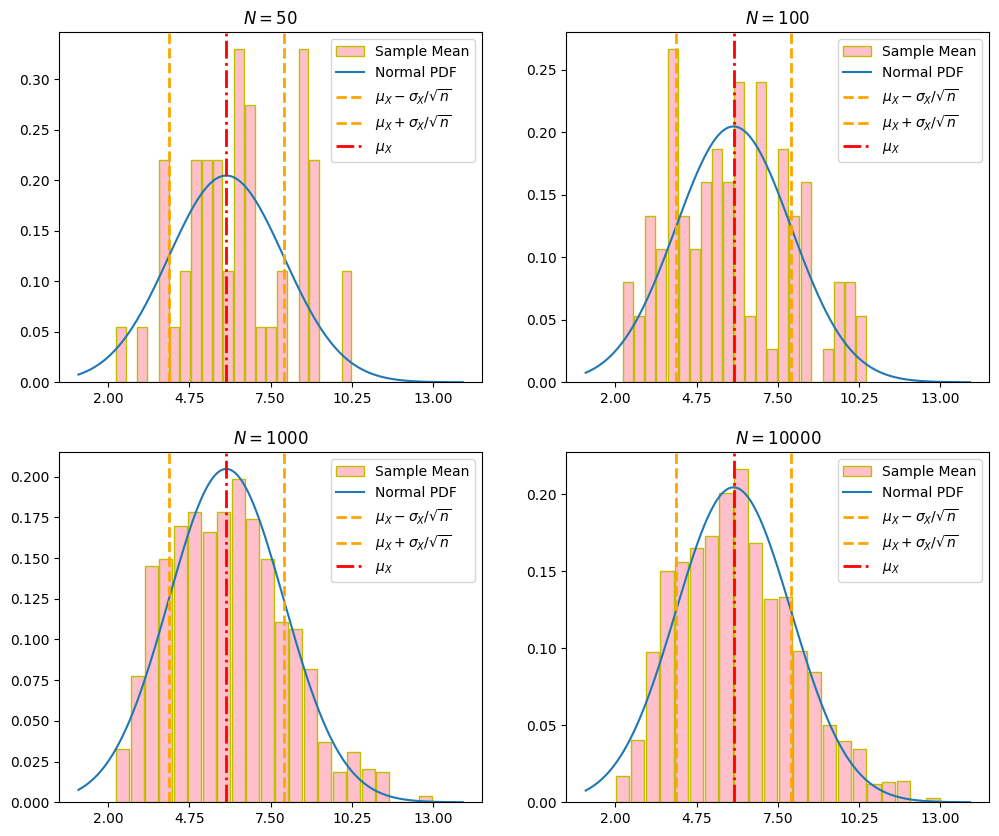
程式如下，其中若需要旋轉橫軸刻度可使用 ax[k][l].tick_params(axis='x', labelrotation = 65)。

# How many sample sizes does CLT need ?

N = [50, 10**2, 10**3, 10**4] # 抽樣次數
n = 4 # 樣本數
X = np.array([2, 3, 5, 7, 13])

fig, ax = plt.subplots(2, 2, figsize=(12, 10))

k = 0
l = 0

for i, j in enumerate(N):
  k = 0 if i<2 else 1
  l = 0 if i%2 == 0 else 1 
  print(k, l)

  W = np.random.choice(X, size=(N[i], n), replace=True) 
  Y = np.mean(W, axis=1) # Y = {\bar X}

  ax[k][l].hist(Y, bins=22, color='pink', edgecolor='y', rwidth=0.9,
          align='mid', label='Sample Mean', density=True,
          histtype='barstacked')
  
  # By CLT, Y -> Normal(mu, sigma^2 / n) in distribution
  x = np.linspace(np.min(X)-1, np.max(X)+1, 1000)
  y = norm.pdf(x, loc=mu, scale=np.sqrt(var / n))


  ax[k][l].plot(x, y, label='Normal PDF')
  
  ax[k][l].set_xticks(np.linspace(min(X), max(X), 5)) #, rotation=65

  # Rotating X-axis labels
  # ax[k][l].tick_params(axis='x', labelrotation = 65)
  
  ax[k][l].axvline(x=mu - np.sqrt(var / n), color='orange', linestyle='--',\
                   label=r'$\mu_X - \sigma_X/\sqrt{n}$', lw=2)
  ax[k][l].axvline(x=mu + np.sqrt(var / n), color='orange', linestyle='--',\
                   label=r'$\mu_X + \sigma_X/\sqrt{n}$', lw=2)
  ax[k][l].axvline(x=mu, color='r', linestyle='-.', label=r'$\mu_X$', lw=2)
  ax[k][l].set_title(r'$N = {}$'.format(N[i]))
  ax[k][l].legend()

plt.show()

小結

本文以對一組有不同數字的資料 {2, 3, 5, 7, 13} 取後放回抽樣 4 個數字取平均，介紹該均數的抽樣分配及大樣本下才會成立的中央極限定理，並接著說明母體分配情形對抽樣後的樣本均數是否得以相對較小的樣本數漸近常態分配影響重大。所謂使中央極限定理成立的大樣本，並非盲目地以樣本數是否大於 30 或 50 界定之，能否夠套用中央極限定理還需要更嚴謹的事前實驗，有充分證據顯示定理成立才可安心使用。