為什麼需要多項式承諾?

多項式承諾方案能夠讓承諾者發送一個基於多項式的承諾方案，例如:P(x)。
透過計算承諾得出一個多項式.計算過程其實和一般的承諾方案一樣，在一般的方案之下，承諾者可以公開原本的公式，目的是給驗證者可以檢查承諾方案是不是對應於所屬的公式。在多項式承諾方案中，有一個額外的屬性可以讓承諾者可以對自己所用到承諾多項式的進行特定的評估，而在評估過程中是不用透露多項式的公式。例如，承諾者基於P(x)=K產出一個證明，承諾者可以將這證明發給驗證者，而驗證者可以只利用這個承諾來驗證證明。
注意: 多項式承諾方案是具有兩大類別，第一類是不需要涉及私隱計算，第二類是需要涉及私隱計算(所以會有一個額外屬性)。

多項式承諾方案在零知識證明的應用中具有非常大的價值。
證明者可以透過多項式承諾方案來證明自己是知道一些滿足產出證明的多項式的條件，而且又不用向驗證者透露多項式的資訊。所以在整過驗證過程中，是沒有其他人會知道當中的多項式是什麼。

另外，會用到多項式方案的原因是利用承諾可以進一步地減少它的大小，而大小會比傳統的多項式小得多，
換個角度來說，可以把當作是對多項式進行壓縮，變成一個承諾證明。而壓縮的程度就需要取決於方案的能力，
不同方案會具有不同的特性和壓縮程度。例如，在KZG多項式承諾方案中，任意大次數的多項式可以被壓縮為由單一群體元素組成的承諾。

因為PLONK需要一個非交互式的證明，而證明需要具有以下特性:

1. 具常數的大小
   假設PLONK的見證是u:
   
   而u可以被編碼成一個多項式
   
   這個多項式可以用於多項式承諾方案(PCS)以產生一個具單值的承諾。

2. Non-Revealing:
   PCS 可以允許驗證者在不知道u的內容的情況下去查詢及驗證附加資訊和其相關的所有資料，
   而其他承諾方案(如Pedersen承諾、Merkle樹等)都是要求證明者透露一部分或全部與承諾有關的資料。

3. 具同態:
   PCS 驗證者可以在無需訪問的情況之下執行多項式算術化及提交相關的多項式。

4. 可執行批次處理(BPCS):
   PLONK 需要證明者提交多個多項式，當中部分或全部多項式需要在不同的輸入下進行驗證，要同步在不同地方輸入，就可以使用 BPCS 來實現。這樣做的話，可以降低證明者和驗證者的運算時間成本。

多項式餘數定理

假設f(X)是一個多項式= kX^2 + bX + c ，而a 是X的其中一個點，所以當X = a 時會得出f(a)的值，因此當f(X) - f(a)，會有一個數值為a的根。
如下圖所示: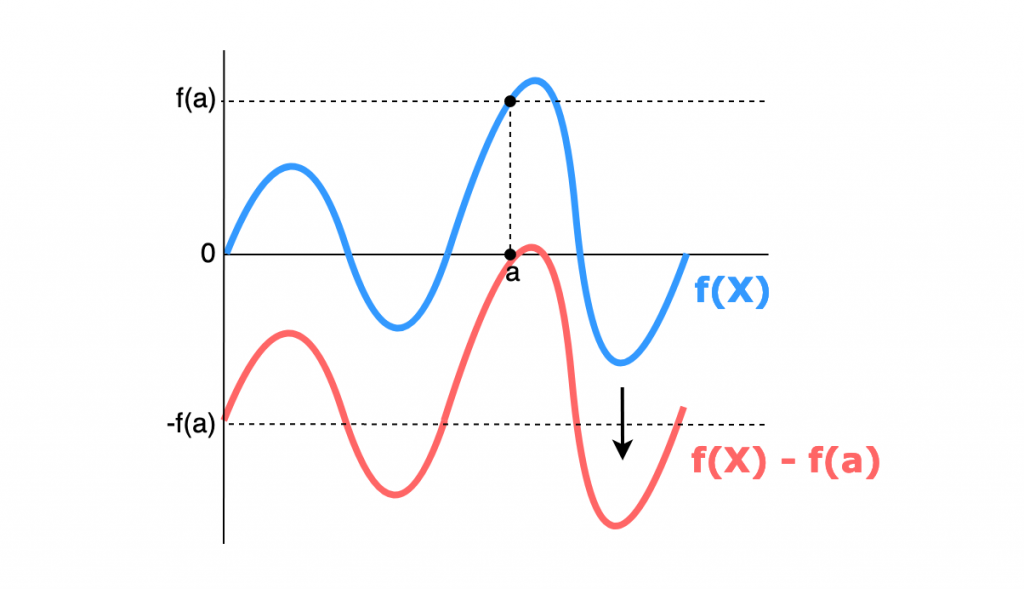

然而，當f(X) - f(a)會有一個為a值的根，所以進行線性的因式分解時，會包含一個(X-a)的多項式。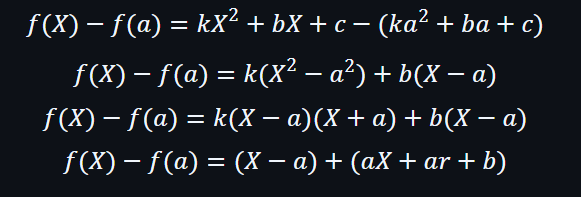

相信大家看到多項式的餘數定理，可以留意到當驗證者進行驗證時，其實可以很輕鬆完成到這動作。
如果等式成立，就表示 (X - a) 為 f(X) - f(a) 的因數。
對於a點的選擇，在非交互式的前提下，在可信任設置上會得到。

多項式承諾的應用

多項式承諾應用方向總結起來可以分為三大類

1. 數據可用性
   Celestia 通過欺詐證明實現，ETH 在通過protoDanksharding後的版本和 Polygon Avail 則採用了 KZG 多項式承諾方案。
   要實現數據可用性的價值就需要有以下三點:
   A. 區塊資料透過糾刪碼增加資料的可靠性，例如區塊鏈節點只需要透過任意的50%資料就可以還原出原本100%的資料，
   B. 輕節點能夠合力採樣及儲存足夠多的片段資料，通過互相合作，各負責不同部分的資料，保證最終能還原100%的完整資料，
   C. 最後一個就是需要正常的p2p網路讓各節點們可以隨時分享片段資料，以保證數據的流通性及組合性能。

2. 數據結構優化
   Verkle Tree 的概念是源於2018年，被視為ETH升級的其中一個重要部分。跟Merkle Tree相比之下，在證明的大小上，
   Verkle Tree 是有一個明顯的提升。例如在一個規模在十億級別的數據情況中，Merkle Tree 的證明大約需要 1kB，而在Verkle Tree 就會小於 150Bytes。
   Merkle Tree 和 Verkle Tree 都是同樣能實現 Proof of Inclusion（PoI），但Verkle Tree 只是需要 KZG root 和相關數據就能進行驗證，過程中不需要其他的證明，因為可以減少了數據的流量。

3. 零知識證明應用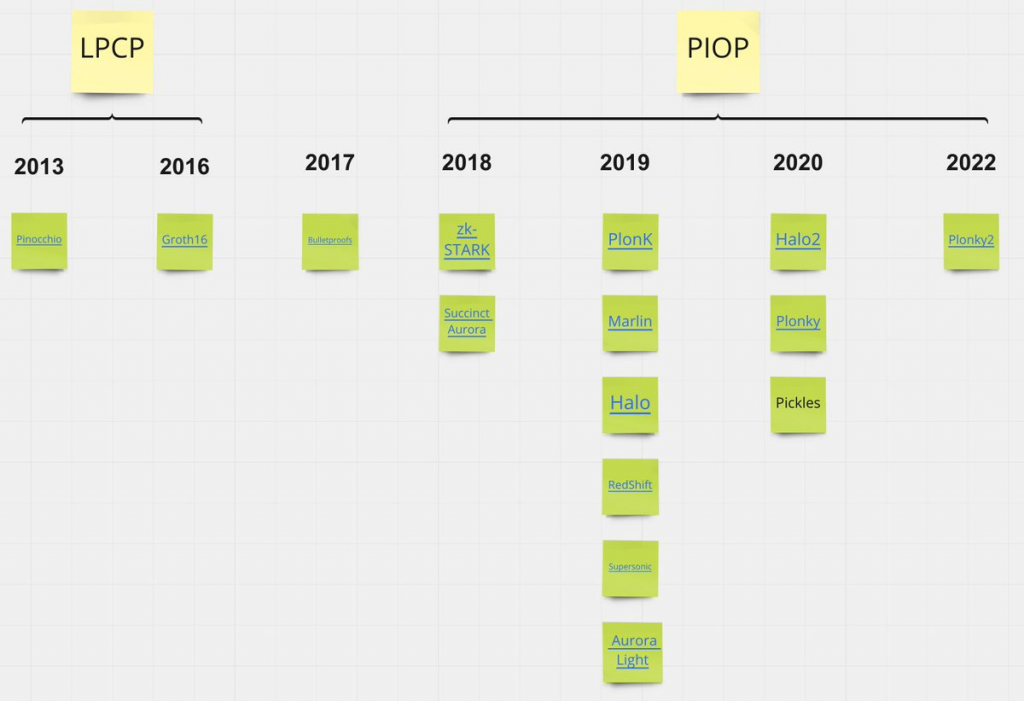
   

Zksync，Zkswap，Scroll等都是給零知識證明提提供多項式承諾方案，可以大大提升區塊鏈的延伸能力，從而使到有更多場景可以利用到零知識證明技術來解決當下的痛點，及創造新的機會。早期零知識證明技術屬於線性 PCP 類。除了要求可信設置，其缺點就是如果需要為不同的算法方案提供證明，都需要重新進行一次新的可信設置。 而創新的 PIOP 類就可以支持到通用設置包括不需要信任的設置。對於新的零知識證明算法可以視為 PIOP（Polynomial Interactive Oracle Proof，多項式交互預言證明）+ PCS（Polynomial Commitment Scheme，多項式承諾方案）。前者可被視為是證明者用來說服驗證者的約定程序，而後者使用數學方法確保該程序不會遭到破壞，兩者可以因應情況而自己搭配。

參考資料:

1. Polynomial Commitment Schemes
   https://docs.scroll.io/en/learn/zero-knowledge/polynomial-commitment-schemes/

2. Data Availability Sampling（一）：為什麼會需要 DAS？
   https://medium.com/taipei-ethereum-meetup/data-availability-sampling-part-one-why-das-dc17f83355b5