在上一篇簡單地講解了多項式承諾的價值及應用，在眾多的多項式承諾中，KZG是其中一個受歡迎的多項式承諾，也是PLONK的其中一個常用的多項式承諾。
KZG 多項式承諾（KZG Polynomial Commitment）也被稱為卡特多項式承諾方案，是 Kate，Zaverucha 和 Goldberg 三人一起發表的。
在一個多項式方案中，證明者需要計算一個多項式承諾，然後可以在多項式中任意一點進行驗證，也就是說必須具有可被驗證的能力，
而那多項式承諾方案能證明多項式在某一特定位置的值與正確的值是相同的。

重溫一下什麼是承諾，當一個承諾值(在數學上，是指橢圓曲線上的一個點)由證明者發送出去給驗證者時，證明者不能再改變產出承諾的多項式。因為在過程中只能夠對一個多項式提供有效的證明，如果產出承諾的多項式改變了，就不能再產出相同的承諾值。

橢圓曲線

橢圓曲線的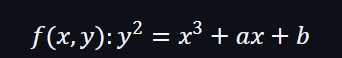公式例子:

加上a,b的真實數值後，f(x,y)的參考圖像如下，圖像的模式是基於a,b的值。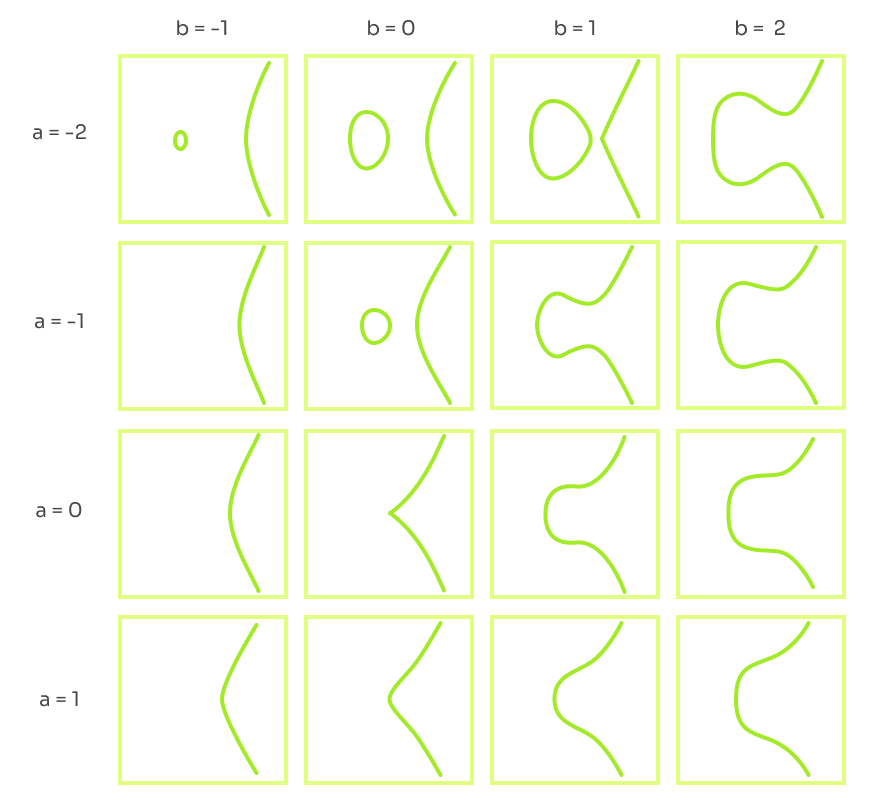

橢圓曲線的點都是在x、y軸上的，及在有限域(Fp)上，而有限域中的p是一個質數，換言之，x、y軸上的點都是在同一個集合[0,1,2,3,...,p-1]，範圍由0到p-1。而且對Fp內的任何2個元素，可以在模數p下進行加法和乘法。
而在有限域上使用橢圓曲線的原因是對於計算機來說，執行整數的算術運算會比執行實數的算術運算更容易。
為了讓大家更好理解，會加入例子說明:
假設 a = -1, b = 0, 有限域是F61。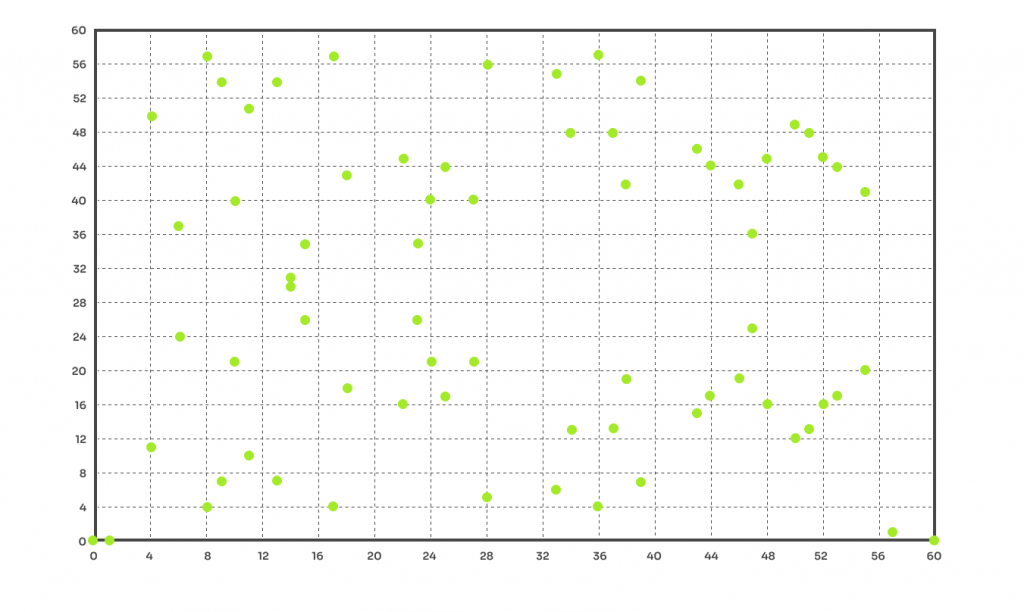

從上圖所示，
橢圓曲線上的任兩點都可以透過特定的方式進行相加和相減。對於這種結構，具有某些良好的特性。例如，添加或減去曲線上的任兩點都會導致同一橢圓曲線上的另一個點。這些屬性可以透過數學物件組來概括。需要在某個集合上定義一個標準組G和一組操作O。
因此，我們可以說有限域上橢圓曲線的點集合是透過加法運算形成一個群。例如，整數的集合 也形成一個組。好處是群是已經通過深入研究的數學對象。透過證明橢圓曲線形成一個群，我們可以使用任何關於群的陳述，然後將其應用於橢圓曲線。

一個團體需要有一個中性的元素e和每個元素需要分配一個相反的元素。而每個群都可以執行一組O操作及能用在G內的任何一個元素和配合一個中性元素e，最後得出一個結果x。對於相反的元素，都可以執行相同的操作。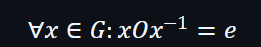

換成乘冪例子也是同樣沒問題的，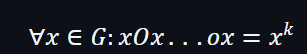

在橢圓曲線的應用例子中，比較常用的操作符號有加號和乘號。

離散對數問題

在橢圓曲線上，離散對數會帶來一些難題，因為離散對數問題（DLP）被認為在橢圓曲線上是很難解決。
假設: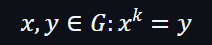

然而這是很難找到k值，當G的大小愈大，所面對的難度就愈大。這就正如設置戶口的密碼，當密碼的長度愈長，就愈難被破解。
當根據x來計算y時，我們是不知道任何有效率的演算法來計算k值。在密碼學中的標準假設，許多現代協議都是基於 DLP 的困難度。為什麼會是指困難度? 因為DLP是能被解決，只是一般都是很難在一個合理或短的時間內有完成計算得出結果。如果將協議的困難度建基於DLP的困難度，換言之只要沒有人能夠在橢圓曲線上有效率地計算 DLP，協議就很難被破解。

橢圓曲線運算

在 KZG 中，會將多項式評估進行編碼成為橢圓曲線組中的元素。
如果我們進行對f(a)的評估，可以將它們編碼為群元素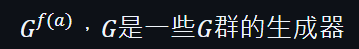

在這情況下，橢圓曲線將非常有用，因為透過DLP可以對f(a)評估及加密為G。
不過，特別之處在於可以取得秘密值 (a, b, ...) 然後編碼為橢圓曲線點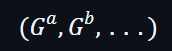

而且依照能夠執行一些操作而不用透露其秘密值(a，b，...)。
在零知識協議下，證明者能發送編碼為橢圓曲線點的多項式評估給驗證者，而驗證者可以在不知道實際值的情況下執行算術運算來進行驗證。
針對這例子的各種運算情況(加、減、乘、多項式)，可以列出以下表格: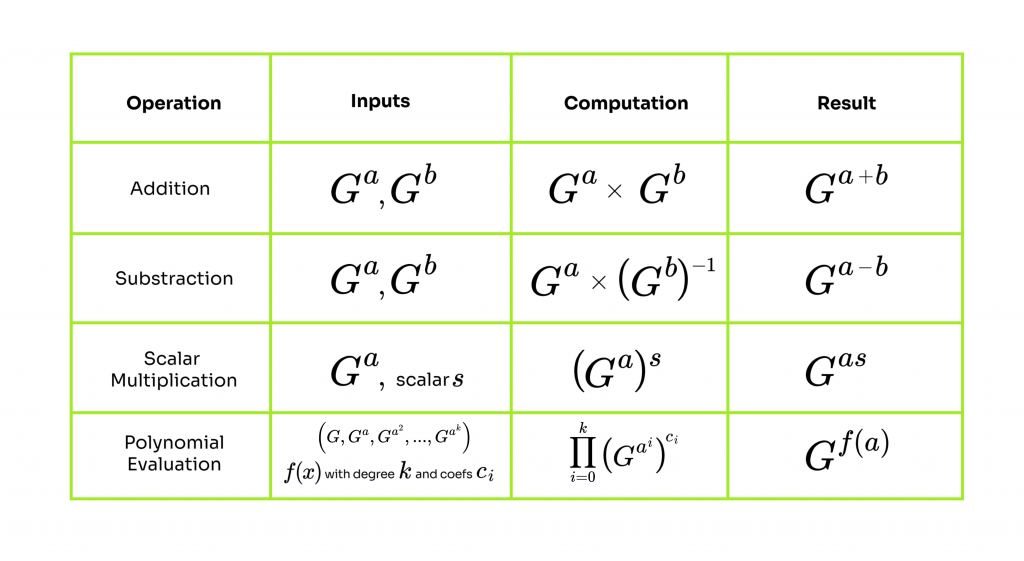

在第一行是標準的群運算。
在第二行是先取得數值的逆運算對象，再執行群運算。
在第三行是標量乘法運算，即是求取乘冪。
在第四行是多項式評估，假設存在一個多項式f(x)具有degree k如下: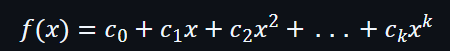

在某個a點，對於f(x)的評估可以以下面公式表達: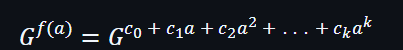

然後可以再進一步轉換成以下公式: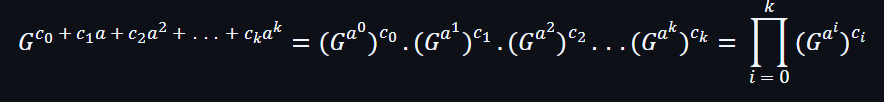

曲線配對 (Curve Pairings)

本質上是曲線配對e，只需要得到兩個點，分別是p點和q點: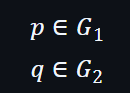

然後將它們在某一目標群中進行配對，如下圖所示: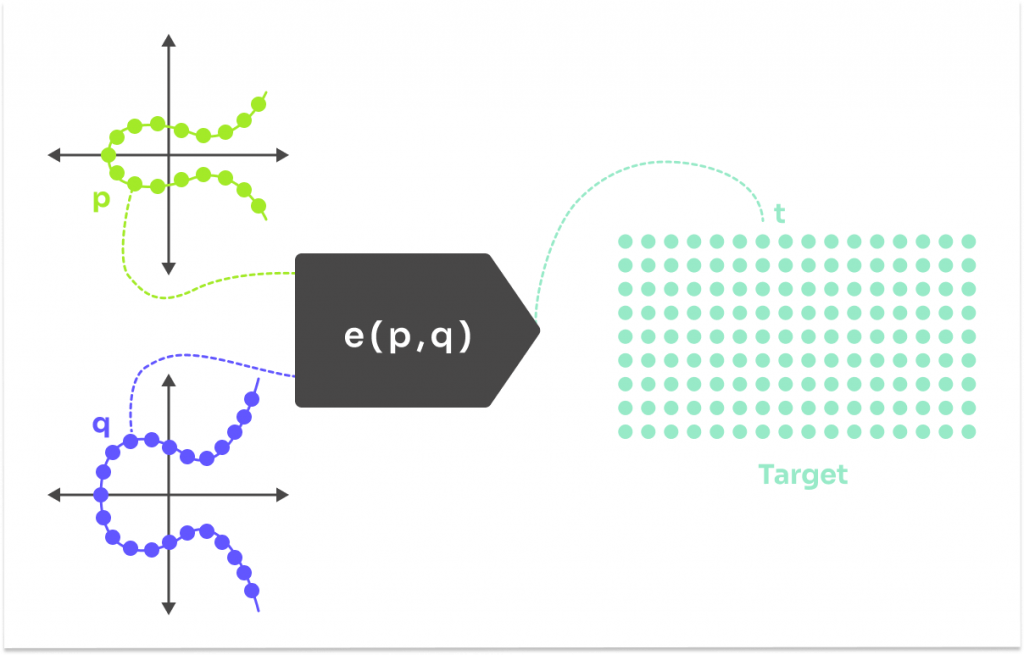

將把配對的動作視為一個黑盒，只要知道它們具有以下屬性就足夠了: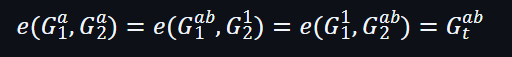

多琪式比較 (Comparing Polynomials)

對於多項式的比較，可以讓兩個多項式在同一點進行比較。雖然方法簡單，不過對於有足夠大的域的多項式，所得出的效果是很好。
假設該點是x，如果兩個多項式在x點是有相等的值，則: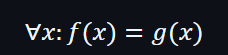

但是此檢查也可能會接受不同但在隨機選取點有交集的多項式。
為了計算出失敗機率，就要知道兩個不同多項式的交集上限是多少。

假設有兩個多項式，分別是p(x)及q(x):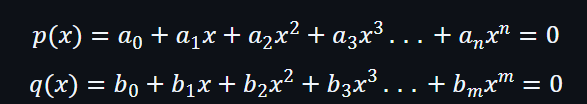

存在一個上限 d 小於或等於 S，n和m也不會大於d的。
為了找到交集的點，需要解決以下方程式: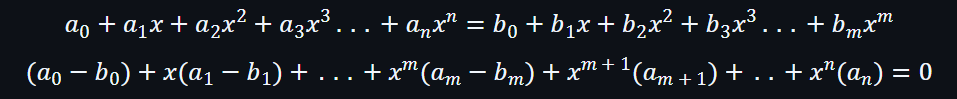

因此，可以看到 n 小於或等於 d，而n不能多於n個根，所以f(x)和g(x)的最多交集點是n個點，上限是d。
所以失敗機率的計算公式為:

可以留意到當域愈大，失敗機率就愈小。
通過以上方式，只需透過一次評估就可以有效地比較兩個多項式。

參考資料:

1. KZG polynomial commitments
   https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html