KZG 的好處是有一個承諾和開放狀態,而且由一組不變數量的元素組成,不過缺點就是 KZG 有可信設置。
可信任設置表示其他人(自己除外)是不能知道用於產生公共參數的私鑰是什麼。
現在用一個例子說明,假設存在有一個可信任設置,對於一個不公開的資料s群,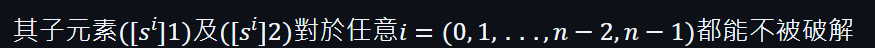
在實際應用的例子中,可信任設置會使用安全多方計算(MPC)的方式,透過利用一組計算機一起來創建s群元素,而沒有任一部計算機可以知道s的值,所以在這情況下只有奪得或控制所有計算機才能知道s。
公開參數SRS是由生成器產出的,對於任何想要產出一個多項式做出承諾的人來說,SRS 是必要的。
SRS其實是一個點的集合:
當中的T是在有限域Fp內,Fp會利用於隨機私鑰來生成SRS。
有一個重要的事,就是證明者一定不能知道T,因為會讓證明者能夠偽造一個假的證明,同時也僧令到協議失效。
所以需要養成一個習慣,就是在完成生成器的過程後,執行刪除T的動作。但值得注意的是,有關T的一些信息
是公開的,因為它是在 SRS 內。不過T值被編碼為橢圓曲線上的點,基於橢圓曲線上的離散對數問題,要是想由橢圓曲線上獲取到T值是很難的。
而 SRS 可以重複使用來保障"證明"能滿足degree d的上限條件的任意多項式的評估 d。
因此可以理解為 KZG 具有一次性可信任設置。
整個方案會根據以下簡單的事實。對於任意變數的多項式 f(x) 的 degree d,
存在一個 f(z)=v 相當於檢查多項式是否存在 w(x) 的 degree 小於 d: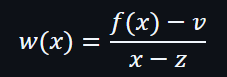
由於我們有一個多項式f(x),也知道f(z) = v。
因此可以利用f(x)來組成 f1(x) = f(x) - v ,當x=x時,會出現 f1(z) = f(z) - v = 0。
所以可以知道z是f1(x)的根,可以轉換成以下公式: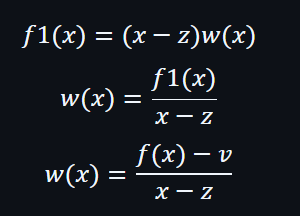
根據觀察結果,可以留意到透過以上例子是可以將評估檢查轉換為可除性檢查,由可除性檢查轉換為評估檢查也是可以的。
僅通過在單個隨機選擇的點進行評估就可以在一個高信任度的情況下進行驗證表達式的相等性。
接下來,就是講解KZG的流程
數值T在有限域Fp可以被隨機選擇及SRS由乘冪群產生器G1, G2所生成的。另外,證明者是不知道T值,所以設置步驟不能被證明者完成。
證明者會有秘密的多項式f(x)而degree的上限為d,為了提交f(x),證明者需要發出一個承諾C: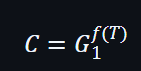
這表示承諾是一個群的元素,它只是一條曲線上的其中一個點。1
大家可能會覺得好奇怪,為什麼要求證明者對f(T)計算評估,即使表示在計算上證明者是無法訪問T,
所以他們又是怎樣計算評估? 因為SRS的存在,所以證明者可以做到相關計算評估。
假設存在一個f(x)如下: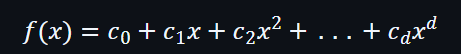
在乘冪群產生器中可以被計算為: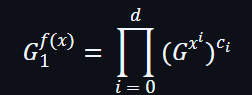
在這裡,大家都可以知道怎樣計算到承諾G: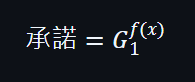
將T代入x就如下: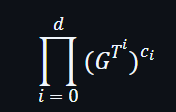
由於SRS已包含所有G在T位置的元素,所以證明者是不用知道T值來計算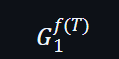
因此,證明者只需要計有算到f(x)在T上的值就可以給驗證者做驗證。
換言之,只要通過證明者和驗證者雙方都認可的公式及環境下進行計算都是可靠而且能保障到大家的私隱。
證明者需要在位於V = f(z) 的點上打開多項式f(x),所以需要計算一個證明(witness)。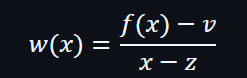
過程中,證明者需要完成多項式的計算,目的是證明存在一個證明可以驗證到f(z) = v 。
所以多項式w(x)會是一個對f(z) = v 的證明。與"Commit"過程一樣,在不需要知道T值的情況下,計算: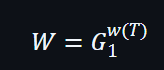
最後證明者會產出一個組合(v, W)
在這部分是多項式承諾方案進行評估多項式正確的地方。如果驗證動作成功,就表示驗證者是相信多項式在z點上的評估。
因為也證明存一個: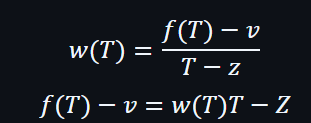
證明者是不知道T值,但證明者是可以發送f(T)的值。另外,w(T)是橢圓曲線上的一個點: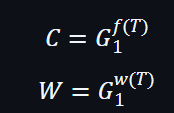
所以進行檢查時﹐可以轉換為以下公式: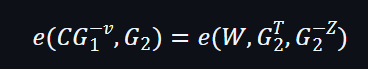
驗證者只需要知道 (C, z, v, W)及公共參數SRS就可以進行驗證。
從上面的公式,大家可以看到左邊有一個C,這個C就是承諾,由證明者發出的。同時,證明者需要提供一個v及基於v來計算G1,而G2是SRS的一部分。
在公式的右邊部分,驗證者會獲得到一個W證明及來自SRS的G2。同時,驗證者是有一個z值及基於z來計算G2。另外,有一點要留意是驗證者在沒有進行配對下是不能夠計算到: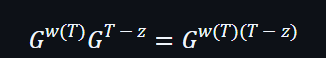
但在具有配對屬性的情況下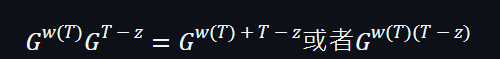
一個完整的流程如下圖所示: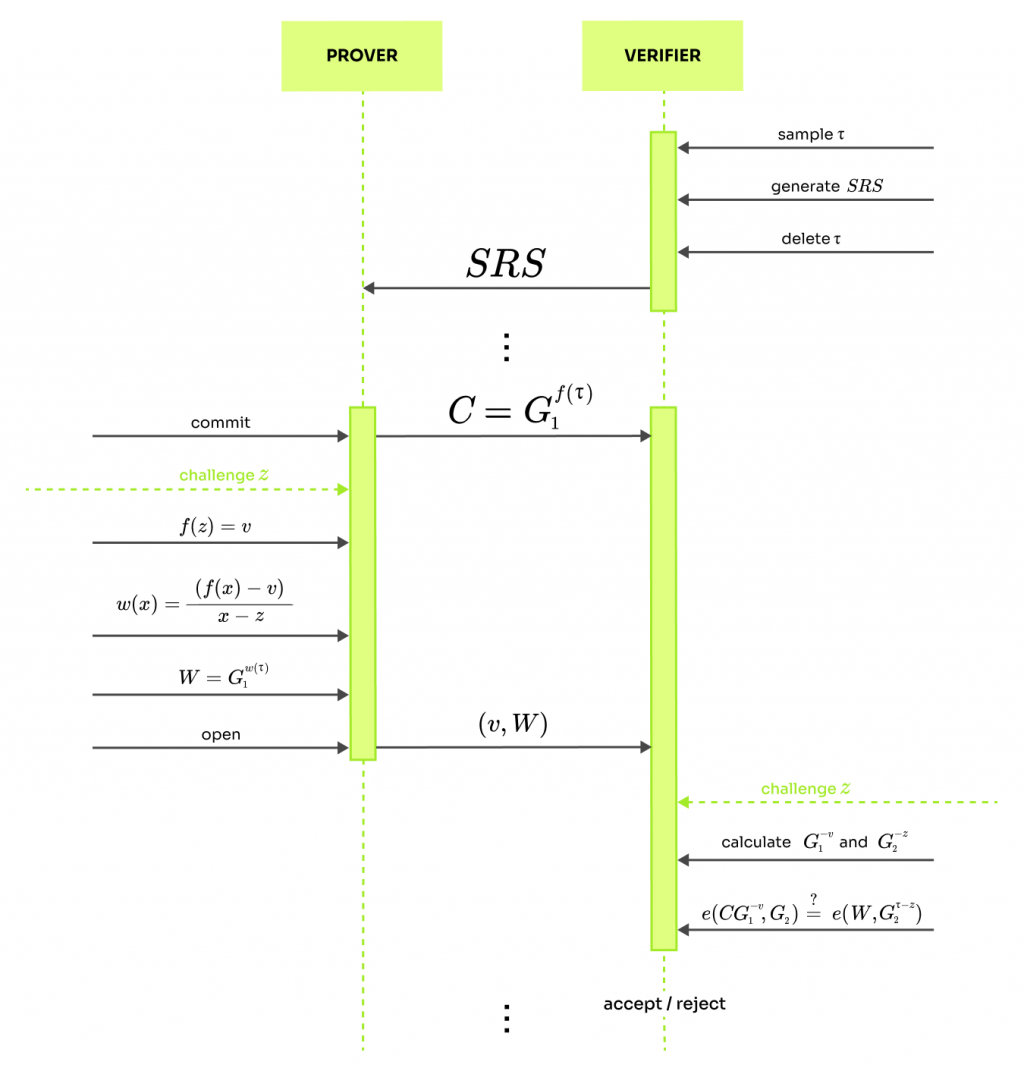
參考資料:
Understanding Zero-Knowledge Proofs: Part 4— Polynomial Commitments
https://medium.com/@bhaskark2/understanding-zero-knowledge-proofs-part-4-polynomial-commitments-e6e2a6a5e5e8
The KZG/Kate Polynomial Commitment Scheme
https://risencrypto.github.io/Kate/
什麼是 KZG 多項式承諾
https://web3caff.com/zh_tc/archives/39013
Constant-Size Commitments to Polynomials and Their Applications
https://www.iacr.org/archive/asiacrypt2010/6477178/6477178.pdf
