今天是學習Python的倒數第3天，我要實作的是圓周率的蒙地卡羅模擬法，它是一種基於機率與統計理論的計算方法，常用於預測具有不確定性事件的可能結果。

什麼是圓周率的蒙地卡羅模擬法?

圓周率的蒙地卡羅模擬法是一種利用隨機數與統計學來估算數學常數 𝜋 的方法。這個方法透過在一個已知面積的形狀（通常是正方形）內隨機生成大量點，來計算落在另一個形狀（例如圓形）中的點的比例，從而估算出圓周率的值。

步驟：

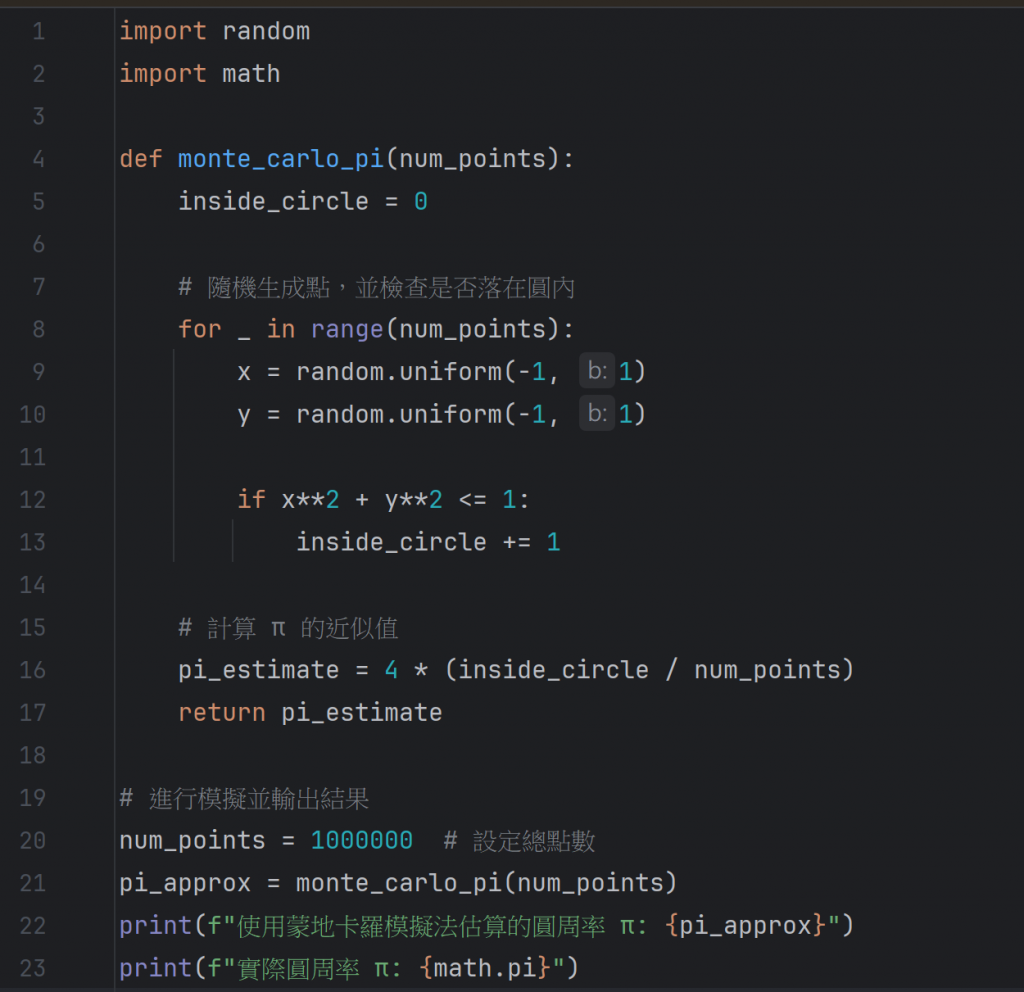
1.生成隨機點： 使用 random.uniform() 生成一組隨機點 (x, y)，這些點會被限制在邊長為 1 的正方形內。這是為了模擬投擲點落在一個圓與正方形中的情況。

2.計算點是否在圓內： 這些隨機生成的點有些會落在內切於正方形的圓中。根據圓的方程式，若
𝑥^2 + 𝑦^2 ≤ 1，則表示該點位於圓內。

3.計算圓內點的比例： 會生成大量的點，並計算落在圓內的點與總點數的比例。理論上，這個比例應該接近於圓面積與正方形面積的比值，也就是 𝜋/4。

4.估計圓周率： 透過點的比例，我們可以估算出 π 的值，公式為：
𝜋 ≈ 4 × (圓內的點數/總點數)

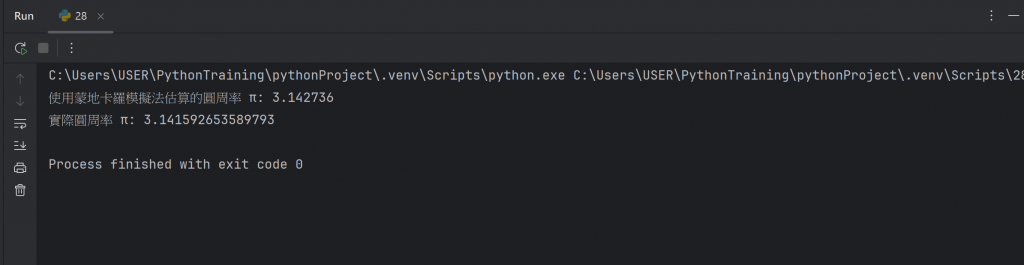
5.顯示結果： 最後，會輸出結果以及估算的 π 值，並可以透過不同的點數來觀察結果的變化。

程式碼:

輸出結果: