大家好～這裡鐵匠史密斯
實在抱歉，這周末的三篇文章會在後面重新整理~
而且，目前來說，找不出天花板、地板渲染的原理，公式以及其相關文獻日後會再找出，明日再嘗試以我的觀點來解釋渲染的原理
今日嘗試整理了手算的規律後找到天花板、地板隨著距離 fDistanceToWall的規律

藉由迭代找出規律

昨日定義了 nCeiling 以及 nFloor， 代表了
**天花板的最低界線 = 牆壁最高點 **
**地板的最高界線 = 牆壁最低點 **
兩者以 screen 畫面的垂直中心為基準開始分配天花板、地板的比例: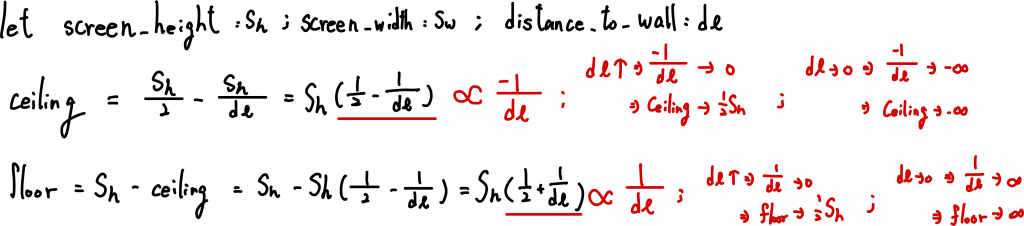

// Decide the height of the wall by distance to the wall
int nCeiling = (float)(nScreenHeight / 2.0) - nScreenHeight /((float)fDistanceToWall);
int nFloor   = (float)(nScreenHeight / 2.0) + nScreenHeight /((float)fDistanceToWall); 
// nFloor = nScreenHeight - nCeiling;

由於我們光可以走的最大距離 = map 的最大長度 = 16 個單位
所以，假設以 fDistanceToWall = 16 進行遞減，直到 fDistanceToWall = 1
來查看渲染畫面中該欄的結果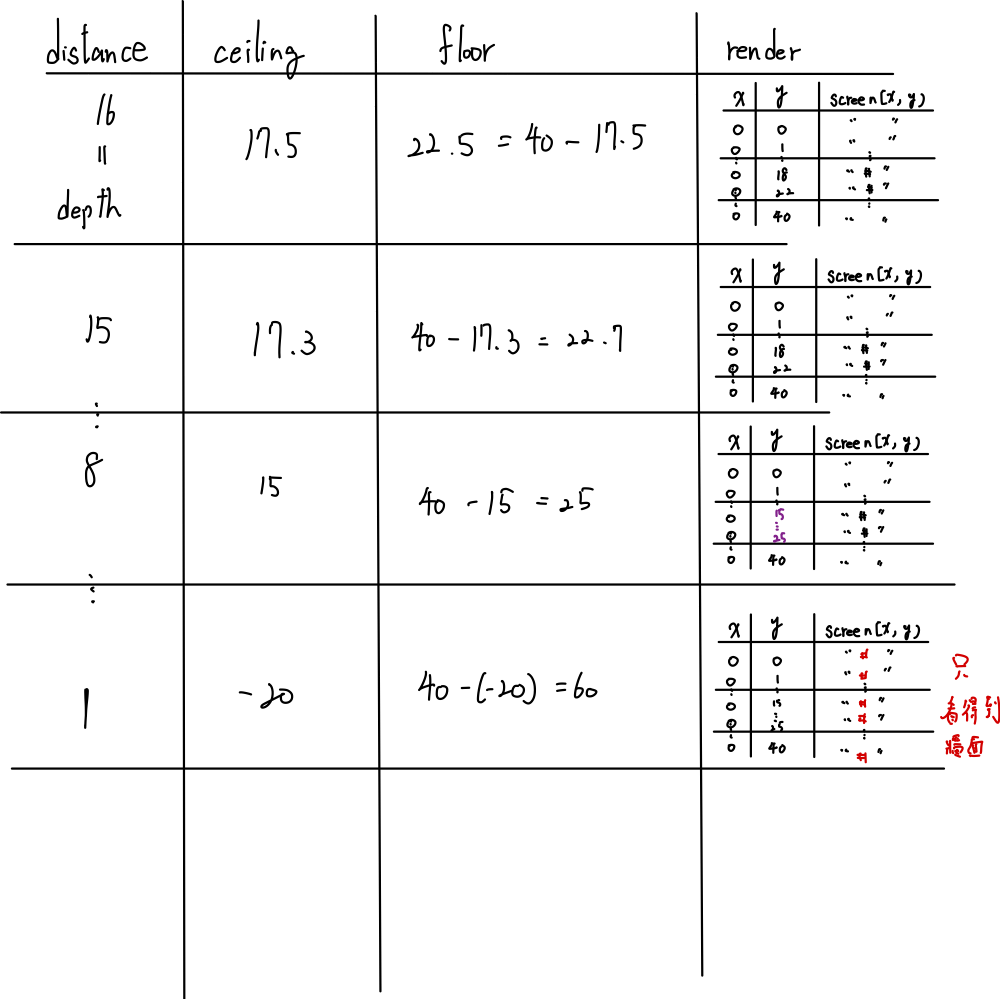

我們可以知道，當 fDistanceToWall = 16 (Depth) 時，
nCeiling = 17 、 nFloor = 22 ， 代表 當光超出地圖界線時，在 17 與 22 之間會看到牆壁 。
接著，我們可以把 fDistanceToWall 的值慢慢遞減，可以發覺:
nCeiling 越來越小， nFloor 越來越大 -> 牆壁高度越高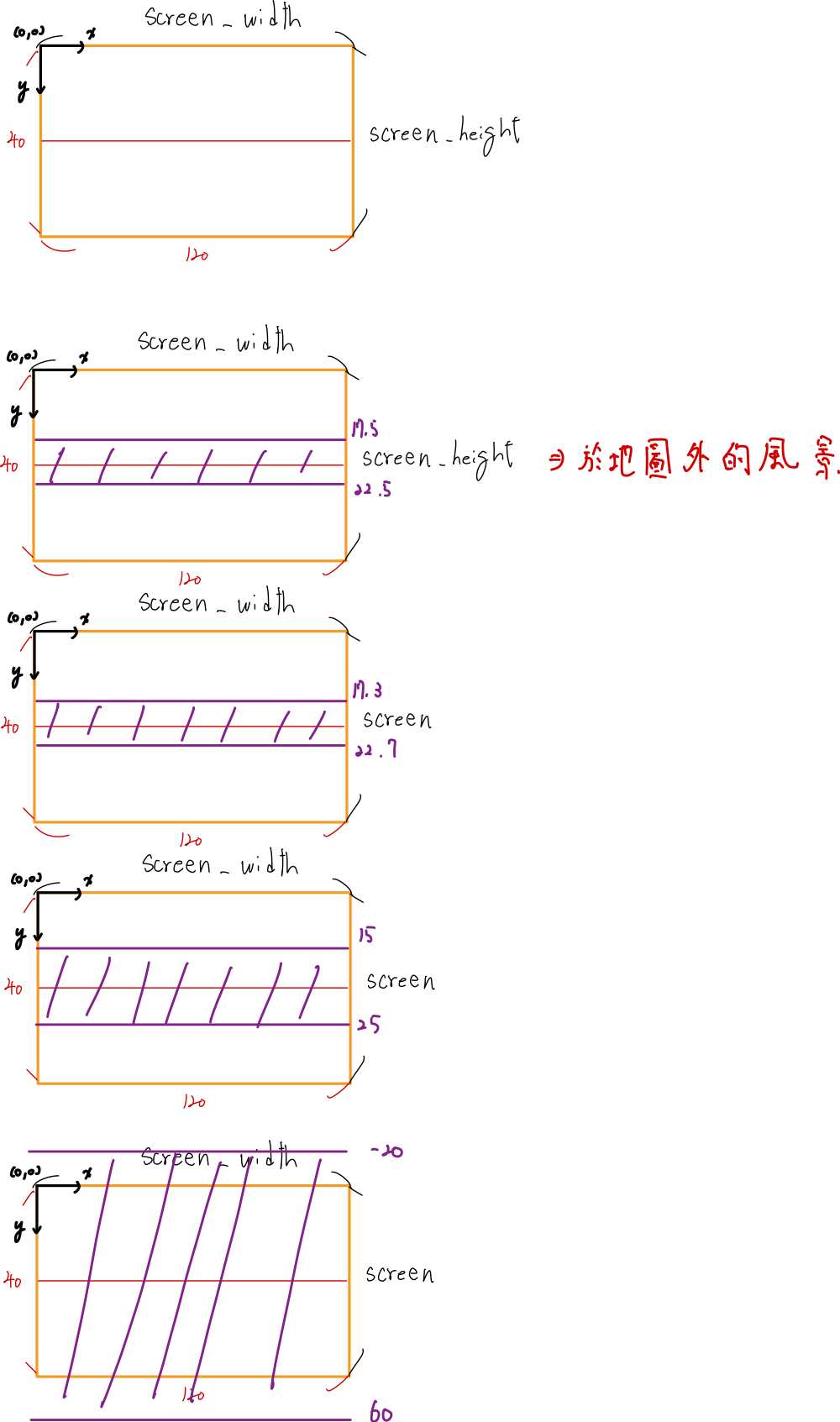

以上公式經由計算真的驗證了 fDistanceToWall 光行走的距離越近，玩家在該光線角度看到的牆越高，反之亦然，以下提供計算對照表以及圖: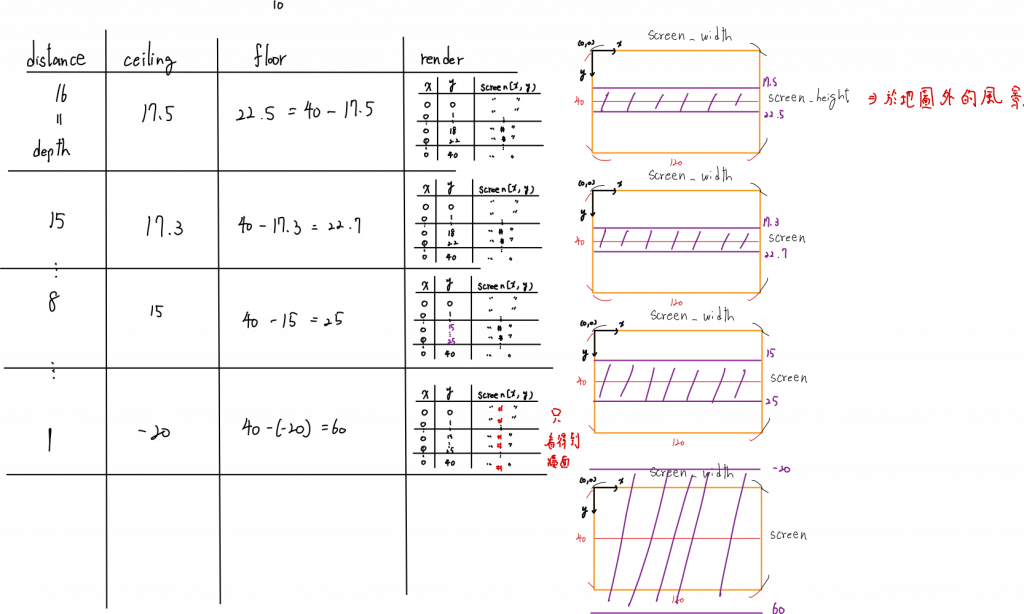

今日總結

• 透過 nCeiling 與 nFloor 的迭代觀察，我們找到了距離與牆高的規律
• fDistanceToWall 越大 → nCeiling 與 nFloor 越接近 → 牆壁變矮
• fDistanceToWall 越小 → nCeiling 與 nFloor 越遠 → 牆壁變高
• 這樣的結果驗證了**「距離決定牆高」**的直覺透視感

雖然目前還沒找到完整的數學推導與文獻，但規律已經能透過程式與手算驗證。
p.s. 其實有很多教學有提供關於**Projection Plane (screen)**牆壁高度計算的文章，會盡力去理解的~
明日我會嘗試用自己的觀點去解釋為什麼公式長這樣。
遊戲背後的數學，總是一步一步被拆解出來的。

我們繼續走下去~