線性模型

前一天我們學到了最直觀的 KNN 演算法，但他在預測時需要計算與所有訓練樣本的距離，這在數據量大時會變得非常緩慢。它並沒有真正「學習」到一個濃縮的、高效的決策模型

而線性模型 (linear model) 的核心思想，是試圖用一個線性的函數來進行預測。在二維空間中，這就是一條直線；在三維空間中，是一個平面；在更高維的空間中，則是一個超平面 (hyperplane)。

對於分類任務，這個超平面的作用就是一個決策邊界 (decision boundary)。所有在邊界一側的點被歸為一類，另一側的點被歸為另一類，數學形式可寫為

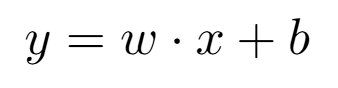
其中

• x 是我們的輸入特徵向量。

• w 和 b 就是模型需要「學習」的參數。它們共同定義了決策邊界的位置和方向。

線性模型的最大優點是預測速度極快。一旦 w 和 b 在訓練階段被確定，對於一個新的數據點 x，我們只需要做一次向量點積和加法，就能立刻得到分類結果，解決了 KNN 預測慢的問題。

HOG

但是，如果我們直接把一張圖片的原始像素值餵給一個簡單的線性模型，效果通常不會太好。因為像素值對物體的形狀、光照變化非常敏感。我們需要一種更穩健的特徵來描述物體的形狀。

方向梯度直方圖 (HOG) 是一種在電腦視覺領域中，被廣泛用於物體偵測（尤其是行人偵測）的特徵描述子。

它的核心思想是：物體的局部形狀和外觀，可以被其邊緣和角落的梯度方向分佈很好地描述，而無需關心精確的梯度強度。流程大致如下

1. 分割網格：將輸入影像分割成許多個小的、不重疊的單元格 (cell)，例如 8×8 像素。

2. 計算梯度: 在每個 cell 內部，計算每一個像素點的梯度（包括大小和方向）。

3. 統計直方圖：為每個 cell 建立一個梯度方向的直方圖。例如，將 0-180 度劃分成 9 個區間 (bins)，然後根據每個像素的梯度方向和大小，在對應的區間上投票。這個直方圖就代表了該 cell 內的邊緣方向分佈。

4. 區塊歸一化：將相鄰的多個 cell 組成一個更大的區塊 (block)，例如 2x2 個 cell。在 block 內部，將所有 cell 的直方圖串聯起來，並進行歸一化處理。這一步使得 HOG 對光照變化和對比度變化非常不敏感，極大地增強了其穩健性。

5. 生成描述子：最後，將影像中所有 block 的歸一化後的直方圖，全部串聯起來，就形成了一個長長的一維向量。這個向量就是整張圖片的 HOG 描述子。

SVM

支持向量機 (Support Vector Machine, SVM) 也是一種線性模型，但它的目標遠不止是找到一條能分開兩類數據的線，而是要找到那條最好的線：擁有最大間隔 (margin) 的決策邊界

• 間隔：決策邊界（實線）與兩邊虛線之間的「街道」寬度，就是間隔。SVM 的目標就是讓這條「街道」越寬越好。一個更寬的間隔意味著模型對未知數據的容忍度更高，泛化能力更強。

• 支持向量 (support vectors): 那些剛好落在「街道」邊緣上的數據點（被圈起來的點），被稱為支持向量。它們是定義決策邊界最關鍵的點。整個 SVM 模型只由這些支持向量決定，其他所有遠離邊界的點都不起作用。這使得 SVM 非常高效。

• 核技巧 (kernel trick): 如果數據本身是線性不可分的怎麼辦？SVM 透過「核技巧」，可以巧妙地將數據映射到一個更高維的空間，在那個高維空間中，數據就變得線性可分了。這使得 SVM 能夠處理非常複雜的非線性分類問題。

結合 HOG 與 SVM 的手寫數字辨識

import cv2
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_openml
from sklearn.metrics import classification_report
import numpy as np

print("正在從 OpenML 下載 MNIST 數據集...")
# 1. 載入 MNIST 數據集
X, y = fetch_openml('mnist_784', version=1, return_X_y=True, as_frame=False, parser='liac-arff')
print("數據集下載完成！")

# 為了加快執行速度，我們只使用部分樣本
sample_size = 10000
X_sample = X[:sample_size]
y_sample = y[:sample_size]

# 2. 計算 HOG 特徵
print("正在為所有圖片計算 HOG 特徵...")
hog_features = []
# 設定 HOG 描述子的參數
# 影像大小 28x28, 區塊大小 14x14, 區塊步長 7x7, 單元格大小 7x7
winSize = (28, 28)
blockSize = (14, 14)
blockStride = (7, 7)
cellSize = (7, 7)
nbins = 9
hog = cv2.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins)

for image in X_sample:
    # 將 784 維向量還原成 28x28 圖片
    img = image.reshape(28, 28).astype(np.uint8)
    # 計算 HOG 特徵
    features = hog.compute(img)
    hog_features.append(features.flatten()) # 攤平後加入列表

hog_features = np.array(hog_features)
print(f"HOG 特徵計算完成！特徵維度: {hog_features.shape}")

# 3. 分割數據集 (注意：現在的 X 是 HOG 特徵)
(train_X, test_X, train_y, test_y) = train_test_split(
    hog_features, y_sample, test_size=0.2, random_state=42)

# 4. 建立並訓練 SVM 模型
print("正在建立 SVM 模型...")
# C 是懲罰參數，gamma='scale' 是一個常用的核函數參數設定
model = SVC(kernel='rbf', C=10.0, gamma='scale')

print("正在訓練 SVM 模型 (這可能需要一些時間)...")
# SVM 的訓練過程是在尋找最佳決策邊界，計算量較大
model.fit(train_X, train_y)
print("SVM 模型訓練完成！")

# 5. 在測試集上進行預測
print("正在對測試集進行預測...")
predictions = model.predict(test_X)

# 6. 評估模型效能
print("\n模型評估報告:")
print(classification_report(test_y, predictions))

結果

模型評估報告:
              precision    recall  f1-score   support

           0       0.99      1.00      0.99       207
           1       0.98      1.00      0.99       216
           2       1.00      0.99      1.00       204
           3       0.98      0.98      0.98       192
           4       1.00      1.00      1.00       211
           5       1.00      0.97      0.99       176
           6       1.00      1.00      1.00       220
           7       0.98      1.00      0.99       216
           8       0.98      0.99      0.98       166
           9       0.99      0.97      0.98       192

    accuracy                           0.99      2000
   macro avg       0.99      0.99      0.99      2000
weighted avg       0.99      0.99      0.99      2000