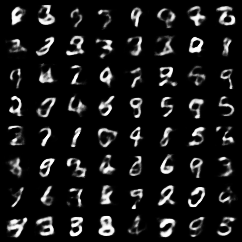自編碼器

自編碼器 1(AutoEncoder, AE) 是一種非監督式學習的神經網路，它的訓練目標極其簡單：讓輸出結果 x̂ 與輸入 x 盡可能地完全相同。

一個標準的 AE 可以分為兩個部分

1. 編碼器 (encoder) 網路的前半部分。它會接收原始的高維輸入數據，並將其壓縮成一個維度低得多的潛在表示 (latent representation) 或稱為編碼，通常用 z 來表示。

2. 解碼器：網路的後半部分。它會接收這個低維的編碼 z，並嘗試將其解壓縮，重建出與原始輸入一模一樣的數據。

整個網路的訓練，就是透過最小化重建損失 (reconstruction loss)，如輸入 x 和輸出 x̂ 之間的均方誤差來進行的。

為了能夠在經過一個低維的瓶頸後，還能成功地重建出原始數據，編碼器被迫去學習數據中最重要、最本質的特徵，並將其壓縮到 z 中。解碼器則被迫去學習如何僅僅根據這些本質特徵，來還原出完整的數據。

VAE

AE 雖然能重建數據，但它的生成能力很差。它的潛在空間 z 是不連續的、過擬合的，如果你在 z 空間中隨機取一個點，然後餵給解碼器，它很可能生成一張毫無意義的、模糊的圖像。

為了解決 AE 潛在空間不連續的問題，變分自編碼器 (Variational AutoEncoder, VAE) 因而誕生。 VAE 的核心改進在於：編碼器不再是直接輸出一組確定的編碼值 z，而是輸出兩個向量：一個均值向量 μ 和一個標準差向量 σ，模型結構如下

1. 機率編碼：我們假設，潛在空間 z 服從一個標準常態分佈 N(0, 1)。編碼器的任務，就是學習如何將輸入圖片 x，映射到一個特定的常態分佈 N(μ, σ^2) 上。

2. 重參數化技巧 (reparameterization trick)：我們不能直接從 N(μ, σ^2) 中進行採樣，因為「採樣」這個操作是不可微的，會導致梯度無法反向傳播。VAE 使用了一個巧妙的數學技巧：z = μ + ε * σ，其中 ε 是一個從標準常態分佈 N(0, 1) 中隨機採樣的噪點。這樣，梯度就可以順利地回傳給 μ 和 σ。

3. 機率解碼：解碼器接收這個採樣出的 z，並嘗試重建出原始圖片 x。

4. 特殊的損失函數：VAE 的損失函數由兩部分組成：

   a. 重建損失：與 AE 一樣，衡量輸入 x 與輸出 x̂ 的相似度。

   b. KL 散度 (Kullback–Leibler divergence)：用來衡量編碼器輸出的分佈 N(μ, σ^2) 與我們期望的標準常態分佈 N(0, 1) 之間的「距離」。這個損失項就像一個正規化器，強迫編碼器學習到的所有分佈，都向標準常態分佈看齊。

VAE 的潛在空間變得連續且結構化。在這個空間中，相近的點對應著相似的圖片。這意味著，在模型訓練好之後，我們可以丟掉編碼器，直接從標準常態分佈 N(0, 1) 中隨機採樣一個 z，然後將它餵給解碼器，生成一張全新的圖片。

用 VAE 生成手寫數字

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from torchvision.utils import save_image
import os

# --- 1. 設定超參數與設備 ---
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
input_size = 784
hidden_size = 400
latent_size = 20 # 潛在空間 z 的維度

batch_size = 128
num_epochs = 10
learning_rate = 0.001

# --- 2. 載入 MNIST 數據集 ---
train_dataset = datasets.MNIST(root='./data', train=True, transform=transforms.ToTensor(), download=True)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)

# --- 3. 定義 VAE 模型 ---
class VAE(nn.Module):
    def __init__(self, input_size, hidden_size, latent_size):
        super(VAE, self).__init__()
        # 編碼器
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.fc21 = nn.Linear(hidden_size, latent_size) # 均值 μ
        self.fc22 = nn.Linear(hidden_size, latent_size) # log(σ^2)
        # 解碼器
        self.fc3 = nn.Linear(latent_size, hidden_size)
        self.fc4 = nn.Linear(hidden_size, input_size)
        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()

    def encode(self, x):
        h = self.relu(self.fc1(x))
        return self.fc21(h), self.fc22(h)

    def reparameterize(self, mu, log_var):
        std = torch.exp(0.5 * log_var)
        eps = torch.randn_like(std)
        return mu + eps * std

    def decode(self, z):
        h = self.relu(self.fc3(z))
        return self.sigmoid(self.fc4(h))

    def forward(self, x):
        mu, log_var = self.encode(x.view(-1, input_size))
        z = self.reparameterize(mu, log_var)
        x_reconst = self.decode(z)
        return x_reconst, mu, log_var

# --- 4. 定義損失函數 ---
def vae_loss_function(recon_x, x, mu, log_var):
    # 重建損失 (使用二元交叉熵)
    BCE = nn.functional.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')
    # KL 散度
    KLD = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
    return BCE + KLD

# --- 5. 訓練模型 ---
model = VAE(input_size, hidden_size, latent_size).to(device)
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
print("開始訓練 VAE...")

for epoch in range(num_epochs):
    for i, (images, _) in enumerate(train_loader):
        images = images.to(device)
        recon_images, mu, log_var = model(images)
        loss = vae_loss_function(recon_images, images, mu, log_var)
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        if (i+1) % 100 == 0:
            print(f'Epoch [{epoch+1}/{num_epochs}], Step [{i+1}/{len(train_loader)}], Loss: {loss.item()/images.size(0):.4f}')
print("訓練完成！")

# --- 6. 生成新圖片 ---
with torch.no_grad():
    # 從標準常態分佈中隨機採樣
    z = torch.randn(64, latent_size).to(device)
    generated_images = model.decode(z).view(-1, 1, 28, 28)
    
    # 建立儲存結果的資料夾
    if not os.path.exists('results'):
        os.makedirs('results')
        
    save_image(generated_images, 'results/vae_generated.png')
    print("生成的新圖片已儲存至 'results/vae_generated.png'")

結果