接上一篇的講解，基於格的密碼學中所依賴的核心計算困難問題，第2類是平均情況困難問題，而針對平均情況的困難問題，會有以下2個問題:

1. 短整數解問題 (Short Integer Solution, SIS)
SIS 通常被描述為一個尋找短向量的問題，但它是在一個特定的數學結構下定義的。給定一個 m × n 的矩陣 A 和一個模數 q，SIS 旨在找到一個非零的短向量 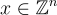，使得 。

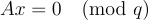給定一個矩陣 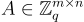和一個實數 β，找到一個非零向量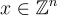
且 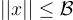，使得 。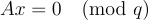

說明: SIS 問題與 SVP 密切相關。如果 A 的行向量可以看作是某個格的基，那麼 SIS 向量 x 就可以被視為這個對偶點格 (dual lattice) 中的一個短向量。SIS 的困難性保證了在特定條件下，很難從 A 找到一個非零且短的向量 x，這使得它成為數位簽章等密碼方案的基礎，例如 G-SIS 和 Dilithium。

2. 學習錯誤問題 (Learning with Errors, LWE)
LWE 是目前點陣密碼學中最重要、應用最廣泛的基礎問題之一。LWE 的核心概念是從帶有隨機誤差的線性方程組中，找出一個秘密向量。

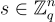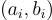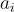給定一個秘密向量 ，生成多個帶有誤差的樣本 其中 是從 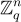中均勻隨機選取的向量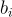， 的計算方式為 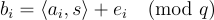。 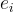是一個取自某個小分布 (例如高斯分布) 的隨機誤差。LWE 問題就是給定這些樣本 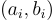，找出秘密向量 s。

說明: 如果沒有誤差 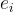，這個問題就是一個簡單的線性代數問題，可以很容易地求解。然而，加入了隨機的小誤差後，這個問題就變得非常困難。Regev 證明了，在最壞情況下，解決 LWE 問題等價於解決某些點陣上的近似 SVP (Approximate SVP) 問題，而這些問題在量子電腦上也是困難的。由於這個強大的還原證明，LWE 成為了構建各種密碼方案的基石，包括同態加密、金鑰交換和公鑰加密等。Kyber 是一種基於 LWE 的金鑰交換協議，被美國 NIST 選為後量子密碼標準，其安全性就建立在 LWE 的困難性上。