複雜性和密碼學中許多關於格的現代工作依賴於格上的高斯類概率分佈,稱為離散高斯。
我會在這裡簡單講一下相關的定義。
高斯分佈 (Gaussians):
對於任何正整數 n 和實數 s>0(省略時默認為 s=1),定義一個高斯函數(Gaussian function)為: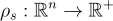 其參數為 s:
其參數為 s: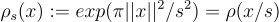
注意 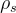 在
在 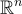 的旋轉下是不變的,且
的旋轉下是不變的,且 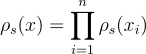 。
。
在"連續"的高斯分佈 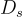 的參數為 s,在
的參數為 s,在 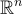 上的概率密度函數與
上的概率密度函數與 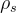 成正比,即
成正比,即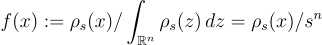 。
。
對於格陪集 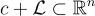 和參數 s>0,離散高斯概率分佈
和參數 s>0,離散高斯概率分佈 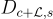 簡單地是高斯分佈限制在陪集上:
簡單地是高斯分佈限制在陪集上: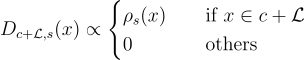
平滑參數:
Micciancio 和 Regev [MR04] 引入了一個非常重要的量,稱為格的平滑參數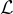 。
。
非正式地說,這是高斯"模糊"所需的量,以"平滑掉"格的幾乎所有離散結構。或者,可以將其視為最小的寬度 s>0,使得每個陪集 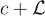 的高斯質量
的高斯質量 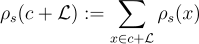 幾乎相同,最多只有小的相對誤差。
幾乎相同,最多只有小的相對誤差。
形式上,平滑參數 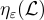 由容差 ε>0 參數化,並使用對偶格定義為滿足
由容差 ε>0 參數化,並使用對偶格定義為滿足 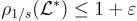 的最小 s>0。
的最小 s>0。
這個條件可以用來形式化和證明上述"平滑"性質。出於本調查的目的,會省略 ε 並隱含地假設它非常小,例如格維度 n 中的可忽略函數 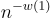 。
。
平滑參數與其他標準格量密切相關
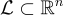 ,有
,有 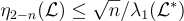 。
。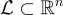 和
和 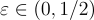 ,有
,有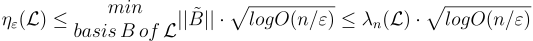 ,
,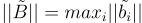 表示有序基
表示有序基 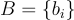 的 Gram-Schmidt 正交化向量
的 Gram-Schmidt 正交化向量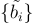 的最大長度。
的最大長度。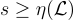 時,離散高斯分佈
時,離散高斯分佈 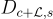 在許多重要方面與連續高斯
在許多重要方面與連續高斯 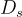 非常相似。例如,它們的矩和尾部幾乎相同,且獨立離散高斯的和是離散高斯。
非常相似。例如,它們的矩和尾部幾乎相同,且獨立離散高斯的和是離散高斯。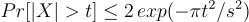 。
。更一般地, 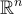 上的隨機向量 x 是參數為 s 的次高斯,如果對於所有單位向量
上的隨機向量 x 是參數為 s 的次高斯,如果對於所有單位向量 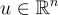 ,每個邊際
,每個邊際 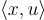 都是次高斯的。不難證明,具有共同參數 s 的獨立次高斯隨機變量或向量的串聯本身就是參數為 s 的次高斯向量。
都是次高斯的。不難證明,具有共同參數 s 的獨立次高斯隨機變量或向量的串聯本身就是參數為 s 的次高斯向量。
參數為 s 的次高斯分佈的例子包括任何幅度有界於 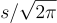 的對稱隨機變量;任何格 LL 上的連續高斯
的對稱隨機變量;任何格 LL 上的連續高斯 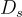 和離散高斯
和離散高斯 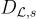 ;以及當
;以及當 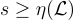 時,任何格陪集上的離散高斯
時,任何格陪集上的離散高斯 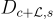
參考資料:
[Ban93] W. Banaszczyk. New bounds in some transference theorems in the geometry of numbers.
Mathematische Annalen, 296(4):625–635, 1993.
[Ban95] W. Banaszczyk. Inequalites for convex bodies and polar reciprocal lattices in Rn
. Discrete &
Computational Geometry, 13:217–231, 1995.
[AR04] D. Aharonov and O. Regev. Lattice problems in NP ∩ coNP. J. ACM, 52(5):749–765, 2005.
Preliminary version in FOCS 2004.
[MR04] D. Micciancio and O. Regev. Worst-case to average-case reductions based on Gaussian
measures. SIAM J. Comput., 37(1):267–302, 2007. Preliminary version in FOCS 2004.
[Reg05] O. Regev. On lattices, learning with errors, random linear codes, and cryptography. J. ACM,
56(6):1–40, 2009. Preliminary version in STOC 2005.
[Pei07] C. Peikert. Limits on the hardness of lattice problems in `p norms. Computational Complexity,
17(2):300–351, May 2008. Preliminary version in CCC 2007.
