主題

今天主要要講解

• 基本合法性檢查（數字範圍、位置）
• 如何透過基本合法性檢查與 Backtrack 演算法生成題目

Sudoku 的合法性檢查

Sudoku 的基本規則：

• 每一列（Row）不可重複出現相同的數字。
• 每一行（Column）不可重複出現相同的數字。
• 每一個 3x3 區塊（Box）不可重複出現相同的數字。

此外，數字必須介於 1 到 9 之間，0 代表空格。

// 檢查 row, col 位置是否可以放置 num
func (board *Board) isSafe(row, col, num int) bool {
	// 檢查行與列是否有放相同的值
	for i := 0; i < BoardSize; i++ {
		if board.Cells[row][i].Value == num || board.Cells[i][col].Value == num {
			return false
		}
	}

	// 檢查 Box 內是否有相同的值
	boxRow := (row / BoxSize) * BoxSize
	boxCol := (col / BoxSize) * BoxSize
	for rc := 0; rc < BoxSize; rc++ {
		for bc := 0; bc < BoxSize; bc++ {
			if board.Cells[boxRow+rc][boxCol+bc].Value == num {
				return false
			}
		}
	}

	// 檢查 num 值介於 1 到 9
	if num < 1 || num > 9 {
		return false
	}
	return true
}

使用 Backtracking 生成題目

什麼是 Backtracking？

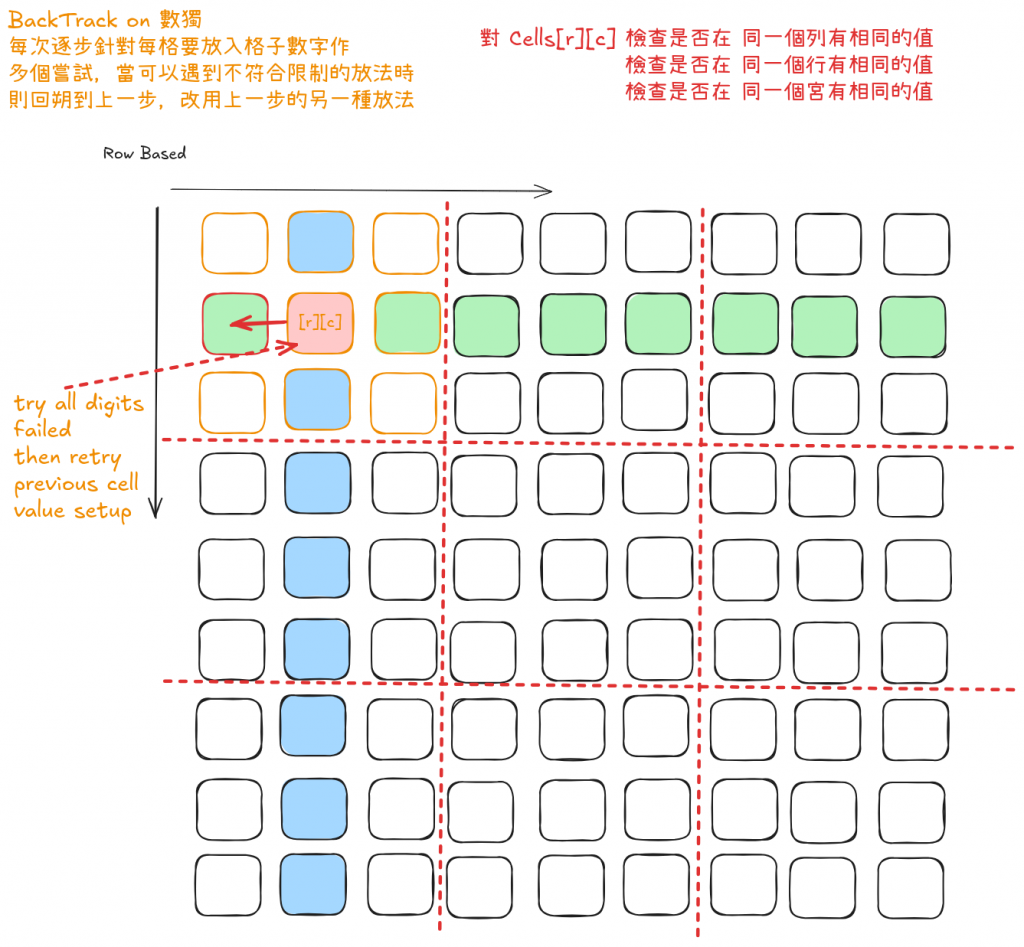
Backtracking（回溯演算法）常用於解決排列組合與棋盤類問題。其核心概念是「嘗試 → 檢查 → 回退」，適合用於 Sudoku 這類需要逐步填入數字並檢查合法性的題目。

圖解 backtracking for Sudoku

Sudoku 題目生成流程

1. 建立一個空的 9x9 盤面。
2. 依序填入數字（1–9），每一步都檢查是否合法。
3. 若某步無法繼續，則回退到上一步，嘗試其他數字。
4. 直到填滿整個盤面 → 得到一份完整解答。
5. 根據需要的難度，移除部分格子形成題目。

1. 生成解法

// presetBoard - 填滿格子
func (board *Board) presetBoard() bool {
	row, col, foundEmpty := -1, -1, false
	// 找到第一個非空的格子來填
	for r := 0; r < BoardSize && !foundEmpty; r++ {
		for c := 0; c < BoardSize && !foundEmpty; c++ {
			if board.Cells[r][c].Value == 0 && board.Cells[r][c].Type != Preset {
				row, col, foundEmpty = r, c, true
			}
		}
	}

	// 當所有都填滿了回傳 true
	if !foundEmpty {
		return true
	}

	// 隨機取值出來填寫
	for _, digit := range digitsShuffled() {
		// 確認 digit 是否可以填入 row, col
		if board.isSafe(row, col, digit) {
			// 先填入 row, col 為 digit
			board.Cells[row][col].Type = Preset
			board.Cells[row][col].Value = digit
			// 如果格子填滿則回傳 true
			if board.presetBoard() {
				return true
			}
			// 否則把 row, col 回朔
			board.Cells[row][col].Type = Empty
			board.Cells[row][col].Value = 0
		}
	}
	return false
}

// GenerateSolution - 產生解法
func (board *Board) GenerateSolution() {
	// 填入解法
	board.presetBoard()
}

2. 生成空格

// MakePuzzleFromSolution - 建立題目
func (board *Board) MakePuzzleFromSolution(targetClues int) {
	puzzle := board.Clone()
	order := coordsShuffled()
	for _, rc := range order {
		if puzzle.presetedCount() <= targetClues {
			break
		}
		r, c := rc[0], rc[1]
		if puzzle.Cells[r][c].Type == Empty {
			continue
		}
		tmp := puzzle.Cells[r][c]
		puzzle.Cells[r][c].Type = Empty
		puzzle.Cells[r][c].Value = 0
		if puzzle.hasUniqueSolution() {
			// 不是唯一解 → 復原
			puzzle.Cells[r][c].Type = tmp.Type
			puzzle.Cells[r][c].Value = tmp.Value
		}
	}
	board = &puzzle
}

撰寫測試

合法性解查測試

func TestIsSafe(t *testing.T) {
	type coord struct {
		Row int
		Col int
	}
	tests := []struct {
		name        string
		targetCoord coord
		targetValue int
		setup       func() *Board
		want        bool
	}{
		{
			name: "check if board is safe to put 1, 2 with value 9, should be false, for setup board.Cells[1][1].Value=9",
			targetCoord: coord{
				Row: 1,
				Col: 2,
			},
			targetValue: 9,
			setup: func() *Board {
				board := NewBoard()
				board.Cells[1][1].Type = Preset
				board.Cells[1][1].Value = 9
				return board
			},
			want: false,
		},
		{
			name: "check if board is safe to put 2, 5 with value 9, should be true, for setup board.Cells[1][1].Value=9, boards.Cells[4][3].Value = 9",
			targetCoord: coord{
				Row: 2,
				Col: 5,
			},
			targetValue: 9,
			setup: func() *Board {
				board := NewBoard()
				board.Cells[1][1].Type = Preset
				board.Cells[1][1].Value = 9
				board.Cells[4][3].Type = Preset
				board.Cells[4][3].Value = 9
				return board
			},
			want: true,
		},
	}
	for _, tt := range tests {
		t.Run(tt.name, func(t *testing.T) {
			board := tt.setup()
			got := board.isSafe(tt.targetCoord.Row, tt.targetCoord.Col, tt.targetValue)
			assert.Equal(t, tt.want, got)
		})
	}
}

題目生成檢查

func TestMakePuzzleFromSolution(t *testing.T) {
	tests := []struct {
		name           string
		targetClues    int
		wantCluesCount int
		setup          func() *Board
	}{
		{
			name:           "generate puzzle with Easy Level",
			targetClues:    int(Easy),
			wantCluesCount: int(Easy),
			setup: func() *Board {
				board := NewBoard()
				board.GenerateSolution()
				return board
			},
		},
		{
			name:           "generate puzzle with Medium Level",
			targetClues:    int(Medium),
			wantCluesCount: int(Medium),
			setup: func() *Board {
				board := NewBoard()
				board.GenerateSolution()
				return board
			},
		},
		{
			name:           "generate puzzle with Hard Level",
			targetClues:    int(Hard),
			wantCluesCount: int(Hard),
			setup: func() *Board {
				board := NewBoard()
				board.GenerateSolution()
				return board
			},
		},
	}

	for _, tt := range tests {
		t.Run(tt.name, func(t *testing.T) {
			board := tt.setup()
			board.MakePuzzleFromSolution(tt.targetClues)
			got := board.presetedCount()
			assert.Equal(t, tt.wantCluesCount, got)
		})
	}
}

github action 測試結果

https://github.com/leetcode-golang-classroom/sudoku-game/actions/runs/17518677864/job/49759560227

驗收條件

• 能夠判斷任意 (row,col,val) 是否違反 列/行/宮。
• 能對載入的題面做 整盤合法 檢查（允許空格）。
• 能產生一份題目（依難度控制線索數），且 具唯一解。

🏁 今日收穫

• 完成 規則檢查 的最小可用集合（單點/整盤）。
• 建立「先解後挖 + 唯一解驗證」的題目生成管線。
• 知道效能瓶頸在「唯一解檢查」，並用 計數早停 改善。

明日預計

Sudoku 遊戲 Ebiten 基本盤面繪製

在前幾篇文章中，我們已經完成了 Sudoku 的盤面資料結構、題目載入、合法性檢查，以及利用 Backtracking 生成題目。這些都屬於「資料面」的準備。
接下來，我們將邁向遊戲的「畫面呈現」，也就是使用 Ebiten 來繪製 Sudoku 的 9x9 棋盤。