誤差學習 (Learning With Errors, LWE)
Regev 在 2005 年的一項非常重要的工作中引入了平均情況的誤差學習（LWE）問題，它是 SIS 問題的「支持加密」的對應物。實際上，這兩個問題在語法上非常相似，並且可以有意義地視為彼此的對偶。這裡會詳細描述 LWE、其硬度以及一個基於 LWE 的基本密碼系統。
定義
LWE 由正整數 n 和 q，以及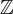 
上的誤差分佈 χ 來參數化。具體來說，n 和 q 可以認為與 SIS 中的大致相同，而 χ 通常取參數為 
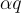（對於某個 
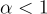）的離散高斯分佈，這通常被稱為相對「誤差率」。
Regev 的原始工作 考慮了連續高斯分佈，然後通過四捨五入到最近的整數將其離散化。雖然這並不完全是真正的離散高斯分佈，但在[Pei10] 中的一個定理的特殊情況表明，一個稍微不同的隨機化離散化方法可以做到這一點。
定義 LWE 分佈:
對於稱為秘密的向量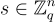 
，在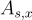 
上的 LWE 分佈 
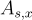是通過均勻隨機選擇 
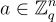，選擇 
，並輸出 
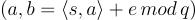來取樣。
值得一提的是，LWE 是「帶噪聲學習奇偶校驗」（learning parities with noise）的推廣，這是當 q=2 且 χ 是 {0,1} 上的伯努利分佈時的特殊情況。
LWE 問題有兩個主要版本:
定義 -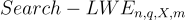 
:
給定 m 個從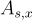 
抽取的獨立樣本 
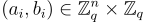，其中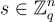 
是均勻隨機的（對所有樣本固定），找到 s。
定義 -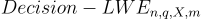 
。給定 m 個獨立樣本 
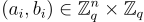，其中每個樣本根據以下之一分佈：(1) 對於均勻隨機的 
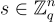（對所有樣本固定）的 
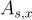，或 (2) 均勻分佈，區分是哪種情況（以不可忽略的優勢）。
強調關於搜尋和判定 LWE 的幾個有用觀察：
如果沒有來自 χ 的誤差項，這兩個問題都很容易解決，因為可以通過高斯消去法從 LWE 樣本中高效地恢復 s。（在判定 LWE 的均勻情況下，以高機率不存在解 s。）
與 SIS 類似，將給定的樣本組合成矩陣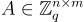 
（其列是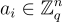向量 
) 和向量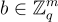
（其項是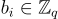 
) 通常很方便，因此對於 LWE 樣本，有
,
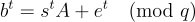其中 
。在判定 LWE 的均勻情況下，b 是均勻隨機的並且獨立於 A。
對於後續的密碼學方案，一個有用的約定是：SIS 在右邊乘以秘密，LWE 在左邊乘以秘密。
,
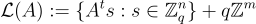目標是找到那個格向量。（在均勻情況下，b 以極高機率遠離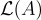 
中的所有點。）此外，不難驗證，在方程式 
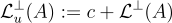和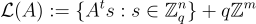 
中分別定義的 SIS 格和 LWE 格在縮放因子 q 下是對偶的，即 
。
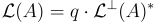標準形式
類似於 SIS，LWE 問題也有一個標準形式，其中秘密 s 的座標是從誤差分佈 χ（模 q）中獨立選擇的。如下文所述，使用這種形式可以為某些密碼學構造帶來顯著的效率提升。Applebaum 等人 [ACP509]（遵循 [MR09]）證明，對於搜尋或判定變體，標準形式至少與秘密的任何分佈（例如均勻分佈）的相同變體一樣難，最多在樣本數量 m 上有小的差異。證明這一點的歸約是為 SIS 描述的歸約的輕微擴展:
給定一個實例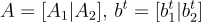
其中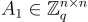 
是可逆的且 b1∈Zqn，
將其轉換為實例
Aˉ=−A1−1⋅A2,bˉt=b1tAˉ+b2t.
如前所述，Aˉ 是均勻隨機的，因為 A2 獨立於 A1。現在觀察到，當輸入來自 LWE 分佈時，每個 bit=stAi+eit（對於某個 s∈Zqn），其中每個 ei 的項是從 χ 獨立抽取的，所以有
bˉt=stA1⋅Aˉ+e1tAˉ+stA2+e2t
=e1tAˉ+e2t.
也就是說，實例 Aˉ, bˉ 來自秘密為 e1 的 LWE 分佈，找到 e1 就能得到原始秘密 st=(b1t−e1t)⋅A1−1。同樣，對於判定問題，當 b 是均勻隨機的且獨立於 A 時，立即得出 bˉ 是均勻隨機的且獨立於 Aˉ。
使用標準形式，LWE 甚至可以在語法上看作與 SIS 的標準形式相同，但參數對應於單射函數而非滿射函數：SIS 關注滿射函數，將短的 x∈Zm 映射到 [In∣Aˉ]⋅x∈Zqn，而 LWE 處理單射函數，將短的 e∈Zm 映射到 [Aˉt∣Im−n]⋅e∈Zqm−n）然而，可以構造的密碼學物件以及可以證明的關於其硬度的方面，單射性和滿射性之間存在主要的質性差異。
硬度
Regev 證明了以下關於 LWE 的最壞情況硬度定理
定理2 - [Reg05]
對於任何 m=poly(n)，任何模數 q≤2poly(n)，以及任何參數為 αq≥2n（其中 0<α<1）的（離散化）高斯誤差分佈 χ，求解判定-LWE n,q,χ,m 問題至少與在任意 n 維格上量子求解 GapSVPγ 和 SIVPγ 一樣難，其中某個 γ=O~(n/α)。
請注意，與 SIS 的最壞情況硬度定理一樣 (在上一篇文章提及的定理1)，m 和 q 的精確值（除了其下界 2n/α) 在最終的硬度保證中基本上不起作用。然而，近似因子 γ 隨著 LWE 問題的逆誤差率 1/α 而變差。
定理 A 的證明是通過給出一個量子多項式時間歸約，該歸約使用 LWE 的預言機在最壞情況下求解 GapSVPγ 和 SIVPγ，從而將任何（無論是經典還是量子的）求解 LWE 的演算法轉換為求解格問題的量子演算法。歸約的量子性質是有意義的，因為除了通用的量子加速外，目前沒有已知的量子演算法能顯著優於經典演算法來解決 GapSVPγ 或 SIVPγ。不過，擁有一個完全經典的歸約來進一步增強對 LWE 硬度的信心將非常有用。Peikert [Pei09] 在 2009 年給出了這樣一個歸約，並將在下面討論。
在 [Reg05] 中，上述定理的證明分為兩個主要部分:
首先，通過量子歸約證明搜尋-LWE 至少與最壞情況的格問題一樣難。這個歸約包含兩個主要子部分：
(a) 使用搜尋-LWE 的預言機以及參數為 r 的 LL 上離散高斯取樣的來源，可以經典地在對偶格 L∗ 上求解有界距離解碼 BDD，距離在 d≈αq/rd≈αq/r 內。這是通過將 BDD 實例與高斯樣本結合以產生正確分佈的 LWE 樣本來實現的，這些樣本的底層秘密（由預言機揭示）使能夠計算 BDD 的解。
(b) 使用在 L∗ 上距離 d 內的 BDD 預言機，可以量子地生成參數為 r′≈n/d 的 L 上的離散高斯樣本。這使用量子計算來「反計算」BDD 實例的已知解，這使能夠建立一個特定的量子態。對這個態計算量子傅立葉變換並測量，就得到一個離散高斯樣本。
請注意，對於來自第一個子部分的 d 值，在第二個子部分中有 r′≤r/2，因為 αq≥2n。完整的歸約迭代這兩個步驟，生成參數連續變窄的離散高斯樣本，直到步驟停止工作，此時在 L 上有了非常窄的離散高斯樣本，這很容易產生 SIVP 和 GapSVP 的解。
其次，通過基本的經典歸約證明判定-LWE 等價於搜尋-LWE（在樣本數量 m 上最多有一些多項式級的膨脹）。最初，這種等價性僅適用於多項式有界的素數模數 q=poly(n)，推廣了早期針對 q=2 情況的證明 [BFKL93]。隨後，它被改進為適用於基本上任何模數 [Pei09, ACPS09, MM11, MP12, BLP+13]，就算是指數級大的合數模數。
密碼系統
在 [Reg05] 中，Regev 還給出了一個新的公鑰密碼系統，其語義安全性可證明基於誤差率為 α=Ω~(1/n) 的 LWE 問題，因此也基於 γ=O~(n3/2) 的 GapSVPγ 或 SIVPγ 的假設量子硬度。與 Ajtai-Dwork [AD97] 和 Regev 對其的改進 [Reg03] 相比，基於 LWE 的密碼系統有兩個顯著特點：
通用性：底層的最壞情況問題 GapSVPγ 和 SIVPγ 看起來比唯一最短向量問題 uSVPγ 更少「結構化」。
改進的效率：公鑰僅為 O~(n2) 位元（相對於 O~(n4)），而私鑰和密文對於每個加密的消息位元僅為 O~(n) 位元（相對於 O~(n2)）。
此外，在多用戶設置中，每個用戶的公鑰可以減少到 O~(n) 位元，使用在所有用戶之間共享的 O~(n2) 位元可信隨機性。
目前尚不清楚如何為 [AD97, Reg03], 實現這種共享，雖然 Ajtai [Ajt05] 後來給出了一種允許共享的不同風格的密碼系統，但沒有已知的最壞情況安全性證明。
在高層次上，Regev 基於 LWE 的密碼系統的構造和安全性證明強烈讓人想起 Ajtai-Dwork：私鑰是一個隨機向量 s∈Zqn，公鑰是秘密 s 的幾個 LWE 樣本 (ai,bi)。通過在公鑰中添加樣本的隨機子集來加密一個位元，然後適當地將消息位元隱藏在結果的最後一個座標中，使得密文要麼「接近於」要麼「遠離於」正交於 (−s,1) 的子空間。使用秘密 s，可以通過區分這兩種情況來解密。語義安全性通過考慮一個思想實驗來證明，在該實驗中公鑰是「畸形」的，即它由沒有底層秘密的均勻隨機樣本組成。假設 LWE 的硬度，沒有對手能區分這樣的密鑰與正確形成的密鑰。此外，在此類畸形密鑰下的加密是「有損的」，因為生成的密文在統計上獨立於消息位元，因此對手在區分 0 的加密和 1的加密方面沒有優勢。
iThome鐵人賽
看影片追技術