硬度結果
接上一篇的講解，繼 [Reg05] 之後，有以下幾項工作為 LWE 提供了額外的硬度定理，
例如，在經典歸約下、針對「洩漏」的秘密、針對更小的誤差和模數等。

經典硬度:
Peikert [Pei09] 的一項工作部分地「去量子化」了 Regev 的量子最壞情況歸約 [Reg05]（來自上一篇中的定理2）。特別是，這是第一個基於一般格上問題的最壞情況經典硬度來產生公鑰加密的工作，相對於 [AD97, Reg03] 中具有「唯一」最短向量的結構化格。更具體地說，Peikert 證明，對於相同的 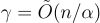因子，誤差率為 α 的 LWE 在經典上至少與最壞情況的 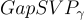一樣難。然而，有兩個主要警告:

• 經典歸約僅適用於 GapSVP，不適用於 SIVP，而量子歸約對兩個問題都適用。
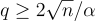• 歸約要求 LWE 問題的模數 q≥2n/2 是指數級大的，而量子歸約適用於任何模數 。（經典歸約可以修改為適用於小至 q=poly(n) 的模數，但這是針對 GapSVP 的一個非標準變體。）

大模數意味著 LWE 樣本需要更多位元來表示，從而導致更大的密鑰大小和效率更低的密碼方案。然而，它似乎並不限制可以從 LWE 構造的種類的密碼學應用。

緊隨 [Pei09] 之後，Lyubashevsky 和 Micciancio [LM09] 在其主要思想的基礎上，在經典歸約下證明了 GapSVP、uSVP 和 BDD 問題在小 poly(n) 近似因子內的等價性。特別是，這意味著最初基於 uSVP 的 Ajtai-Dwork 密碼系統實際上也可以基於 GapSVP。

幾年後，Brakerski 等人 [BLP+13] 給出了 LWE 的一個通用維度-模數權衡，大致上說，對於特定的誤差率 α，硬度幾乎完全由 nlogq 決定，而不是由 n 和 q 的特定選擇決定，只要 q 從下方被某個小的多項式所界定。例如，使用 Peikert 的結果，即 n 維格上的 GapSVP 經典歸約到維度 n、模數 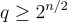的 LWE，根據 [BLP+13]，相同的 GapSVP 問題經典歸約到維度 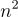、模數 q=poly(n) 的 LWE。[BLP+13] 的歸約深受全同態加密文獻（例如 [BV11b, BGV12, Bra12];）中開發的「密鑰切換」和「模數縮減」等技術的影響，但由於需要生成正確的 LWE 分佈而不僅僅是具有小誤差項的樣本，因此在技術上更加複雜。

Robustness:
LWE 是一個非常 Robust 的問題，這意味著即使攻擊者學到了關於秘密和誤差的額外資訊，它仍然保持困難。例如，Goldwasser 等人 [GKPV10] 表明，具有「弱」秘密的 LWE — — 即對手學到關於秘密的一些有界資訊，或秘密的一個難於反轉的函數 — — 與具有「完美」秘密的 LWE 一樣難，儘管對於更小的維度 nn 和誤差率 αα。他們利用這一事實給出了一個對不完美或洩漏私鑰魯棒的對稱密鑰加密方案。類似地，Dodis 等人 [DGK+10] 從 LWE 給出了一個公鑰加密方案，該方案對私鑰的任何計算上難於反轉的函數的洩漏具有魯棒性。最後，幾項工作 [BF11, OPW11, AP12, BLP+13, LPSS14] 給出了相對緊密的歸約，表明即使揭示秘密和誤差上的一個或多個（在整數上的）線性關係，LWE 在維度和誤差率上最多只有小的損失的情況下仍然保持困難。

替代誤差和小參數
在獨立的工作中，Döttling 和 Müller-Quade [DM13] 以及 Micciancio 和 Peikert [MP13] 也考慮了具有非高斯且可能很小的誤差的 LWE，例如，在區間上均勻的分佈。此類分佈在演算法上比高斯分佈更容易取樣，因此在實際實現中可能更合適。另一個動機是 Arora 和 Ge [AG11] 的演算法攻擊，該攻擊表明，對於來自大小為 d 的域的誤差，如果攻擊者被給予足夠多的 LWE 樣本，則可以在時間和空間上大致以 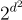求解 LWE。儘管 [DM13, MP13] 的結果的精確陳述幾乎完全不相交，但它們的質性風格和技術非常相似。為了具體起見，給出關於後者的一些細節。

[MP13] 的工作表明，對於非高斯誤差分佈（例如均勻分佈），即使其支集很小（甚至可以小到 {0,1}），只要攻擊者可用的樣本數量 m 被適當限制，LWE 仍然保持困難。請注意，對於小支集，考慮到上面提到的 Arora-Ge 攻擊 [AG11]，某種樣本限制是必要的。

例如，對於二元誤差，樣本數量被限制為 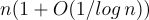，而對於大小為 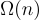的支集，樣本數量可以大到 O(n)。雖然前者的樣本限制不足以支持任何已知的 LWE 密碼學應用，但後者對於某些用途來說足夠大。[MP13] 的主要定理依賴於標準 LWE 對於足夠大的高斯誤差的假設硬度，並且在稍大的維度上。它使用了一個「有損性」論證，非常類似於 [PW08] 的主要思想，該論證表明，如果樣本 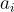是根據底層的（標準）LWE 分佈生成的，而不是均勻隨機的，那麼具有小誤差的搜尋 LWE 是資訊理論上不可解的。由於標準 LWE 分佈與均勻分佈不可區分，因此如果不破壞標準的判定 LWE，就不能破壞 LWE 的小誤差版本。

參考資料:
[GKPV10] S. Goldwasser, Y. T. Kalai, C. Peikert, and V. Vaikuntanathan. Robustness of the learning with errors assumption. In ICS, pages 230–240. 2010.

[DGK+10] Y. Dodis, S. Goldwasser, Y. T. Kalai, C. Peikert, and V. Vaikuntanathan. Public-key encryption schemes with auxiliary inputs. In TCC, pages 361–381. 2010.

[BF11] D. Boneh and D. M. Freeman. Linearly homomorphic signatures over binary fields and new tools for lattice-based signatures. In Public Key Cryptography, pages 1–16. 2011.

[OPW11] A. O’Neill, C. Peikert, and B. Waters. Bi-deniable public-key encryption. In CRYPTO, pages 525–542. 2011.

[AP12] J. Alperin-Sheriff and C. Peikert. Circular and KDM security for identity-based encryption. In
Public Key Cryptography, pages 334–352. 2012.

[BLP+13] Z. Brakerski, A. Langlois, C. Peikert, O. Regev, and D. Stehle. Classical hardness of learning with errors. In STOC, pages 575–584. 2013.

[LPSS14] S. Ling, D. H. Phan, D. Stehle, and R. Steinfeld. Hardness of ´ k-LWE and applications in traitor tracing. In CRYPTO, pages 315–334. 2014.

[DM13] N. Dottling and J. M ¨ uller-Quade. Lossy codes and a new variant of the learning-with-errors problem. In EUROCRYPT, pages 18–34. 2013.

[MP13] D. Micciancio and C. Peikert. Hardness of SIS and LWE with small parameters. In CRYPTO, pages 21–39. 2013.

[AG11] S. Arora and R. Ge. New algorithms for learning in presence of errors. In ICALP (1), pages 403–415. 2011.

[PW08] C. Peikert and B. Waters. Lossy trapdoor functions and their applications. SIAM J. Comput., 40(6):1803–1844, 2011. Preliminary version in STOC 2008.