Ring-SIS
受 NTRU 密碼系統 [HPS98] 背後思想的啟發，Micciancio [Mic02] 引入了 Ajtai 的 SIS 問題及其從定義 4.1.1 衍生的關聯函數 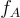的一個緊湊的基於環的類比。這個類比後來被稱為環-SIS問題。這裡定義這個問題，描述它與 SIS 的聯繫，並綜述其在底層環中相對於理想格（ideal lattices）上最壞情況問題的硬度。

定義
環-SIS 問題由以下參數化:

• 一個環 R:
  通常取為形式為 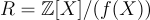的 n 次多項式環，例如 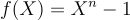（如在 [Mic02] 中），或 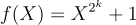（如在 [LMPR08] 中）。注意，R 的元素可以規範地由其模 f(X) 的剩餘表示，這些剩餘是次數小於 n 的整係數多項式。賦予 R 一個範數
  || . ||，它不一定是參數係數向量的範數

• 一個正整數模數 q:
  定義: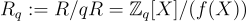
  
  其規範代表是次數小於 n、係數來自 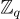的某個規範代表集合的多項式。

• 一個「短」解的實數範數界 β>0，以及樣本數量 m。（像往常一樣，m 往往是次要的，因此不指定它。）
  具體來說，次數 n、模數 q 和範數界 β 可以認為與其在 SIS 問題中的對應物大致相當，而對於環-SIS，m 通常比 SIS 小一個 n 因子（如下所述）。

定義 11.1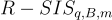

給定 m 個均勻隨機元素 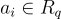，定義一個向量 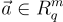，找到一個非零向量 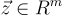，其範數
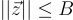，使得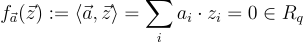

(11.1)

R-SIS 相對於 SIS 的主要優勢是其相對緊湊性和效率: 保證存在足夠短解所需的元素 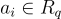的數量 m 僅為 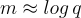，而 SIS 需要 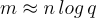。這本質上是因為對於每個 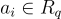，有指數級 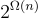個短的環元素 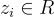可以作為係數使用，而在 SIS 問題中，每個 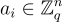只有幾個小的整數係數。此外，使用類似 FFT 的技術，可以在擬線性 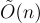時間內計算每個 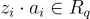，因此對於典型的 q 和 m 選擇，計算 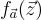的總時間也是擬線性的。

與 SIS 的關係
理解 SIS 和環-SIS 之間形式上的代數相似性和差異是有幫助的。特別是，這種理解提供了將許多密碼學構造從一個問題機械地轉換到另一個問題的方法。這通常也會產生安全性證明的機械轉換，儘管有時需要更顯著的更改。

簡而言之，在環-SIS 中，每個隨機元素 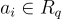對應於 SIS 中的 n 個相關（非獨立）向量 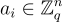，其中 n 是環 R 在 Z 上的次數。類似地，環-SIS 解的每個環元素 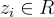代表 SIS 解中的 n 個整數的對應塊。這個經驗法則可以通過將環-SIS 視為具有「結構化」實例的 SIS 的特殊情況來形式化：

• 通過固定 R 的適當 Z-基底，在輸入域 R 和 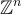之間，以及輸出域 和 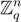之間獲得一個加法群同構，該同構還（至少近似地）保持「短性」。例如，對於 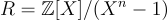，單項式 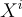對應於第 (i+1) 個標準基底向量 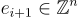（i=0,…,n−1）。這產生了環-SIS 輸入 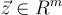與 SIS 輸入 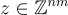之間的對應關係，輸出也類似。

• 乘以任何固定 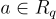的（左）乘法是從 R 到 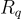的一個 Z-線性函數，因此它可以由一個（結構化的）方陣 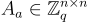表示，該矩陣將 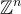映射到 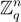。例如，對於 R=Z[X]/(Xn−1)，任何 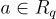對應於其第一列是 a 的係數向量的循環矩陣。這產生了環-SIS 實例 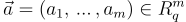與（結構化的）SIS 實例 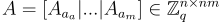之間的對應關係。

用抽象代數的術語來說，在 SIS 中，隨機元素 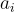從域 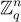中抽取，該域僅被視為一個加法群，即一個Z-模（Z-module）。一個 SIS 解是 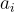的短 Z-組合，其和為零。而在環-SIS 中，隨機元素從 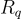中抽取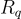， 被視為一個R-模（R-module），而解是一個短的 R-組合，其和為零。更豐富的 R-模結構是效率提升的來源，但也是更專業化的底層最壞情況硬度假設）的來源。