環的幾何
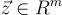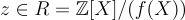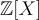環-SIS 實例的解 必須根據 R 上適當選擇的範數足夠「短」。幾項早期工作中使用的範數的樸素選擇由係數嵌入（coefficient embedding）給出，該嵌入將每個 與其在 中規範代表的 n 維整數係數向量相關聯。這個選擇對於發展直覺可能有用，但它不是規範的 — — 它依賴於 RR 的代表的選擇，這些代表不必是次數小於 n 的 X 的多項式 — — 並且它導致對 f(X) 形式的繁瑣約束以及相當粗略的分析。例如，由於模 f(X) 的約化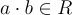，的範數可能僅與 a 和 b 的範數鬆散相關。

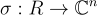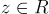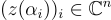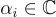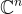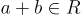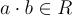一個更好的範數概念由代數數論中的經典概念典範嵌入（canonical embedding） 給出。這個嵌入將每個環元素 映射到向量 ，其中 是 f(X) 的 n 個複根。請注意，z 的任何代表在 中產生相同的向量，這使得嵌入是規範的。它還有一個很好的特性，即和 與積 分別嵌入為 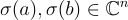的座標方式和座標積，這在加法和乘法下產生了對環元素範數的簡單且相當尖銳的界限。在這強調，典範嵌入和複數主要用於分析，例如在安全性證明中；它們永遠不需要被顯式計算。

理想格與環-SIS 的硬度
簡而言之，與 SIS 類似，可以證明 R-SIS 及其相關的密碼學函數至少與某些最壞情況下的格問題一樣困難。然而，底層的格問題專門針對源於環 R 的代數結構化的格，稱為理想格（ideal lattices）。此外，R 的代數和幾何性質在 R-SIS 可以期望具有哪種安全性質以及底層最壞情況保證的定量強度方面起著主要作用。

理想的格:
簡單來說就是一個對應於 R 中某個理想（ideal）的格，在固定的幾何嵌入選擇下，例如上面描述的係數嵌入或典範嵌入。回想一下，交換環 R 的理想是一個加法子群 I⊆R，它在與 R 的乘法下也是封閉的，即對於每個 v∈I,r∈R，有 v⋅r∈I。這種乘法封閉性意味著理想格具有一般格所不具備的幾何對稱性。例如，在 R=Z[X]/(Xn−1) 的係數嵌入下，一個理想對應於 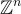中的一個循環格，即該格在 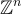座標的循環旋轉下是封閉的。這是因為 R 的理想在乘以 X 下是封閉的，這在係數嵌入中對應於旋轉一個座標。

如下所述，已知的 R-SIS 硬度證明與限制在 R 中理想格上的格問題相關。此類問題的複雜性與任意格略有不同。例如，對於典型的環選擇，對於小的 γ=poly(n) 因子，判定問題 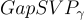在理想格上實際上是容易的，因為代數對稱性強制理想的最小距離位於一個狹窄的、易於計算的範圍內。此外，近似的 SVP 和 SIVP 問題是等價的（有時在近似因子上有小的損失），因為對稱性允許將一個短的非零向量轉換成 n 個相同長度（或接近相同）的線性獨立向量。

對於典型的環選擇，以及密碼學相關的近似因子 γ，理想格上的 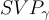和 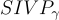問題在最壞情況下似乎非常困難，即使對於量子演算法也是如此。事實上，儘管理想格具有額外的代數結構，相對於相同維度的一般格，目前還沒有已知針對這些問題的顯著加速。特別是，在典型的環選擇中，針對理想格上 SVPpoly(n)​ 的最佳已知（量子）演算法需要指數時間 2Ω(n)。然而，從計算角度來看，理想格的研究還遠不夠深入，因此關於它們的硬度猜想可能還不值得那麼多的信心。

單向性:
對於環 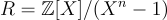和其他適當參數，Micciancio 證明了在方程式 (11.1) 中定義的函數 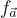是單向的（one-way），假設某些在 n 維循環格（即 RR 中在係數嵌入下的理想格）上的問題在最壞情況下是困難的。等價地，他證明了環-SIS 的非齊次（inhomogeneous）版本的硬度，在該版本中為方程式 (11.1) （對於均勻隨機的右邊項（而非零））尋求一個短解。然而，他留下了一個開放性問題，即確定該函數是否是抗碰撞的（collision-resistant），如同 Ajtai 基於 SIS 的函數一樣。回想一下，抗碰撞性本質上等價於齊次環-SIS 的硬度。

抗碰撞性:
2006 年發表的 Peikert 和 Rosen [PR06] 以及 Lyubashevsky 和 Micciancio [LM06] 的同時且獨立的工作表明，在 R=Z[X]/(Xn−1) 上的函數 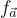結果證明不抗碰撞，即齊次 R-SIS 是容易的。原因在於該環不是一個整環（integral domain），而零因子（zero divisors）可以被用來構造碰撞。

然而，在積極的一面，相同的工作 [PR06, LM06] 表明，在適當的整環 R 上，函數 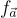確實是抗碰撞的，假設對於 R 中的理想格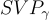， （其中 γ=β⋅poly(n)）在最壞情況下是困難的。合適環的突出例子包括分圓環（cyclotomic rings），例如: 對於 n 是 2 的冪的 Z[X]/(Xn+1)，以及對於質數 p 的 Z[X]/(Xp−1+⋯+X1+1)。通常，分圓環允許非常快速和優雅的環運算，使用 [LMPR08, LPR13] 中詳細描述的類似 FFT 的技術。

來自數域的更緊密近似因子
Peikert 和 Rosen [PR07] 的後續工作推廣了上述結果，證明 R-SIS 至少與 R 中理想格上的最壞情況 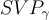一樣困難，其中 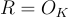是任何數域 KK 中的代數整數環。值得注意的是，在某些數域族中，底層 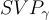問題的近似因子可以小至 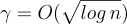。這項工作揭示了數域的判別式（discriminant） — — 本質上是 RR 在典範嵌入下的行列式 — — 如何控制最壞情況的近似因子。

參考資料:
[LPR10] V. Lyubashevsky, C. Peikert, and O. Regev. On ideal lattices and learning with errors over rings. Journal of the ACM, 60(6):43:1–43:35, November 2013. Preliminary version in Eurocrypt 2010.

[PR06] C. Peikert and A. Rosen. Efficient collision-resistant hashing from worst-case assumptions on cyclic lattices. In TCC, pages 145–166. 2006.

[LM06] V. Lyubashevsky and D. Micciancio. Generalized compact knapsacks are collision resistant. In
ICALP (2), pages 144–155. 2006.

[LMPR08] V. Lyubashevsky, D. Micciancio, C. Peikert, and A. Rosen. SWIFFT: A modest proposal for FFT hashing. In FSE, pages 54–72. 2008.

[LPR13] V. Lyubashevsky, C. Peikert, and O. Regev. A toolkit for ring-LWE cryptography. In EUROCRYPT, pages 35–54. 2013.

[PR07] C. Peikert and A. Rosen. Lattices that admit logarithmic worst-case to average-case connection factors. In STOC, pages 478–487. 2007.