在之前的文章也簡單地介紹了 SIS，現在就深入地去講解一下。

短整數解 (SIS) 問題最早出現在阿傑塔 [Ajt96] 的開創性工作中，並作為單向和抗碰撞哈希函數、識別方案、數字簽名和其他“小密碼”原語（但不包括公鑰加密）的基礎。這裡定義 SIS 問題，調查其與最壞情況下格問題的聯繫，並探討其基本屬性和直接的密碼學意義。

定義
非正式地，SIS 問題要求，給定某個大有限加法群的許多均勻隨機元素，找到一個足夠“短”的非平凡整數組合，使其和為零。更正式地，SIS 由正整數 n 和 q 定義群 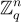，正實數 β，以及群元素的數量 m 參數化。（參數 m 是次要的，因此有時不指定它。）具體來說，可以將 n 視為主要的硬度參數（例如 n≥100），而 q>β 至少是 n 的小多項式。

短整數解 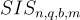的定義
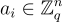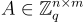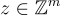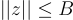給定 m 個均勻隨機向量 ，形成矩陣 A 的列，找到一個非零整數向量 ，其範數 ，使得:

。

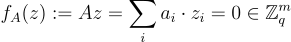現在強調關於 SIS 問題的幾個簡單但有用的觀察：

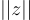• 沒有對 的約束，可以通過高斯消元輕鬆找到解。類似地，必須取 β<q，否則 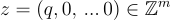將始終是一個合法的解。
• 對於矩陣 A 的任何解，可以通過在解向量後附加零（這不改變解的範數）輕鬆轉換為任何擴展 的解。換句話說，可以根據需要忽略列 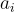，因此隨著 m 的增加，SIS 問題只能變得更簡單。類似地，隨著 n 的增加，它只能變得更難。
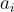• 範數界 β 和向量 的數量 m 必須足夠大以保證解的存在。當 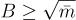且 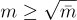時就是這種情況，其中 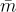是大於 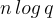的最小整數，通過鴿巢原理：首先，根據前面的觀察，可以不失一般性地假設 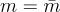。然後因為有超過 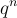個向量 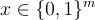，所以必須有兩個不同的 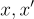使得 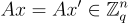，因此它們的差 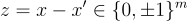是一個範數最多為 β 的解。
• 上述鴿巢論證實際上表明更多：誘導的函數族
  
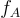  是抗碰撞的，假設相應 SIS 問題的難解性。這是因為 的碰撞 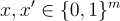立即產生 A 的一個 SIS 解。（當然，域 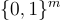在這裡有些隨意，可以用任何其他足夠大的足夠短整數向量集代替。）
  SIS 問題可以看作是某類 mm 維整數格上的平均情況短向量問題，
  即所謂的“q-ary”格：

借用編碼理論的術語，這裡 A 充當“奇偶校驗”（或更準確地說，“arity-check”）矩陣，定義了格 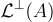。SIS 問題要求在 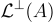中找到一個足夠短的非零向量，其中 A 是均勻隨機選擇的。

還可以考慮 SIS 問題的非齊次版本，即對於均勻隨機且獨立的 A,u，找到 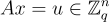的短整數解。注意，忽略範數約束，所有解的集合是格陪集 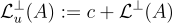，其中 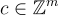是任意（不一定短）的解。可以證明，對於典型參數，齊次和非齊次問題基本上是等價的。

正規形式
SIS 問題允許一個小而重要的優化，稱為（埃爾米特）“正規形式”（HNF），它將實例 A 的大小壓縮了 n 列，而不影響密碼功能或硬度。其工作原理如下：首先，可以假設 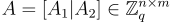的最左邊 n 列 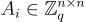在 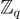上形成可逆矩陣，這是不失一般性的，因為如上所述，可以根據需要忽略列。然後將 A 替換為

，

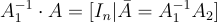並將 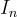子矩陣視為隱含的。注意 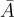是均勻隨機的，因為 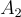是均勻且獨立於 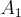的。此外，A 和 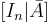具有完全相同的（短）SIS 解。因此，後者形式的 SIS 實例至少與前者類型的實例一樣難解。

硬度

從阿傑塔的開創性工作 [Ajt96] 開始，一系列工作已經建立了關於 SIS 問題相對於最壞情況下格問題硬度的逐步更強的結果。所有這些結果都是以下模板的實例：

定理1
對於任何 m=poly(n)，任何 B>0，以及任何足夠大的 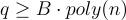，以不可忽略的概率解決 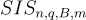至少與在最壞情況下解決任意 n 維格上的決策近似最短向量問題 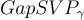和近似最短獨立向量問題 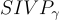（以及其他）一樣困難，對於某些 。

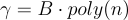請注意，m 和 q 的精確值（除了其下界）在最終的硬度保證中基本上不起作用，但近似因子 γ 隨著 SIS 解的範數界 β 的增加而降低。該定理通過給出一個多項式時間歸約來證明，該歸約使用 SIS 的預言機（在平均情況下以顯著概率工作）來解決任意 n 維格上的 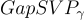和 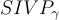。這種歸約的核心挑戰在於生成一個均勻隨機的 SIS 實例，其解以某種方式有助於找到任意格的短向量；下面對此進行高層次描述。

在阿傑塔的原始工作中，與模數 q 和近似因子 γ 相關的 poly(n) 因子是相當大的多項式。從那時起，幾項工作已經顯著改進了這些因子，從而產生更小的實例（例如密碼密鑰）和更強的硬度保證。一些最顯著的改進如下：

• Micciancio 和 Regev [MR04] 的 2004 年工作獲得了 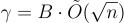的近似因子，對於 β 的有意義選擇，可以小至 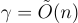，模數 q 可以小至 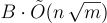。這項工作使用格上的高斯分佈，並建立在 [Ban93, Reg03, AR04] 首次開發的調和分析技術之上。特別是，它定義並分析了格平滑參數 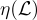的重要概念（已經隱含在 [Ban93, Reg03] 中），這是“平滑掉”格的離散結構所需的高斯“模糊”量。這種平滑使得歸約能夠生成與任意輸入格有意義鏈接的均勻隨機 SIS 實例。

• Gentry、Peikert 和 Vaikuntanathan 的 2008 年工作 將 q 的界限改進到小至 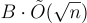，同時保持 [MR04] 中的 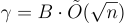近似因子。主要的新成分是一個技術上更簡單的歸約，完全使用格上的離散高斯分佈，避免了與連續高斯相關的“舍入”誤差。為此，歸約使用了 GPV 的離散高斯採樣算法，如下面的定理 5.4.2 所述。

• Micciancio 和 Peikert [MP13] 的 2013 年工作進一步將 q 的界限改進到小至 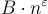，對於任何常數 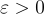。回想一下，這個界限基本上是最優的（除了 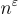因子），因為任何 SIS 實例都有範數 q 的平凡解。歸約獲得的近似因子 γ 有些微妙，因為它可以取決於 SIS 解的 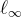範數，而不是通常的 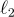範數。這是由於歸約使用 SIS 預言機通過幾個其他離散高斯的組合產生一個離散高斯，使用類似於 [Pei10] 中證明的“卷積引理”。

歸約概述:

證明定理 4.1.2 的所有最壞情況/平均情況歸約都遵循以下模板，最初由 Ajtai [Ajt96] 提出。回想一下，歸約被給予一個任意 n 維格 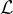的基底 B，以及一個平均情況的 SIS 預言機（oracle），其目標是為某個 γ=poly(n) 求解 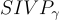，即找到 n 個線性獨立的格向量，其長度均不超過 。

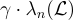在最高層次上，歸約使用一組線性獨立的格向量 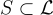（從輸入基底 B 開始），連同其 SIS 預言機，來獲得一個新的集合 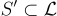，使得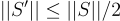
，其中對於集合 ，
。
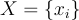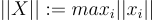然後它反覆重複這個過程，直到停止工作，此時可以保證最終的集合確實是 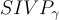的解。

為了實現上述策略，歸約使用以下「核心步驟」:

1. 使用當前的格向量集合 S，生成 m 個「分佈良好」且儘可能短的隨機格向量 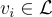。² 讓這些向量形成矩陣 V 的列。

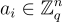2. 定義 為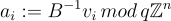
   ，
   即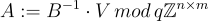
   ，
   並將此實例給予 SIS 預言機。（注意，因為 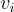是格向量，所以 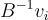是整數。）

3. 如果預言機返回一個有效的解 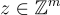，則輸出 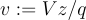. 通過足夠多次重複這個核心步驟，歸約可以獲得許多向量 v，（其中一部分）將組成下一個集合 S′。為了使這一切按預期工作，需要證明以下幾點:

• 如果 z 是 A 的 SIS 解，則 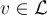且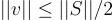
  。
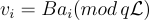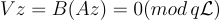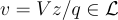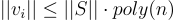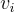  第一個主張由構造得出: 因為 ，所以會有 , 所以 。對於第二個主張，可以生成滿足 的向量 。那麼因為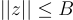
  ， 因此有。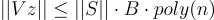
  因此，對於足夠大的 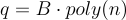，可以確保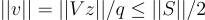
  。

• SIS 實例 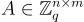是（近乎）均勻的。 因為 SIS 預言機僅被假設在均勻隨機實例上有效（以顯著機率），需要證明由歸約構造的實例是這種情況（達到可忽略的統計誤差）。如果
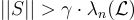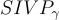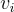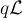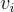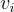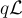  — 即如果還沒有 解 — — 那麼這成立，本質上是因為 模 是足夠「分佈良好」的。更具體地說，對於 的適當分佈，可以使用平滑參數（參見第 2.3 節）來證明 mod 在 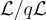上近乎均勻，因為 。
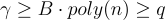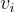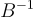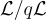  實際上，在這裡並不需要 q 的上界：如果 q>γ，可以從一個寬度為 q/γ 倍的更寬分佈中取樣 ；當最後除以 q 時，這種效應會被完全抵消。最後，因為乘以 是從 到 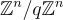的雙射，所以每個 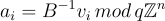也是近乎均勻的。

• 向量 v 的某個子集是滿秩的（即 v 不全位於 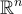的某個真子空間中）。 最後，必須證明即使是惡意的 SIS 預言機也不能，例如，強迫所有向量 v 為零。這再次源於 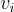是「分佈良好」的事實，但方式略有不同。具體來說，在給定任何固定的 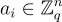值的條件下，真實的 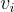；在陪集 - 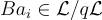上是均勻分佈的。因此，在給定任何固定的 SIS 實例 A 和解 z 的條件下，隨機變量 Vz 仍然是足夠分佈良好的，使得 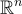的任何真子空間都缺乏其顯著部分的機率質量，因此通過獲得足夠多的向量 v，可以得到一個 full-rank 集合