前情提要

昨天主要是複習這兩周學習過的觀念，也說明了為什麼需要位置編碼，因為 attention 具有位置不變性。

參考文章:
https://www.cnblogs.com/rossiXYZ/p/18744797
https://zhuanlan.zhihu.com/p/454482273
https://huggingface.co/blog/designing-positional-encoding → 可以搭配動態圖一起學習

位置編碼分成兩種，但以下都簡稱位置編碼 PE

1. (learned) position embedding → 透過模型學習而來如 bert
2. position encoding → 規則直接計算

1.位置編碼演進

以下整理成表格方便比對。
核心觀念: 自然數 → 等差數列 → 二進制 → 三角函數

(補充一)
ex 1:
"The cat chased the mouse."
→ token 列表：[The, cat, chased, the, mouse]
→ 語義結構: 主語 + 動詞 + 受詞
→ [0.00, 0.25, 0.50, 0.75, 1.00]

"The small orange cat quickly chased the frightened mouse."
→ token 列表： [The, small, orange, cat, quickly, chased, the, frightened, mouse]
→ 語義結構: 仍然是 主詞 + 動詞 + 受詞，只是在修飾詞和副詞上更複雜
→ [0.00, 0.125, 0.25, 0.375, 0.50, 0.625, 0.75, 0.875, 1.00]

上面同樣是"主詞/動詞/受詞"，但它們的相對位置不一致
在句子 A 中， chased 在序列中為 0.5，而在句子 B 中，它在 0.625。
ex 2:

當中北國這個詞是相鄰的，照理說不管序列的長度多少，相同位置的 token 之間的相對位置應該保持一致。

(補充二)

用我們數位邏輯當中的二進制的方式來表達位置編碼，然後位置編碼可以直接與詞向量做相加，但是離散的如下圖。
(電腦採用二進制也就是只有 0, 1，我們生活是用十進制也就是 0 ~ 9)

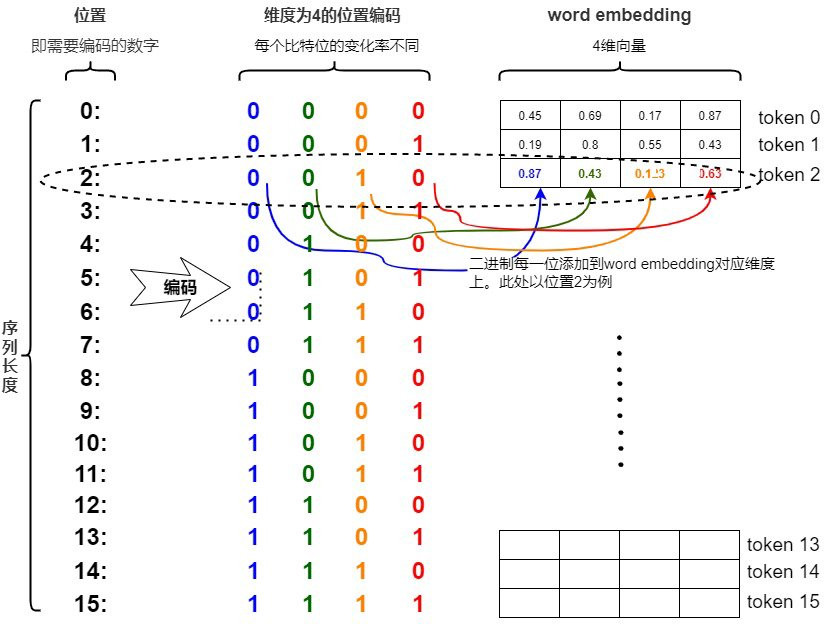
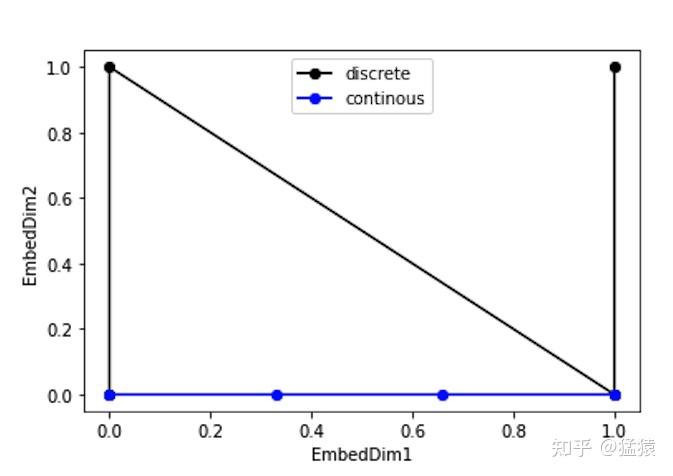
到這邊先稍微總結一下，上面已經解決數值範圍的問題，不同的序列長度保持一致的唯一編碼。但一樣有以下問題:

1. 上面都是整數，但詞向量那些都是浮點數
2. 上述基本上都是單調函數方法(後續 token 的位置編碼 > 前面 token 的位置編碼)，追求"絕對位置"

我們希望建構重心在相對位置，舉個例如，如果模型學會了「貓」和「可愛」之間有某種特定的關係，這個關係應該與它們在句子中的絕對位置無關。也就是說，不論是「那隻貓很可愛」還是「這是一隻很可愛的貓」，模型都能捕捉到這兩個詞之間的相對距離和關係。
所以希望透過一個 function 來取得相對位置，相對位置信息=f(絕對位置信息)。
目標滿足以下幾點:

• 值的範圍有界
• 平滑, 連續
• 可以表達相對位置的函數

2. 三角函數編碼

核心觀念: 透過 sin 和 cos 函數的線性變化 → 提供位置資訊
sin 跟 cos 相信大家都不陌生，是一個週期為 2pi 的週期函數，並且值域為 [-1, 1]，以上就滿足有界跟平滑連續了，那相對位置可以透過兩角和差公式，如以下公式及說明。
  
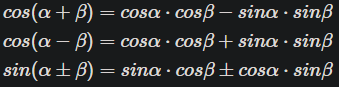
說明: 任意兩個位置 p1 和 p2 之間的相對位置關係可以透過簡單的線性變換來表示。舉例來說，sin(θ+Δθ) = sin(θ)cos(Δθ) + cos(θ)sin(Δθ)。這使得模型可以輕鬆地學習並應用於相對位置的模式，而不受絕對位置的影響。

這裡我們更進一步整理為矩陣的樣子，其中 T_Δt 為二維向量空間當中的旋轉矩陣:

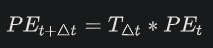
所以在 Transformer 原始論文提出來的絕對位置編碼方案如下
  
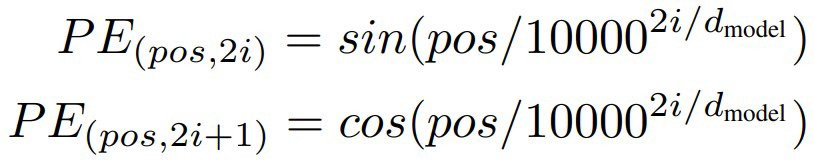
那我們可以再透過下圖了解到，假設 embedding 只有6維，那我們兩兩一組，偶數的地方為 sin，奇數的地方為 cos。

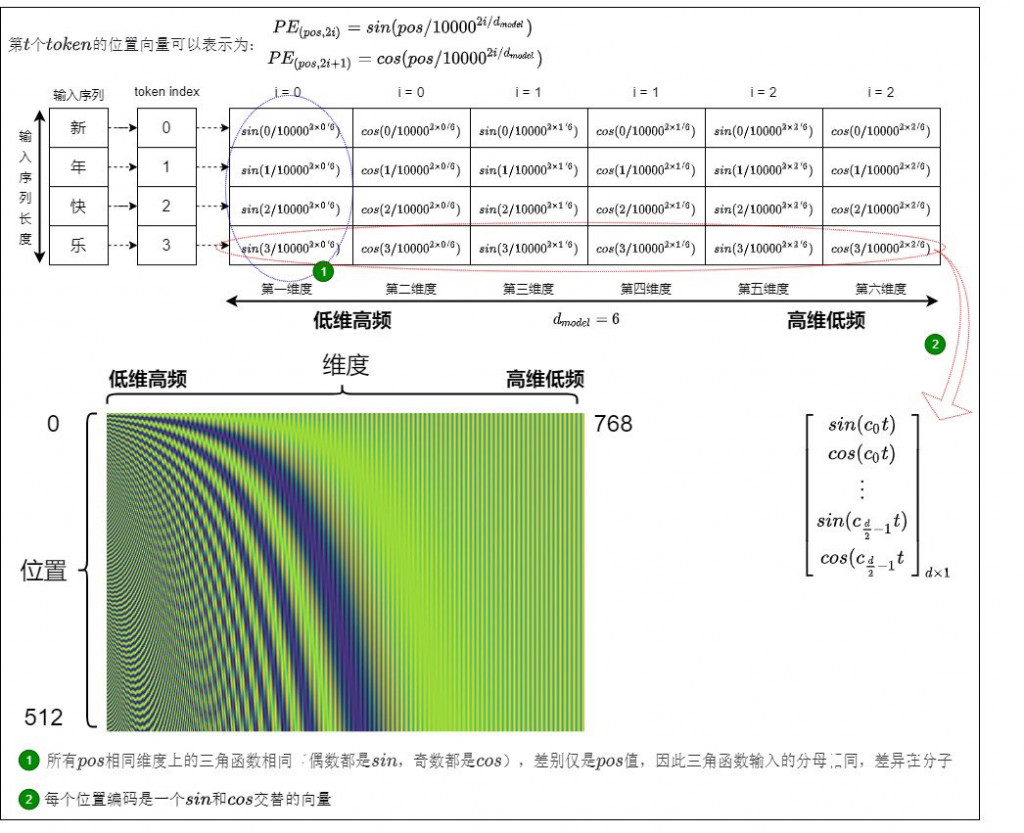
假設我要用 token index 1 找到 token index 3 的相對位置，我就可以透過剛才的公式，將數值帶入，就可以找到了，其中 ci 為 10000^(2i/d_model)

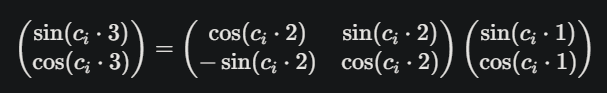
最後讓我們從另外一個角度來看，三角函數式位置編碼其實就是以旋轉的方式給詞向量注入位置資訊。如果我們是用加法將詞向量和位置向量合在一起，也相當於是在原始的詞向量上施加一個平移。

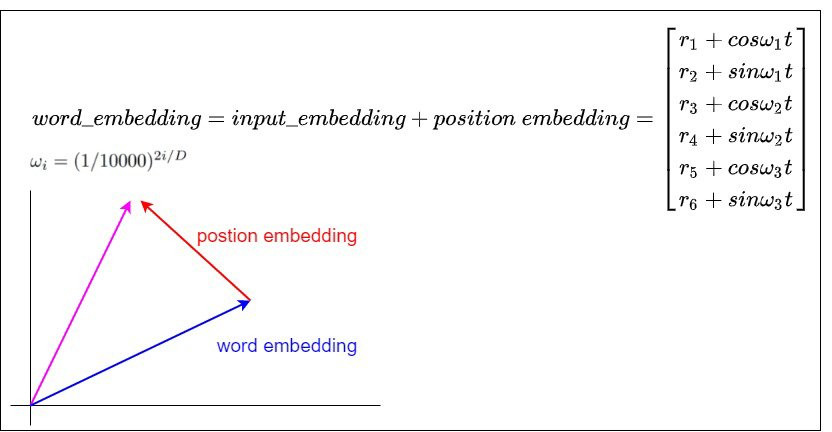
明天再更詳細介紹跟實作，今天就先到這裡囉~