Hoffstein, Pipher, 和 Silverman [HPS98] 的 NTRU 密碼系統是早期的基於格的密碼學提案。幾個計算問題自然地與 NTRU 系統相關。

定義 14.1 (NTRU 學習問題):
對於可逆的 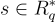和 R 上的一個分佈 χ，定義 為輸出 ， 其中 e←χ 的分佈。
NTRU 學習問題是：給定獨立樣本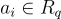

其中每個樣本根據以下之一分佈:
(1) 對於某個隨機選擇的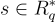
（對所有樣本固定）的

或

(2) 均勻分佈，區分是哪種情況（以不可忽略的優勢）。

在 NTRU 密碼系統中，公鑰是一個對於短的 s 的樣本 e/s，而密文本質上對應於具有相同分母 s 的額外樣本，儘管分子可能不那麼短。

正如環-LWE 的標準形式一樣，我們可以在不失一般性的情況下假設秘密分母 s 是從分佈 χ 中選擇的，限制在 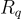中的單位元（units）上。這是因為給定來自某個任意 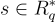的
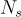的樣本 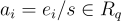，我們可以取一個是單位元的樣本，稱之為 ，並將剩餘的樣本除以它，得到樣本 其公共分母是短的單位元

因為對均勻隨機樣本進行相同的變換會保持均勻分佈，所以能夠區分標準形式的 NTRU 樣本與均勻樣本，就意味著能夠對具有任意分母的 NTRU 樣本進行區分。

NTRU 和環-LWE 問題在語法上非常相似，甚至可以視為同一問題的齊次和非齊次版本。具體來說，對於 NTRU 樣本 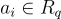，存在一個秘密 s，使得每個 對於某個短的 而對於環-LWE 樣本 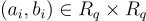存在一個秘密 s，使得每個 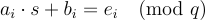對於某個短的 。
這種解釋通常使得將密碼學構造從一個問題改編到另一個問題成為可能。

環-LWE 至少與 NTRU 一樣難
這裡簡要地概述一個證明，說明對於適當的參數，環-LWE 至少與 NTRU 學習問題一樣難。儘管證明策略現在相對標準，但尚未看到這個特定結果被記錄過。更具體地說，描述一個從 NTRU 的判定版本到環-LWE 的搜尋版本的歸約。使用後者問題的搜尋-判定等價性，也可以將歸約擴展到判定版本，但有一個需要注意的地方，將在下面解釋。歸約通過一個「有損性」（lossiness）論證來工作，à la [PW08, Pei09, DM13, MP13]。假設有一個預言機 O，給定 ℓ 個樣本，能以高機率求解搜尋-R-LWE。那麼一個求解 NTRU 學習問題的演算法如下工作：給定 ℓ 個樣本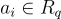

作為輸入，它從 LWE 誤差分佈 χ 中選擇一個秘密 s 和誤差

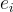並將對

給予O，O 返回某個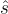

如果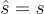

演算法會接受（accept），否則拒絕（reject）。

為了分析這個歸約，首先考慮

是均勻隨機的情況。那麼我們提供給 O 的輸入由具有秘密 s 的正確分佈的環-LWE 樣本組成，所以 O 必須以高機率返回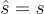

因此演算法會接受。在另一種情況下，有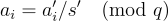

對於從 NTRU 問題中使用的分佈 χ′ 中抽取的某個隨機短的

那麼只要 LWE 誤差分佈 χ 比 χ′ 足夠「寬」，對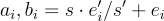

就資訊理論上隱藏了 s 的值。也就是說，存在多種可能性的秘密和誤差與這些對一致；例如，它們可以分別是短元素 s+s′ 和 ei​−1。因此，無論預言機 O 內部如何工作，即使其輸入對不是正確分佈的環-LWE 樣本，它也不能可靠地猜測我們的演算法選擇的特定 s，因此演算法以顯著的機率拒絕。這意味著演算法在區分 NTRU 樣本和均勻隨機樣本方面具有顯著的優勢，如期望的那樣。

當然，上述概述省略了有損性論證所需的精確計算，但這些計算現在是相當常規的。因此注意到為了使有損性成立，χ 和 χ′ 的寬度之比必須隨著 ℓ（預言機 O 用於搜尋-環-LWE 的環-LWE 樣本數量）增長而增長。如果我們希望通過環-LWE 的已知搜尋-判定等價性來連接 NTRU 和環-LWE 的判定版本，那麼 ℓ 可以是一個無界多項式（它與環-LWE 區分器的優勢成反比）。因此，χ 和 χ′ 的寬度之比將需要是超多項式的，這削弱了結果。一個可能規避這個問題的方法是給出環-LWE 的一個保持樣本數量（sample-preserving）的搜尋-判定等價性。

參考資料
[HPS98] J. Hoffstein, J. Pipher, and J. H. Silverman. NTRU: A ring-based public key cryptosystem. In ANTS, pages 267–288. 1998.