在 2010 年發表的工作中，Lyubashevsky, Peikert, 和 Regev [LPR10] 引入了環-LWE，這是誤差學習的基於環的類比，並證明了下面描述的硬度定理。（Stehlé 等人 [SSTX09]) 的一項同時且獨立的工作也考慮了對於形式為 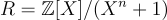（n 是 2 的冪）的環的環-LWE 特殊情況，並證明了較弱的結果，例如，它缺少對判定形式的硬度證明）。
在處理環-LWE之前，需徹底理解與環-SIS相關的定義和問題。

定義
環-LWE 由一個在 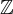上度為 n 的環 R、一個定義商環 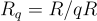的正整數模數 q，以及一個在 R 上的誤差分佈 χ 來參數化。通常，取 R 為一個分圓環，而 χ 是在 R 的典範嵌入下的某種離散化高斯分佈，可以粗略地認為其相對於 q 具有「誤差率」 。

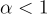定義 13.1 (環-LWE 分佈)
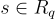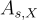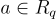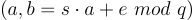對於稱為秘密的 ，在 上的環-LWE 分佈 是通過均勻隨機選擇 ，選擇 ，並輸出 來取樣。

注意到，在 [LPR10] 的環-LWE 分佈的原始定義中，秘密 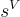和有噪聲的乘積 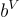實際上屬於 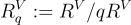，其中 R∨ 是與 R 對偶的某個分式理想（fractional ideal）。事實證明，當在 R 的典範嵌入中使用（近）球形誤差（(near-)spherical errors) 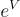時，這是硬度證明和密碼學應用的正確定義，這種誤差最容易分析和推導尖銳的界限（詳見 [LPR10, Section 3.3] 和 [LPR13]）。上面定義的問題的形式（其中 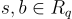) 可以簡單地通過將 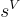和 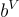乘以某個「調整」（tweak）因子 t（其中 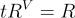）從剛才描述的版本獲得：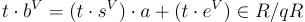

注意，這產生了誤差 e 的一個「調整過的」、可能非球形的分佈 χ。然而，這兩種問題形式在計算、應用、分析等方面是完全等價的，因為調整是可逆的。（在 [DD12] 中描述了用 R 替換 R∨ 的另一種方法，但它會招致一些計算和分析上的損失，因為它不是可逆的。）

R-LWE 問題的判定版本是區分環-LWE 樣本和均勻隨機樣本。像往常一樣，也用可用樣本的數量 m 來參數化這個問題，有時不指定它。

定義 13.2 (判定-RR- )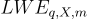
給定 m 個獨立樣本 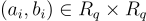，其中每個樣本根據以下之一分佈：(1) 對於均勻隨機的 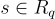（對所有樣本固定）的 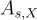，或 (2) 均勻分佈，區分是哪種情況（以不可忽略的優勢）。

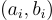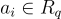與 LWE 一樣，沒有誤差時環-LWE 問題是容易的，因為在情況 (1) 中，如果給定一個樣本 且 是可逆的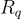（ 的大多數元素都是），有 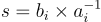，而在情況 (2) 中，幾乎永遠不存在一個單一的 s 與所有樣本一致。類似地，環-LWE 有一個標準形式（normal form），其中秘密 s 是從誤差分佈（模 q）中選擇的，而不是均勻的。

環-LWE 的主要優勢是其緊湊性和效率：每個樣本 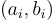產生一個 n 維的偽隨機環元素 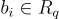，而不是像在 LWE 中那樣只產生一個單一的偽隨機純量 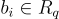。此外，使用類似 FFT 的技術，環乘法可以在僅擬線性 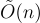時間內執行，因此可以在每個僅 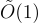攤銷時間內生成這些 n 個偽隨機純量。例如，這一切都產生了一個公鑰加密方案，其在加密/解密時間和密文空間上僅有 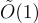因子的開銷，相對於明文傳送。

與 LWE 的關係
理解 LWE 和環-LWE 之間的代數相似性和差異是有幫助的。正如（環）SIS 一樣，一個具有隨機 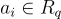的單個環-LWE 樣本取代了具有隨機 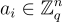的 n 個 LWE 樣本。因此，環-LWE 可以被視為具有「結構化」（相關）樣本的 LWE 的特殊情況。

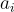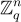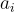用抽象代數術語來說，在 LWE 中，秘密 s 和隨機 是 的元素，被視為一個 Z-模，並且它們使用Z-雙線性內積 相乘。相比之下，在環-LWE 中，秘密 s 和隨機 是 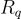的元素，被視為一個 R-模，並且它們使用 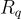中的標準R-雙線性乘法相乘。

硬度
與 LWE 類似，環-LWE 享有最壞情況硬度保證，這裡非正式地陳述如下：定理 13.3 ([LPR10])。 對於任何 m=poly(n)，度為 n（在 Z 上）的分圓環 R，以及模數 q 和誤差率 α<1 的誤差分佈 χ 的適當選擇，求解 R-LWE q,χ,m​ 問題至少與量子求解在 R 中任意理想格上的 SVPγ​ 問題一樣困難，其中某個 γ=poly(n)/α。

請注意，與 LWE 一樣，近似因子 γ 隨 χ 的誤差率 α 的倒數變化。然而，與 LWE 不同的是，因子 γ 也隨著樣本數量 m 的增加而輕微變差。這種變差可能是證明技術的一個假象，無論如何，它可以通過從某個族中隨機選擇誤差分佈本身來避免。詳見 [LPR10] 的主要定理。

如上所述，在上述定理中，誤差分佈 χ 的精確形式有些微妙，因為它依賴於典範嵌入以及將 R∨R∨ 轉換為 RR 的「調整」因子（當使用定義 4.4.1 中的問題形式時）。特別是，誤差項 e←χ 的 Z-係數在 R 的任何 Z-基底中不一定是獨立的，但在適當的基底選擇下仍然可以非常高效地取樣。完整細節見 [LPR10, LPR13]。

上述定理分兩部分證明：首先，使用量子歸約證明環-LWE 的搜尋版本（即從 As,χ​ 給定許多樣本恢復秘密 s）至少與 SVPγ​ 一樣困難。證明的這部分實際上適用於數域的任何代數整數環 R（不僅僅是分圓環）和任何足夠大的模數 q。然後，使用一個經典的搜尋到判定歸約（search-to-decision reduction）來證明判定版本至少與搜尋版本一樣困難。證明的這部分依賴於分圓環和模數 q 的形式的額外代數性質，即分圓環在有理數上是伽羅瓦（Galois）的，並且 q 在 R 中分裂為不同小範數素理想的乘積。

推廣
Brakerski, Gentry, 和 Vaikuntanathan [BGV12] 引入了廣義環-LWE 問題 (RR-GLWE)，它本質上在 LWE 和環-LWE 之間插值：秘密是一個環元素的向量 s∈Rqk​，而 GLWE 樣本的形式為(a,b)∈Rqk​×Rq​，其中要麼 b=⟨s,a⟩+emodq（對於 e←χ)，要麼 b∈Rq​ 是均勻隨機的。對於 R=Z，這特化為 kk 維 LWE k,q,χ​ 問題，而對於 k=1，它特化為 R-LWE q,χ​。推廣定理 13.3，Langlois 和 Stehlé [LS15] 證明了 R-GLWE 至少與量子近似求解所謂模格（module lattices）上的最壞情況格問題一樣困難，模格是對應於 R-模 M⊆Rk 的格

參考資料:
[LPR10] V. Lyubashevsky, C. Peikert, and O. Regev. On ideal lattices and learning with errors over rings. Journal of the ACM, 60(6):43:1–43:35, November 2013. Preliminary version in Eurocrypt 2010.