基本密碼學構造
在本章中，會詳細講述一系列基於（環-）SIS/LWE 問題的格密碼學核心構造。介紹按密碼學物件類型組織，接下來會以多篇文章進行深入講解。

15.1 抗碰撞雜湊(Hash)函數
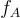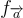在上幾篇的章節提及，函數 和 分別在第8篇和11篇中提及到相關定義，在假設對應的（環-）SIS 問題難解的前提下是抗碰撞的。

Lyubashevsky 等人 [LMPR08] 定義了 SWIFFT，它是基於環-SIS 的雜湊函數 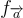的一個具體實例化。選擇該實例化是為了允許使用各種 FFT 和預計算技術進行快速計算，並具有針對已知密碼分析攻擊估計 2^(100) 安全等級的抗碰撞性。應注意 SWIFFT 的參數化對應於一個空洞的最壞情況安全保證，因為環的次數 n=64 足夠小，可以在適度的時間內在 n 維格中找到相對短的向量。然而，這並不意味著 SWIFFT 不安全，因為最壞情況保證僅提供了破壞函數難度的下界。實際上，Ajtai 函數的 SWIFFT 及其他實例化似乎比硬度證明中使用的最壞情況問題要難破解得多。

15.2 被動安全加密
自從（環-）LWE 問題被引入以來，大量加密方案和其他應用都基於它們。在本小節中，給出基於 LWE 的、具有被動（IND-CPA）安全性的公鑰加密方案的半時間線。在非正式地，看到公鑰和加密消息的被動竊聽者無法得知這些消息的內容。本節介紹的許多方案具有額外的有用特性（例如: 同態性、對金鑰相關消息的安全性），在討論中大多省略這些特性。

15.2.1 Regev 的 LWE 密碼系統
回想 Regev [Reg05] 給出了第一個基於 LWE 的公鑰加密方案，其中公鑰為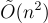
位元，私鑰和密文為 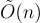位元，且每個密文加密單一位元。在這裡的 n 是底層 LWE 問題的維度。在多用戶設定中，如果存在一個可以在所有用戶之間共享的可信隨機源，則每個用戶的公鑰大小可以減少到只有 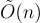位元。

系統描述:
該密碼系統由 LWE 維度 n、模數 q、Z 上的誤差分佈 χ 以及樣本數量 m 參數化，所有這些參數應滿足安全和正確解密所需的各種條件，如下所述。

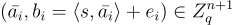• 私鑰 是一個均勻隨機的 LWE 秘密 ，而公鑰是從 LWE 分佈 抽取的一些 m≈(n+1)logq 個樣本 ，收集為矩陣的列
  
  此公式為 (15.2.1)
  其中 在多用戶設定中， 可以由可信方選擇並在所有用戶之間共享，用戶的公鑰僅為 b。請注意，根據定義，私鑰和公鑰滿足關係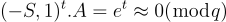
  
  此公式為 (15.2.2)

• 要使用公鑰 A 加密一個位元 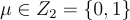， 只需取 LWE 樣本的隨機子集和，並在最後一個座標中適當編碼消息位元。具體地說，選擇一個均勻隨機 並輸出密文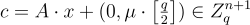
  
  此公式為 (15.2.3)
  請注意忽略 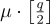加密僅僅是第8篇中的函數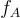

在隨機二進位輸入 x 上的求值，儘管這裡矩陣 A 不是均勻隨機的，而是偽隨機的。 從 [KTX08, PW08] 觀察到，只要 q/p 足夠大，可以使用 q/p 代替 q/2 來加密來自 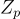的消息。

• 要使用私鑰 s 解密，計算
  
  
  
  此公式為 (方程式 (5.2.2))
  
  是短的並測試其模 q 後更接近 0 還是

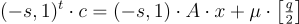
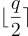
請注意，只要累積誤差 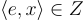的幅度小於 q/4，解密就是正確的。這可以通過選擇相對於誤差分佈 χ 和 m 的值足夠大的 q 來實現。例如，如果 是離散高斯分佈，其參數為 r 的次高斯分佈，那麼 是參數至多為 的次高斯分佈，因此以至少 的機率其幅度小於 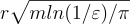為了確保以壓倒性機率正確解密，同時在最壞情況假設下保持安全性（如下所述），可以使用小至 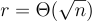和 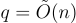的參數，這對應於 LWE 誤差率 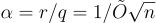和最壞情況近似因子 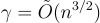使用稍大的模數 q，甚至可以在金鑰生成期間拒絕任何（可忽略地罕見的）歐幾里得範數過長的誤差向量 e，從而確定地確保正確解密。

安全性:
Regev 的系統在語義上對抗被動竊聽者是安全的，前提是判定-LWEn,q,χ,m​ 是難解的，這對於適當的參數，可由假設的格問題最壞情況（量子）硬度所蘊含。

這裡給出安全性證明的相當詳細的概述，它遵循一種後來被稱為「有損性」(lossiness) 論證的策略。

兩個主要思想是:

1. 正確形成的公鑰 A 與「畸形」的均勻隨機公鑰是不可區分的；
2. 在此類畸形金鑰下加密是資訊理論上安全的。更正式地說，希望證明對於固定位元 μ，公鑰 A 連同其加密的密文 c 對於 μ=0,1 是不可區分的（參見第 2.4.2 節）。通過考慮一系列產生 A,c 的替代或「混合」(hybrid) 實驗來進行:

在第一個混合實驗中，公鑰 A 是「畸形」的，因為它是從
中均勻隨機選擇的，而不是從 LWE 樣本生成的。（請注意，沒有對應的私鑰。）密文 c 是通過使用 A 以通常方式加密 μ 生成的，即 。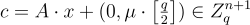

聲稱在 LWE 假設下，這個實驗與真實實驗是不可區分的。這通過一個歸約來證明：任何旨在區分兩個實驗的假想攻擊者 A 都可以轉換為旨在區分 LWE 樣本與均勻隨機樣本的演算法 D，即它攻擊判定-LWE n,q,χ,m​: D 簡單地將其輸入樣本收集到矩陣 A 中，使用 A 加密 μ 得到密文 c，並在 (A,c) 上調用 A，輸出相同的接受/拒絕決定。顯然，D 完美地模擬了真實或混合實驗，這取決於其輸入樣本是 LWE 還是均勻的（分別）；因此，D 和 A 具有相同的區分優勢。因為根據假設，D 的優勢必須是可忽略的，所以 A 的優勢也是。

在第二個混合實驗中，公鑰 A 仍然是均勻隨機的，但現在密文
也是均勻選擇的，並且獨立於 A。聲稱這個實驗與前一個實驗在統計上是不可區分的，即即使是計算無界的攻擊者也只有可忽略的優勢來區分它們。換句話說，在均勻隨機公鑰下加密是「有損的」，因為它在資訊理論上隱藏了消息。該主張直接源於

足夠大這一事實，以及一個正則性引理，也稱為剩餘雜湊引理 [HILL99]，該引理表明，對於均勻且獨立的 和 ，(A,u=A⋅x) 在統計上與均勻隨機是不可區分的。將任何固定向量 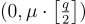加到 u 上保持了其均勻分佈。

總之，因為上述實驗對於任何固定位元 μ 是不可區分的，並且最後一個實驗完全與 μ 無關，所以對於 μ=0,1 的兩個真實實驗也是不可區分的。

作為最後的評論，注意到該系統在主動或選擇密文攻擊下是容易被攻破的。

標準形式優化:
如 [MR09] 所記錄，上述密碼系統，以及基本上所有其他基於 LWE 的系統，都可以使用之前定義的 SIS/LWE 的 "標準形式" 進行輕微優化。實際上，下面描述的一些系統明確地包含了這種優化。對於與上面相同的參數 n,m，讓矩陣 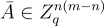只有 m−n 列，並如 Regev’s LWE Cryptosystem 定義
其中 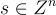的座標是從誤差分佈χ 中選擇的。要加密一個位元

選擇一個均勻隨機的 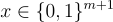並輸出密文

給定私鑰 s，解密時計算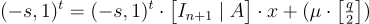



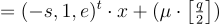
(方程式 (15.2.2))
(s, e, x 是短的) 並測試其模 q 後更接近 0 還是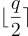

該變體的安全性證明與上面概述的證明基本相同，但現在它依賴於判定-LWE 標準形式的硬度，以及對於均勻隨機 A 的形式為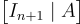 的矩陣的正則性引理。

更長的消息
通常，大家都希望一次加密多個位元，例如: 傳輸對稱加密方案的密鑰。在這種情況下，Peikert、Vaikuntanathan 和 Waters [PVW08] 描述了一種使用攤銷(amortization) 技術的顯著效率改進。在他們的變體中，每個密文可以加密 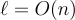個位元，而公鑰或密文的大小沒有漸近增加，加密的執行時間也沒有增加。然而，私鑰大小和解密運行時間增加到
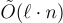而原始系統中為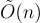
主要思想是，不使用形式為 的 (n+1)行的公鑰，而是生成形式為

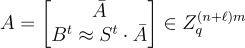
的 (n+ℓ) 行金鑰，其中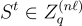

的 ℓ 行是獨立的 LWE 秘密，並且

的每個條目都被從 χ 抽取的獨立誤差擾動。加密消息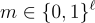

的工作原理基本與之前相同，選擇均勻隨機的

並輸出密文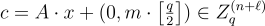

對於安全性，通過常規的混合論證，可以證明在判定-LWE 的硬度假設下，公鑰 A 與均勻分佈是不可區分的。此外，對於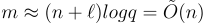

上面描述的正則性引理和有損性論證仍然適用，從而確立了語義安全性。

參考資料
[LMPR08] V. Lyubashevsky, D. Micciancio, C. Peikert, and A. Rosen. SWIFFT: A modest proposal for FFT hashing. In FSE, pages 54–72. 2008.

[MR09] D. Micciancio and O. Regev. Lattice-based cryptography. In Post Quantum Cryptography,
pages 147–191. Springer, February 2009.