被動安全加密
一個單獨的輕微優化涉及消息位元在噪聲下可恢復的編碼方式。在本綜述中,為簡單起見,將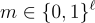
編碼為 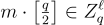 ,這導致了 logq 的乘法開銷,以及密文「前導碼」(preamble)
,這導致了 logq 的乘法開銷,以及密文「前導碼」(preamble)  的加法開銷。最近,Peikert [Pei14] 描述了一種更複雜的「調和」(reconciliation) 機制,該機制對消息進行逐位元編碼,使密文開銷僅為加法。該機制適用於任何 ℓ 值以及基本上任何(環-)LWE 密碼系統。
的加法開銷。最近,Peikert [Pei14] 描述了一種更複雜的「調和」(reconciliation) 機制,該機制對消息進行逐位元編碼,使密文開銷僅為加法。該機制適用於任何 ℓ 值以及基本上任何(環-)LWE 密碼系統。
16.1 生成新的 LWE 樣本:
指出 Regev 密碼系統的加密演算法(方程式 (15.2.3)) 隱含了一種方法來結束對它的介紹,該方法在給定足夠數量的初始樣本的情況下,為固定秘密和稍寬的高斯誤差分佈生成無限多個「新」LWE 樣本。更具體地說,零的加密 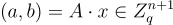 本質上是一個秘密為 s 的新 LWE 樣本,因為 a 與均勻分佈的距離可忽略不計且獨立於
本質上是一個秘密為 s 的新 LWE 樣本,因為 a 與均勻分佈的距離可忽略不計且獨立於  ,並且
,並且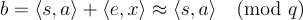
因此(a,b) 構成了 s 的一個有噪聲的線性方程式。然而,對於上述描述的系統,誤差項 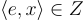 的分佈(在 x 的隨機選擇上)可能不太「好」,甚至可能隨 a 的值而變化。因此,以這種方式生成的樣本可能不完全符合我們通常所說的「新」LWE 樣本,即來自分佈
的分佈(在 x 的隨機選擇上)可能不太「好」,甚至可能隨 a 的值而變化。因此,以這種方式生成的樣本可能不完全符合我們通常所說的「新」LWE 樣本,即來自分佈  。
。
幸運的是,[GPV08, ACPS09],中利用 [Reg05] 的一個關鍵引理證明,一個稍加修改的過程確實生成了具有真實高斯誤差分佈的 LWE 樣本(達到可忽略的統計誤差)。應根據離散高斯 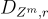 ,對於適當的
,對於適當的 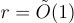 ,選擇 x,並在 A⋅x 的最後一個座標上添加一點「平滑」誤差。結果樣本中的誤差在統計上接近參數為
,選擇 x,並在 A⋅x 的最後一個座標上添加一點「平滑」誤差。結果樣本中的誤差在統計上接近參數為 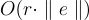 的高斯分佈,其中 e 是原始 LWE 樣本中的誤差向量。(要注意,只要這個原始誤差 e 相對較短,它可以來自任何分佈。)此外,當輸入矩陣 A 是均勻隨機的(而不是來自 LWE 分佈)時,相同的過程會產生幾乎均勻隨機且獨立於 A 的樣本。因此,該過程是 LWE 搜尋和判定形式的一種隨機化自歸約(randomized self-reduction)。
的高斯分佈,其中 e 是原始 LWE 樣本中的誤差向量。(要注意,只要這個原始誤差 e 相對較短,它可以來自任何分佈。)此外,當輸入矩陣 A 是均勻隨機的(而不是來自 LWE 分佈)時,相同的過程會產生幾乎均勻隨機且獨立於 A 的樣本。因此,該過程是 LWE 搜尋和判定形式的一種隨機化自歸約(randomized self-reduction)。
16.2 對偶 LWE 密碼系統
Gentry、Peikert 和 Vaikuntanathan(以下簡稱 GPV)[GPV08] 定義了一個基於 LWE 的公鑰加密方案,可以視為與上述 Regev [Reg05] 和 Peikert 等人 [PVW08] 的方案是「對偶」的。這些系統在以下意義上是對偶的:在上述方案中,公鑰具有非均勻(LWE)分佈和唯一的私鑰,但對於給定的公鑰,有許多加密隨機性的選擇可以產生相同的密文。相反,在 GPV 系統中,公鑰是均勻隨機的,有許多可能的私鑰,而產生特定密文的加密隨機性是唯一的。事實證明,擁有多個可能的私鑰對於構造各種更高級的密碼系統非常有用,如後續章節所述。
系統描述:
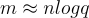 選擇一個均勻隨機的
選擇一個均勻隨機的 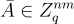 。在多用戶設定中,
。在多用戶設定中,  可以由可信方選擇並在所有用戶之間共享。私鑰是一個均勻隨機的
可以由可信方選擇並在所有用戶之間共享。私鑰是一個均勻隨機的  ,而公鑰是
,而公鑰是 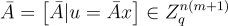 。請注意,公鑰和私鑰滿足關係
。請注意,公鑰和私鑰滿足關係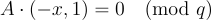
請注意,為給定的公鑰  、u 找到有效的私鑰本質上是(非齊次)SIS 問題。
、u 找到有效的私鑰本質上是(非齊次)SIS 問題。
要加密一個位元  選擇一個 LWE 秘密
選擇一個 LWE 秘密 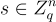 ,並輸出密文
,並輸出密文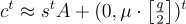
(16.2.5)
其中近似隱藏了從 LWE 誤差分佈 χ 抽取的獨立誤差。
要使用私鑰 x 解密,計算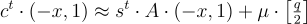
方程式 (16.2.5);x 是短的。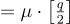
方程式 (16.2.4),結果是0,因此可以得出以上結論。
並測試結果模 q 後更接近 0 還是 q/2。請注意,上述近似中的總誤差基本上與 Regev 系統中的相同。
安全性:
該對偶密碼系統在語義上對抗被動竊聽者是安全的,假設判定-LWE n,q,χ,m+1 是難解的。證明過程與 Regev 系統的證明(參見第 5.2.1 節)非常相似,但某些步驟的順序有所調整。
兩個主要思想是:
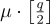 項)構成了一組 LWE 樣本,這些樣本與均勻分佈不可區分,因此隱藏了消息。由於許多後續構造建立在對偶密碼系統及其安全性證明之上,這裡給出相當詳細的概述,再次考慮一系列產生公鑰
項)構成了一組 LWE 樣本,這些樣本與均勻分佈不可區分,因此隱藏了消息。由於許多後續構造建立在對偶密碼系統及其安全性證明之上,這裡給出相當詳細的概述,再次考慮一系列產生公鑰 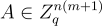 和密文
和密文 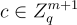 的混合實驗:
的混合實驗:在第一個混合實驗中,公鑰 A 是均勻隨機選擇的,而不是通過金鑰生成演算法生成為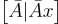
密文 c 是通過在 A 下以通常方式加密位元 μ 生成的。這個混合實驗在統計上與真實實驗不可區分。與之前的證明一樣,這源於 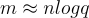 足夠大這一事實,以及正則性引理。
足夠大這一事實,以及正則性引理。
在下一個混合實驗中,公鑰 A 保持均勻隨機,現在密文 c 也是均勻選擇的,並且獨立於 A。在 LWE 假設下,這個混合實驗與前一個實驗是不可區分的。這通過一個直接的歸約得出:給定從 LWE 或均勻分佈抽取的 m+1 個樣本 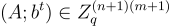
可以通過輸出 A 作為公鑰和 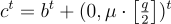 ,作為密文來模擬前一個混合實驗或這個實驗(分別)。(請注意,在均勻情況下,添加固定項保持了 b 的均勻性。)因此,任何假設的區分器用於區分這兩個混合實驗都將直接轉化為對判定-LWE 問題具有相同優勢的區分器。
,作為密文來模擬前一個混合實驗或這個實驗(分別)。(請注意,在均勻情況下,添加固定項保持了 b 的均勻性。)因此,任何假設的區分器用於區分這兩個混合實驗都將直接轉化為對判定-LWE 問題具有相同優勢的區分器。
因為上述實驗對於任何固定位元 μ 是不可區分的,並且最後一個實驗完全與 μ 無關,所以對於 μ=0,1 的兩個真實實驗也是不可區分的。
變體:
對偶 LWE 密碼系統的幾個變體值得簡要提及:
與 Regev 的系統一樣,存在一個一次加密 ℓ 個位元的對偶系統的攤銷版本。這裡使用一個均勻隨機的私鑰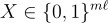
和公鑰 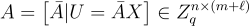 ,然後消息的每個位元由對應的(有噪聲的)
,然後消息的每個位元由對應的(有噪聲的)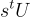 條目隱藏。
條目隱藏。
私鑰 X 的條目不必是二進位的或均勻的,但可以從任何小整數的分佈中選擇,使得 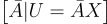
在統計上接近均勻。最值得注意的是,當 X 的條目從例如 Z 上的離散高斯分佈中選擇時,該方案可以成為基於身份的(identity-based)。
更緊湊的 LWE 密碼系統
Lindner 和 Peikert [LP11] 提出了一種公鑰密碼系統,其中公鑰,以及私鑰和/或密文,比上述基於 LWE 的方案小大約 logq 倍,對於典型的參數選擇,這大約是十倍或更多。該系統將 Alekhnovich [Ale03] 的基於編碼的密碼系統和 Lyubashevsky、Palacio 和 Segev [LPS10] 的基於子集和的密碼系統及其安全性證明策略應用於 LWE。特別是,與上述描述的系統相比,對於給定的公鑰和密文,私鑰和加密隨機性都是唯一的。
系統描述:
令 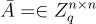
為一個(可能共享的)均勻隨機方矩陣。私鑰是一個向量 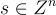 ,其座標從誤差分佈 χ 中獨立抽取,公鑰是
,其座標從誤差分佈 χ 中獨立抽取,公鑰是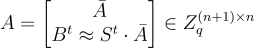 ,其中近似隱藏了從 χ 抽取的獨立誤差。請注意,私鑰和公鑰滿足關係
,其中近似隱藏了從 χ 抽取的獨立誤差。請注意,私鑰和公鑰滿足關係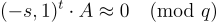
(16.2.7)
要加密一個位元 μ∈{0,1},選擇一個 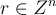 ,其座標從誤差分佈中抽取,並輸出一個密文
,其座標從誤差分佈中抽取,並輸出一個密文
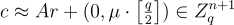
(16.2.8)
其中近似隱藏了從 χ 抽取的獨立誤差。
要使用私鑰 s 解密,計算
其中第一個近似依賴於方程式 (16.2.8) 和 s 的短性,第二個依賴於方程式 (16.2.7) 和 r 的短性。
與先前的方案類似,存在一個攤銷變體,每個密文可以加密 ℓ 個位元。這裡私鑰是獨立誤差項的矩陣 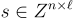 公鑰是
公鑰是 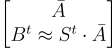
分析
上述方案在語義上對抗被動竊聽者是安全的,假設判定-LWE 是難解的。證明與之前描述的方案略有不同: 它兩次依賴於標準形式 LWE 假設,並且不需要統計正則性引理。更詳細一點,首先注意在 LWE 假設下,公鑰與均勻分佈是不可區分的。因此考慮一個公鑰是均勻隨機的混合實驗:那麼公鑰和密文(忽略  項)一起正好構成 n+1 個 LWE 樣本,根據假設這些樣本與均勻分佈不可區分,因此它們隱藏了消息位元。
項)一起正好構成 n+1 個 LWE 樣本,根據假設這些樣本與均勻分佈不可區分,因此它們隱藏了消息位元。
請注意,如果希望從定理 4.2.4 獲得最壞情況硬度保證,那麼 r,s 的條目(從 χ 抽取)的幅度需要大約為 n 的量級。因此,解密關係中的累積誤差比先前的基於 LWE 的方案大約大一個 n 因子。這導致了稍大的模數 q,從而導致公鑰和密文的 LWE 誤差率更小,這使得底層最壞情況格問題的近似因子 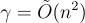 相對於
相對於 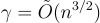 稍鬆。然而,在歸一化到針對具體攻擊的相同估計硬度後,緊湊方案仍然具有更小的金鑰和密文。
稍鬆。然而,在歸一化到針對具體攻擊的相同估計硬度後,緊湊方案仍然具有更小的金鑰和密文。
16.2.4 環-LWE 密碼系統
使用之前概述的 LWE 和環-LWE 之間的對應關係,絕大多數基於 LWE 的方案和應用可以機械地轉換為更緊湊和高效的方案,這些方案在對應的環-LWE 假設下保持安全。
緊湊的環-LWE 加密
緊湊基於 LWE 的密碼系統的環-LWE 類比相對容易描述和分析。該系統首先在 [LPR10] 中針對最簡單的分圓環 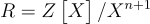 ,(n 是 2 的冪)進行描述,並在 [LPR13] 中針對任意分圓環進行了全面描述。簡而言之,該系統工作如下:公鑰是一個標準形式的環-LWE 樣本
,(n 是 2 的冪)進行描述,並在 [LPR13] 中針對任意分圓環進行了全面描述。簡而言之,該系統工作如下:公鑰是一個標準形式的環-LWE 樣本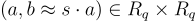
對於某個(可能共享的)均勻隨機 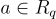 和短的私鑰
和短的私鑰 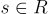 ,其中 s 和近似誤差都從 χ 抽取。要加密消息
,其中 s 和近似誤差都從 χ 抽取。要加密消息 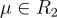 ,對應於一個 n 位元字串,生成一個密文
,對應於一個 n 位元字串,生成一個密文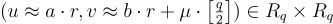
其中 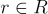 ,且近似誤差從 χ 抽取。解密通過計算
,且近似誤差從 χ 抽取。解密通過計算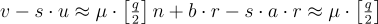
並通過去除近似誤差來恢復 μ 來實現。(在一般分圓環的構造中,獲得最緊密的參數有些微妙,系統需要稍作調整;詳見 [LPR13]。)按時間順序,環-LWE 類比實際上是在基於 LWE 的系統之前被發現的,後者是從前者「反向移植」的。
環-LWE 與 NTRU 的結合:
Stehle 和 Steinfeld [SS11] 給出了一個 NTRU 密碼系統的變體,該變體在環-LWE 假設下具有安全性證明。在他們的系統中,與 NTRU 一樣,公鑰是兩個「有點短」的多項式的比率 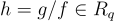 。然而這裡 f 和 g 的係數被選擇為具有大約
。然而這裡 f 和 g 的係數被選擇為具有大約 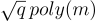 的幅度,使得
的幅度,使得 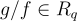 。在統計上非常接近均勻隨機。(相反,在 NTRU 中,係數非常小,並且 g/f 被猜想在計算上與均勻不可區分。)證明這一統計事實是主要的技術障礙;一旦獲得,從環-LWE 導出的語義安全性就相對容易了。與上述描述的環-LWE 密碼系統相比,這裡的公鑰和密文各自僅為一個環元素。然而,為了同時獲得統計特性和正確性,參數必須顯著更大,以至於該方案在具體效率上不如其他環-LWE 方案。
。在統計上非常接近均勻隨機。(相反,在 NTRU 中,係數非常小,並且 g/f 被猜想在計算上與均勻不可區分。)證明這一統計事實是主要的技術障礙;一旦獲得,從環-LWE 導出的語義安全性就相對容易了。與上述描述的環-LWE 密碼系統相比,這裡的公鑰和密文各自僅為一個環元素。然而,為了同時獲得統計特性和正確性,參數必須顯著更大,以至於該方案在具體效率上不如其他環-LWE 方案。
正則性:
在將其他基於 LWE 的應用轉換為環-LWE 時,一個微妙之處在於某些方案需要針對環-SIS 函數 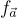 (方程式 (11.1)) 的適當正則性(或「剩餘雜湊」)引理。對於環來說,這樣的引理比對於像
(方程式 (11.1)) 的適當正則性(或「剩餘雜湊」)引理。對於環來說,這樣的引理比對於像 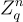 ,這樣的加法群要難證明得多,主要是因為對於通常使用的參數,環
,這樣的加法群要難證明得多,主要是因為對於通常使用的參數,環 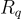 ,遠非一個域,即它有許多零因子。Micciancio [Mic02] 為此類環給出了第一個正則性引理,其中 q 是質整數。一個缺點是證明依賴於使用「短」環元素
,遠非一個域,即它有許多零因子。Micciancio [Mic02] 為此類環給出了第一個正則性引理,其中 q 是質整數。一個缺點是證明依賴於使用「短」環元素 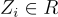 。這些元素當視為多項式時,在一個 poly(n) 大小的區間內具有均勻隨機的整數係數。然而,許多應用需要或最適合使用高斯分佈的環元素。[LPR13] 中給出了一個適用於此設置的後續正則性引理。它依賴於標準形式的環-SIS 實例:
。這些元素當視為多項式時,在一個 poly(n) 大小的區間內具有均勻隨機的整數係數。然而,許多應用需要或最適合使用高斯分佈的環元素。[LPR13] 中給出了一個適用於此設置的後續正則性引理。它依賴於標準形式的環-SIS 實例: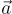 ,其中第一個
,其中第一個 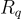 分量是單位元,並且它仍然要求
分量是單位元,並且它仍然要求 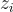 具有多項式級大的整數係數。如果
具有多項式級大的整數係數。如果 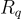 是一個域或「接近」於域,那麼標準的剩餘雜湊引理就足夠了,並且能產生良好的參數。
是一個域或「接近」於域,那麼標準的剩餘雜湊引理就足夠了,並且能產生良好的參數。
參考資料
[Pei14] C. Peikert. Lattice cryptography for the Internet. In PQCrypto, pages 197–219. 2014.
[GPV08] C. Gentry, C. Peikert, and V. Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. In STOC, pages 197–206. 2008.
[ACPS09] B. Applebaum, D. Cash, C. Peikert, and A. Sahai. Fast cryptographic primitives and circularsecure encryption based on hard learning problems. In CRYPTO, pages 595–618. 2009.
[Reg05] O. Regev. On lattices, learning with errors, random linear codes, and cryptography. J. ACM, 56(6):1–40, 2009. Preliminary version in STOC 2005.
[LP11] R. Lindner and C. Peikert. Better key sizes (and attacks) for LWE-based encryption. In CT-RSA, pages 319–339. 2011.
