回顧之前曾用 random 模組打造抽籤程式，今天就來聊聊隨機數與模擬應用。

隨機數的概念

隨機數常用在統計學、數學和電腦科學中，但它其實比我們想像中難實現。在日常生活中，我們經常接觸到兩種不同的隨機性：真隨機和假隨機。

真隨機True Random

真隨機指的是無法預測、沒有任何規律可循的隨機性，來自於物理世界中那些本質上就具有不可預測性的現象，像是：原核子衰變的時間、量子系統的狀態本身等都是有隨機性的，我們無法從已知資訊中預測下一個隨機數是甚麼，也無法重新生成一模一樣的隨機數序列。

真隨機的應用通常為需要極高安全性的場景，例如：

• 加密：用於生成加密金鑰，確保金鑰的不可預測性。
• 線上遊戲或抽獎： 確保抽獎結果的公平性。
• 科學研究： 模擬或實驗需要真正的隨機性。

假隨機Pseudo-random

假隨機看似隨機，但實際上是透過一個確定性演算法產生的數列。它之所以被稱為「假」隨機，是因為只要知道演算法和初始的「種子」（seed），就可以精確地重現整個數列。
跟真隨機的不同點在於假隨機是可以預測出的，只要知道seed就可以推算完整的數列，這也代表我們若使用相同的seed，每次都會產生完全相同的隨機數列。另外，假隨機數列在經過一定長度後會重複，有著週期性的特點。

假隨機的應用在大多數電腦應用中都非常常見，因為它產生速度快且可重複，這對除錯和測試很有幫助，例如：

• 模擬和遊戲：像遊戲中敵人出現的位置、掉落物品的機率。
• 軟體測試：確保每次測試都能用相同的隨機數據。
• 統計模擬：例如蒙地卡羅模擬（Monte Carlo simulation）。

Python random 模組功能簡介

回到 Python 的內建模組──random，它提供了多種生成假隨機數的功能，這意味著它的隨機數是由演算法產生的，如果使用相同的seed，每次都會得到相同的結果，這在除錯和測試時特別方便。
以下是幾個常用的random功能：

1. random.random()

這個函式會回傳一個介於 0.0 到 1.0 之間的浮點數(包含 0.0，但不包含 1.0)。

import random
print(random.random())  # 可能輸出：0.8351174623796695

2. random.randint(a, b)

這個函式會回傳一個介於 a 和 b 之間（包含 a 和 b）的整數。

import random
print(random.randint(1, 10))  # 可能輸出：5

3. random.choice(seq)

這個函式會從一個序列（列表、元組或字串）中隨機選擇一個元素回傳。

import random
my_list = ['蘋果', '香蕉', '橘子']
print(random.choice(my_list))  # 可能輸出：香蕉

4. random.shuffle(seq)

這個函式會直接打亂一個序列的順序，但只適用於可變的序列，例如列表（list），它不會回傳任何東西。

import random
my_list = ['A', 'B', 'C', 'D']
random.shuffle(my_list)
print(my_list)  # 可能輸出：['C', 'A', 'D', 'B']

5. random.sample(seq, k)

這個函式會從一個序列中隨機選擇 k 個不重複的元素，並以列表（list）的形式回傳。

import random
my_list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sample_items = random.sample(my_list, 3)
print(sample_items)  # 可能輸出：[7, 3, 9]

應用範例

接下來，我們來看看電腦是怎麼產生「假」隨機數的，這裡會用兩個例子來模擬：丟硬幣和擲骰子。
藉由記錄丟硬幣時正面反面各出現幾次，還有擲骰子每個點數出現的次數，然後把這些數據做成長條圖，看看它們的分布長什麼樣子。

丟硬幣

主程式碼：

import random
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rcParams['font.family'] = 'Microsoft JhengHei' # 微軟正黑體

# 模擬拋硬幣 1000 次
trials = 1000
results = {"正面": 0, "反面": 0}

for _ in range(trials):
    coin = random.choice(["正面", "反面"])
    results[coin] += 1

長條圖程式碼:

# 畫長條圖
plt.bar(results.keys(), results.values(), color=["skyblue", "lightcoral"])
plt.title("拋硬幣分布 (1000 次)")
plt.xlabel("結果")
plt.ylabel("出現次數")
plt.show()

結果：

我們可以看到正反面大概接近一半，但不會完全一樣。

擲骰子

主程式碼：

import random
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rcParams['font.family'] = 'Microsoft JhengHei' # 微軟正黑體
# 模擬擲骰子 6000 次
trials = 6000
results = {i: 0 for i in range(1, 7)}

for _ in range(trials):
    dice = random.randint(1, 6)
    results[dice] += 1

長條圖程式碼：

# 畫長條圖
plt.bar(results.keys(), results.values(), color="lightgreen")
plt.title("骰子分布 (6000 次)")
plt.xlabel("點數")
plt.ylabel("出現次數")
plt.show()

結果：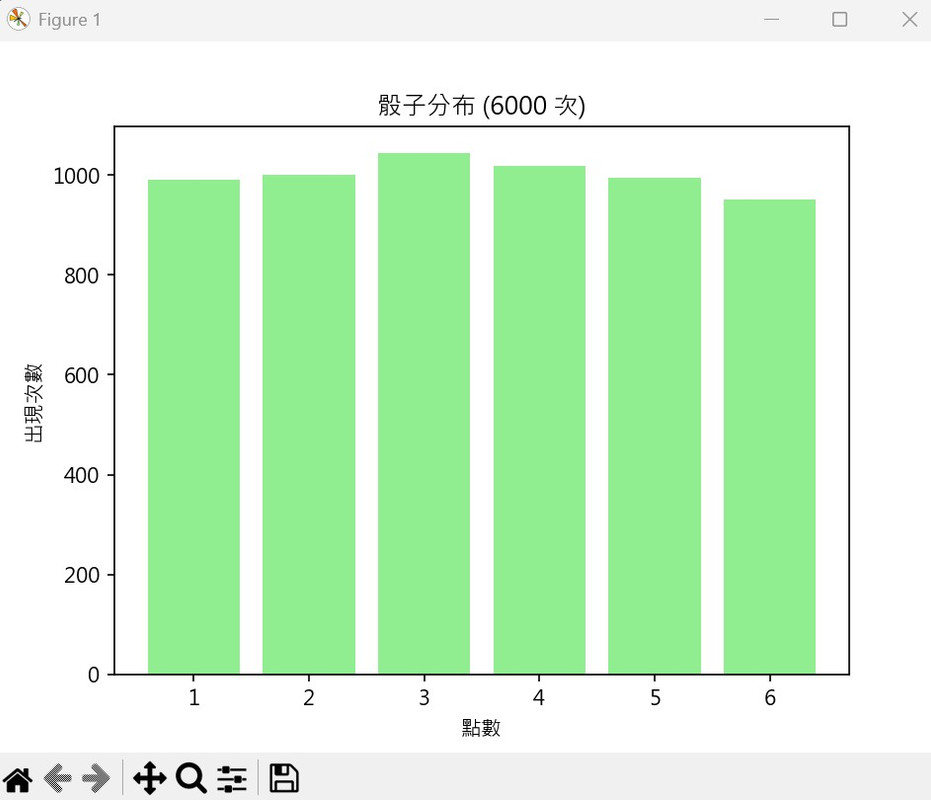

我們能看到每個點數的次數差不多，但還是會有些小波動。若隨著試驗次數增加，分布會更趨近平均。

完成這次實驗後，最明顯的感受是：雖然單次結果看似完全不可預測，但當實驗次數累積到幾千、甚至上萬次時，分布就會逐漸趨近於理論上的平均，這顯示了「隨機」背後其實蘊含著一種規律。
同時透過電腦模擬的對比，也讓人想到：即使是假隨機，只要樣本量足夠，依然能展現出與真隨機相似的統計規律。
這樣的觀察更引發一個有趣的思考——在日常生活中，那些看似偶然的事件，是否也可能遵循著類似的大數法則？這或許正是我們持續探索「隨機」與「規律」之間的動力。