經過上一篇針對基本密碼學構造中的主動安全加密部分的講解,相信大家都對主動安全加密部有初步的認識,接下來在這一篇就會對主動安全加密作深入的講解,希望大家可以更進一步認識更多相關知識。
18.1 其他取樣演算法
自從為密碼學目的引入離散高斯取樣 [GPV08] 以來,已經提出了許多改進和替代演算法。
在上一篇中的定理 17.4.1.2 中描述的用於離散高斯取樣的隨機化最近平面演算法通常相當低效:它需要非常高精度的算術來儲存和操作(Gram-Schmidt 正交化基底的一個適當表示),並且它涉及 n 個順序迭代,每個迭代都需要進行高精度向量的 n 維內積。此外,這種超二次方的運行時間持續存在於環設定中(例如,對於環-SIS/LWE),而相比之下,所有其他常用的環操作僅是擬線性時間。
Peikert [Pei10] 給出了一個更高效且可並行的離散高斯取樣演算法,該演算法在環設定中也是擬線性時間。作為一個說明性的初步嘗試,為了使用 L 的短基底 S 並行地從 c+L 中取樣,人們可能會嘗試獨立地隨機捨入基底向量的每個係數,即令 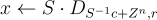 對於某個適當的
對於某個適當的 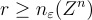 。這會產生 c+L 中的一個短隨機元素,但不幸的是,由於乘以 S,分佈是「偏斜的」。更正式地說,它是一個 非球形 (non-spherical) 的離散高斯分佈,其協方差矩陣為
。這會產生 c+L 中的一個短隨機元素,但不幸的是,由於乘以 S,分佈是「偏斜的」。更正式地說,它是一個 非球形 (non-spherical) 的離散高斯分佈,其協方差矩陣為 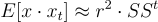 這會洩露很多關於 S 的資訊。
這會洩露很多關於 S 的資訊。
[Pei10] 中的主要思想是添加一個適當分佈的 擾動 (perturbation) 項來「去偏斜」x 的分佈,使其成為球形的。更正式地說,要從 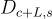 中取樣,執行以下操作:
中取樣,執行以下操作:
這種使用擾動來隱藏關於 S 的資訊的想法,其靈感大致來自於 NTRUSign [HHGP+03] 中包含的另一種擾動技術(但在技術上非常不同),但後者已被證明是不安全的 [MPSW09, Wan10, DN12b]。
在離線階段(在目標陪集 c+L 已知之前),選擇一個具有協方差
的高斯擾動 p。
在線上階段(當 c+L 已知時),輸出 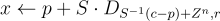
注意,x 的支撐集是 c+L,符合期望。此外,[Pei10] 中的一個「卷積 (convolution)」引理本質上說明, 就像對於 連續 高斯分佈一樣,離散高斯加項的協方差是 可加 的,因此 x 是具有所需協方差 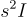 的離散高斯分佈。最後,請注意,擾動項 p 的分佈是明確定義的,當且僅當
的離散高斯分佈。最後,請注意,擾動項 p 的分佈是明確定義的,當且僅當 是正定的,這成立若且唯若
是正定的,這成立若且唯若 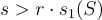 其中
其中 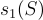 表示 S 的最大奇異值(或譜範數)。因此,取樣器的最終高斯參數與
表示 S 的最大奇異值(或譜範數)。因此,取樣器的最終高斯參數與 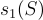 成正比,而不是像定理 17.4.1.2 ([GPV08]) 中那樣與
成正比,而不是像定理 17.4.1.2 ([GPV08]) 中那樣與  成正比。
成正比。
隨後,Ducas 和 Nguyen [DN12a] 給出了一種技術,使用浮點算術(FPA)優化(在對數因子範圍內)隨機化最近平面演算法的漸近平均情況運行時間,以及 Peikert 卷積取樣器的離線階段。他們的方法通過一種「惰性 (laziness)」技術將低精度和高精度 FPA 結合起來,通常保持低精度,並且在實踐中可以使用標準 IEEE 雙精度實現。
在另一個方向上,Brakerski 等人 [BLP+13] 給出了隨機化最近平面演算法的改進版本,該版本使用拒絕取樣(rejection sampling)來取樣參數小至 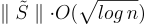 比定理 17.4.1.2 ([GPV08]) 節省了一個略超常數的
比定理 17.4.1.2 ([GPV08]) 節省了一個略超常數的  因子的離散高斯分佈,並且其統計誤差可以任意接近於零。然而,這些更精確的界限是以較大的運行時間和演算法複雜度為代價的。
因子的離散高斯分佈,並且其統計誤差可以任意接近於零。然而,這些更精確的界限是以較大的運行時間和演算法複雜度為代價的。
最近,Lyubashevsky 和 Wichs [LW15] 給出了在離散高斯分佈以外的分佈(例如,在一個盒子內均勻分佈)下從晶格陪集取樣短向量的演算法。此類取樣器可用於提供原像可採樣函數的替代實例化。與先前的離散高斯取樣器相比,這些新取樣器的主要優勢在於其實現相對簡單且避免了高精度算術。它們的主要缺點在於它們產生的向量較長,其長度因子最多可達晶格維度的線性倍數,這對應於更差的安全性(因此需要更大的金鑰來補償)。
最後,Ducas 和 Prest [DP15] 最近研究了一種針對在環上定義的晶格(例如 NTRU 晶格)的「混合 (hybrid)」取樣器,該取樣器結合了最近平面取樣器和卷積取樣器。他們表明,就取樣品質和漸近效率而言,混合方法可以同時獲得先前兩種演算法的最佳特性。
18.2 小工具陷門 (Gadget Trapdoors)
現在從作為通用晶格陷門的短基底,轉向基於「小工具 (gadget)」的陷門,用於 q 元 SIS/LWE 晶格,如 [MP12] 中所開發,並建立在幾項相關研究 [Ajt99, AP09, PW08, ABB10] 的技術之上。
小工具 (Gadgets):
第一個主要思想是,存在特殊的、結構化的矩陣 G,稱為「小工具」,對於它們求解 SIS 和 LWE 是 容易的。最簡單的小工具如下:對於給定的模數 q,定義向量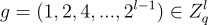
其中  現在觀察到,給定任何
現在觀察到,給定任何 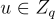 可以找到一個短的解
可以找到一個短的解 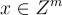 滿足
滿足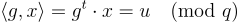
例如,令 x 對應於 u 在 {0,…,q−1} 中的標準代表元的二進位表示。換句話說,相對於單行奇偶校驗「矩陣」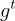 ,求解 SIS 問題是容易的。此外,容易從解晶格陪集
,求解 SIS 問題是容易的。此外,容易從解晶格陪集  上的離散高斯分佈中隨機取樣。
上的離散高斯分佈中隨機取樣。
再思考一下會發現,相對於 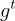
求解 LWE 也是容易的。為簡單起見,假設 q=2ℓ;那麼給定任何 且誤差在區間
且誤差在區間  內,可以從
內,可以從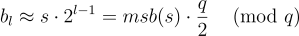
恢復 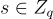 的最高有效位(most-significant bit)。然後可以從
的最高有效位(most-significant bit)。然後可以從 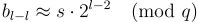 恢復 s 的下一個最高有效位,依此類推。(這一切也可以推廣到非二的冪模數,但在技術上稍微複雜一些。)
恢復 s 的下一個最高有效位,依此類推。(這一切也可以推廣到非二的冪模數,但在技術上稍微複雜一些。)
將上述所有內容擴展到相對於塊對角 小工具矩陣 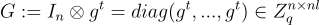 的 n 維 SIS 和 LWE,只需按塊處理:對於 LWE,給定
的 n 維 SIS 和 LWE,只需按塊處理:對於 LWE,給定 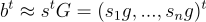 只需從 b 的相應塊中恢復每個
只需從 b 的相應塊中恢復每個 
對於 SIS,要為給定的 找到 Gx=u 的短解,只需為每個分量
找到 Gx=u 的短解,只需為每個分量  找到
找到 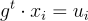 的短解並連接結果。將此操作用「分解 (decomposition)」函數表示是很方便的:
的短解並連接結果。將此操作用「分解 (decomposition)」函數表示是很方便的: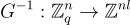
其中符號選擇的解釋源於關係 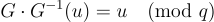 強調
強調 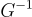 不是一個 矩陣,而是一個將模 q 輸入映射到短整數向量的 函數。根據上下文
不是一個 矩陣,而是一個將模 q 輸入映射到短整數向量的 函數。根據上下文 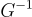 操作甚至可以是隨機化的,例如,它可以取樣一個高斯分佈的解。
操作甚至可以是隨機化的,例如,它可以取樣一個高斯分佈的解。
最後,觀察到給定任何可逆矩陣  相對於矩陣
相對於矩陣 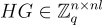 ,SIS 和 LWE 仍然容易求解。具體來說,要求解 (HG)x=u,只需輸出
,SIS 和 LWE 仍然容易求解。具體來說,要求解 (HG)x=u,只需輸出 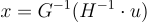 而給定
而給定 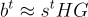 首先通過相對於 G 求解來恢復
首先通過相對於 G 求解來恢復  然後將解乘以
然後將解乘以 
18.3 陷門定義和使用:
下一個主要思想是,一個奇偶校驗矩陣 A 可以「隱藏」公共小工具矩陣 G 的(一個倍數)。一個 陷門 只是一個短的線性變換,用於揭示小工具。
定義 18.3.1:
奇偶校驗矩陣 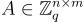 的一個 陷門 是任何足夠「短」的整數矩陣
的一個 陷門 是任何足夠「短」的整數矩陣 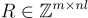 使得
使得 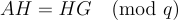 方程 (18.3.2)
方程 (18.3.2)
顯然,x 是短的,因為 R 和 w 是短的,具體來說  並且根據方程 (18.3.2),
並且根據方程 (18.3.2),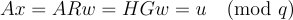
抽樣一個 高斯分佈的 SIS 解則稍微更微妙一些。在上面的方法中,可以只抽樣一個高斯分佈的解 w,但這樣 x=Rw 的分佈會被陷門 R 「偏斜」,從而洩露關於 R 的資訊。為了校正這種偏斜,可以使用 [Pei10] 的「卷積」技術(在 18.3.2 的最後部分描述):首先選擇一個適當分佈的擾動向量 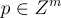 然後抽樣一個高斯解
然後抽樣一個高斯解 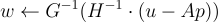
最後輸出 x=p+Rw。通過讓 p 具有適當的分佈,可以使得到的 x 的分佈成為任何所需參數超過 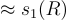 的離散高斯分佈。
的離散高斯分佈。
類似地,可以使用陷門來求解相對於 A 的 LWE。給定 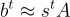 ,簡單地將其轉換為
,簡單地將其轉換為  ,然後通過求解相對於 HG 的 LWE 來找到 s,如上所述。請注意,從第一個近似值到第二個近似值,誤差最多擴大了
,然後通過求解相對於 HG 的 LWE 來找到 s,如上所述。請注意,從第一個近似值到第二個近似值,誤差最多擴大了 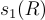 倍,因此相對於 A 可以處理的誤差大約比相對於 G 可以處理的誤差小
倍,因此相對於 A 可以處理的誤差大約比相對於 G 可以處理的誤差小 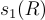 倍。
倍。
18.4 陷門生成 (Trapdoor generation):
現在描述如何構造一個(近似)均勻隨機的奇偶校驗矩陣 A 連同一個具有所需標籤 H 的陷門 R。從選擇一個均勻隨機的  其中
其中 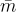 足夠大,且
足夠大,且  可以在許多矩陣和陷門之間共享,和一個短的隨機整數矩陣
可以在許多矩陣和陷門之間共享,和一個短的隨機整數矩陣 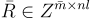
例如,具有離散高斯項的矩陣,在開始。然後令 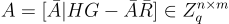 其中
其中 
根據構造,立即有 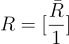 是 A 的一個帶標籤 H 的陷門。其次,根據隨機矩陣理論的標準界限(例如,參見 [Ver12]),以非常高的概率,譜範數
是 A 的一個帶標籤 H 的陷門。其次,根據隨機矩陣理論的標準界限(例如,參見 [Ver12]),以非常高的概率,譜範數 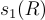 是小的,例如,當 Rˉ 的項是參數為 s 的次高斯分佈時,它是
是小的,例如,當 Rˉ 的項是參數為 s 的次高斯分佈時,它是 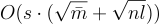
最後,對於 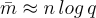 的適當選擇和
的適當選擇和  的分佈,矩陣 A 在
的分佈,矩陣 A 在 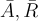 的選擇下在統計上非常接近均勻。特別是,標籤 H 的選擇在統計上被 A 本身隱藏,這在後面描述的許多應用的安全性證明中是一個重要的事實。
的選擇下在統計上非常接近均勻。特別是,標籤 H 的選擇在統計上被 A 本身隱藏,這在後面描述的許多應用的安全性證明中是一個重要的事實。
最後,提到,通過使用 其中
其中  是一個均勻隨機的 方 矩陣)代替上面的矩形矩陣
是一個均勻隨機的 方 矩陣)代替上面的矩形矩陣  很容易調整上述構造,以在正規形式 (normal-form) LWE 假設下得到一個在計算上是偽隨機的較小奇偶校驗矩陣。
很容易調整上述構造,以在正規形式 (normal-form) LWE 假設下得到一個在計算上是偽隨機的較小奇偶校驗矩陣。
18.5 穿孔 (Puncturing):
上述構造允許一種代數的「陷門穿孔」技術,這是基於 LWE 的有損陷門函數 [PW08] 和緊湊 (H)IBE [ABB10] 的主要工具,也在許多其他工作中使用。注意,在上述構造中,對於矩陣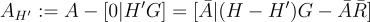
當中 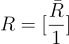 仍然是帶標籤
仍然是帶標籤  的陷門。
的陷門。
通過讓 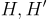 來自於
來自於  中具有 可逆差異 (invertible differences) 的矩陣族 — — 即任何兩個不同矩陣之間的差是可逆的,在
中具有 可逆差異 (invertible differences) 的矩陣族 — — 即任何兩個不同矩陣之間的差是可逆的,在  上,看到矩陣 AH′ 在 R 是陷門的意義上被「穿孔」,但 除了其中一個 之外,即
上,看到矩陣 AH′ 在 R 是陷門的意義上被「穿孔」,但 除了其中一個 之外,即  具有可逆差異屬性的矩陣族可以構造,例如從有限域
具有可逆差異屬性的矩陣族可以構造,例如從有限域 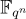
(其中 q 是質數)構造如下。將 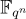 視為在
視為在  上具有某個固定基底的 n 維向量空間,並讓每個
上具有某個固定基底的 n 維向量空間,並讓每個 
對應於表示乘以 h 的  -線性變換的 n 乘 n 矩陣。因為這個對應是從
-線性變換的 n 乘 n 矩陣。因為這個對應是從 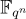 到
到  的單射環同態,並且每個非零域元素都是可逆的,所以這個族具有可逆差異。
的單射環同態,並且每個非零域元素都是可逆的,所以這個族具有可逆差異。
18.6 擴展和隨機化陷門:
通過提及來結束對小工具陷門的介紹:就像短基底陷門一樣,存在非常簡單的方法來擴展和重新隨機化小工具陷門,這些方法在分層 IBE 和其他應用中很有用。
給定 A 的一個陷門 R,有以下內容:
矩陣  顯然是任何擴展
顯然是任何擴展  的陷門(具有與 R 相同的標籤)。
的陷門(具有與 R 相同的標籤)。
很容易生成一個新的隨機陷門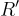
具有任何所需的標籤 H′,該陷門不會洩露關於 R 的任何資訊(除了 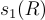 的上限),只需使用 R 來取樣
的上限),只需使用 R 來取樣  的高斯解。
的高斯解。
或者,要生成一個形式為 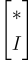 的隨機陷門(這是上面描述的穿孔技術所需要的),對於任意擴展
的隨機陷門(這是上面描述的穿孔技術所需要的),對於任意擴展  可以取樣一個高斯分佈的解 R′ 滿足
可以取樣一個高斯分佈的解 R′ 滿足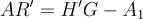
那麼  是 A′ 的帶標籤 H′ 的陷門。
是 A′ 的帶標籤 H′ 的陷門。
參考資料
[GPV08] C. Gentry, C. Peikert, and V. Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. In STOC, pages 197–206. 2008.
[Pei10] C. Peikert. An efficient and parallel Gaussian sampler for lattices. In CRYPTO, pages 80–97.2010
[HHGP+03] J. Hoffstein, N. Howgrave-Graham, J. Pipher, J. H. Silverman, and W. Whyte. NTRUSIGN: Digital signatures using the NTRU lattice. In CT-RSA, pages 122–140. 2003.
[MPSW09] T. Malkin, C. Peikert, R. A. Servedio, and A. Wan. Learning an overcomplete basis: Analysis of lattice-based signatures with perturbations, 2009. Manuscript.
[DN12b] L. Ducas and P. Q. Nguyen. Learning a zonotope and more: Cryptanalysis of NTRUSign
countermeasures. In ASIACRYPT, pages 433–450. 2012.
[DN12a] L. Ducas and P. Q. Nguyen. Faster Gaussian lattice sampling using lazy floating-point arithmetic. In ASIACRYPT, pages 415–432. 2012.
[BLP+13] Z. Brakerski, A. Langlois, C. Peikert, O. Regev, and D. Stehle. Classical hardness of learning with errors. In STOC, pages 575–584. 2013.
[LW15] V. Lyubashevsky and D. Wichs. Simple lattice trapdoor sampling from a broad class of
distributions. In PKC, pages 716–730. 2015.
[DP15] L. Ducas and T. Prest. A hybrid Gaussian sampler for lattices over rings. Cryptology ePrint Archive, Report 2015/660, 2015.
[MP12] D. Micciancio and C. Peikert. Trapdoors for lattices: Simpler, tighter, faster, smaller. In EUROCRYPT, pages 700–718. 2012.
[Ajt99] M. Ajtai. Generating hard instances of the short basis problem. In ICALP, pages 1–9. 1999.
[AP09] J. Alwen and C. Peikert. Generating shorter bases for hard random lattices. Theory of Computing Systems, 48(3):535–553, April 2011. Preliminary version in STACS 2009.
[PW08] C. Peikert and B. Waters. Lossy trapdoor functions and their applications. SIAM J. Comput., 40(6):1803–1844, 2011. Preliminary version in STOC 2008.
[ABB10] S. Agrawal, D. Boneh, and X. Boyen. Efficient lattice (H)IBE in the standard model. In EUROCRYPT, pages 553–572. 2010.
[Ver12] R. Vershynin. Compressed Sensing, Theory and Applications, chapter 5, pages 210–268.
Cambridge University Press, 2012. Available at http ://www-personal.umich.edu/
romanv/papers/non-asymptotic-rmt-plain.pdf.
