講了很多理論之後，這篇會與大家講一下相關的應用，究竟 Lattice 的應用是什麼。

19 數字簽章和基於身份的加密
在這裡描述一些密碼學應用，包括直接從上一小節描述的陷門函數和技術產生的簽章和基於身份的加密方案。

19.1 簽章 (Signatures)
在高層次上，GPV 簽章方案是通過將上幾篇中基於晶格的原像可採樣函數插入到經典的「雜湊並簽署 (hash-and-sign)」範式中獲得的，該範式可以追溯到公開金鑰密碼學的早期[DH76, RSA78]。

當中提到，原像可採樣函數的特性和 GPV 簽章方案也被用於為幾個（最壞情況）晶格問題提供具有高效證明者的 非互動式統計零知識證明 [PV08]。

• 公鑰和私鑰分別是 m 維晶格 L 的一個「困難」的公開描述和其陷門。

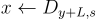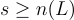• 要簽署，使用適當的公開函數將訊息雜湊到一個晶格陪集 y+L，然後使用陷門取樣一個簽章 ，這裡 是方案的一個公開參數，由用於生成陷門和取樣離散高斯的具體演算法決定。當多次簽署同一條訊息時，我們絕不應該為同一個陪集 y+L 發出多個簽章，因為這會洩露 L 中的短向量。這個問題可以通過幾種標準方法解決，要麼通過使用隨機性進行雜湊以獲得重複訊息的不同陪集，要麼通過使用狀態或偽隨機函數來獲得「可重複的隨機性」，以便我們在簽署同一條訊息時總是產生相同的簽章。
  注意，根據標準尾界 (tail bounds)，除了指數級小的概率外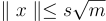

• 要驗證一條訊息上的聲稱簽章 x，將訊息雜湊以獲得陪集 y+L，並簡單檢查 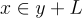和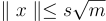

該方案的具體實例化使用 q 元 SIS 晶格 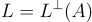和函數 ，對於均勻隨機的 作為底層的原像可採樣函數，如在上一篇所述的。

通過將公開雜湊函數建模為一個「可程式設計 (programmable)」的隨機預言機，這是雜湊並簽署範式的典型做法，我們可以證明以下非正式陳述的定理：

定理 19.1.1
假設在金鑰生成器產生的隨機晶格 LL 中（即，對於具體實例化，範數界限為 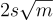的 SIS），找到範數最多為 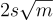的非零向量的平均情況難度，則上述方案在選擇訊息攻擊下（在隨機預言機模型中）是不可偽造的。

該定理的證明通過展示一個使用假設偽造者來在給定隨機晶格 L 中找到短向量的歸約 (reduction) 來完成。主要思想是，根據定義 5.4.3 中的統計特性，歸約可以生成正確分佈的簽章-雜湊對，而 不需要 LL 的陷門。具體來說，它可以以 正向 方向評估函數，而不是像真實方案那樣使用 反向 方向和陷門。此外，歸約可以獲得 LL 中的一個短向量，作為偽造簽章與其自身為同一條訊息內部準備的簽章之間的差值。

更詳細地說，歸約的工作原理如下：對於偽造者查詢雜湊函數 H 的每條訊息 μ（包括所有簽署查詢和最終的偽造訊息），歸約在內部選擇一個

並將雜湊函數「程式設計」為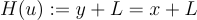
其中 y 是 x+L 的標準公開代表元。因為 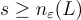。因此知道 y+L 是 L 的一個（近似）均勻隨機陪集，因此被程式設計的預言機 H 表現得像一個隨機預言機。當偽造者要求對訊息 μ 進行簽署時，歸約只需返回相應的 x，根據構造，其分佈為。

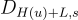與真實方案相同（在可忽略的統計誤差範圍內）。因為所有查詢都以與真實系統相同的分佈回答，偽造者最終必須以顯著概率輸出一個偽造品 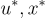。這意味著 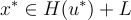且足夠短，並且偽造者從未見過歸約為 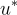內部生成的簽章 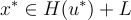，歸約只需輸出短向量 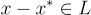，該向量以高概率非零，因為 x 的值在統計上對偽造者的視圖是隱藏的。（請注意，這種證明策略產生了一個非常「緊密 (tight)」的歸約，即歸約成功的概率幾乎與偽造者本身的成功概率完全相同。）

19.2 基於身份的加密 (Identity-Based Encryption — IBE)
將 GPV 簽章與其「對偶 (dual)」LWE 密碼系統的多使用者形式相結合，立即產生一個 基於身份的加密 (identity-based encryption — IBE) 方案。請注意，GPV 系統及其衍生物是唯一已知的被推測能抵禦量子攻擊的 IBE；其他所有 IBE 都基於二次剩餘假設（例如 [Coc01, BGH07]）或雙線性配對（例如 [BF01]）。

GPV IBE 背後的主要思想是：使用者的公鑰不再是使用者自己生成的高斯分佈私鑰 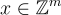和對應的公鑰 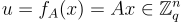，而是僅僅是使用者身份字串雜湊到 的結果，而對應的私鑰由權威機構作為對身份的 GPV 簽章生成。更詳細地說：

• 主金鑰 (master key) 是一個均勻隨機的奇偶校驗矩陣 A，主私鑰 (master secret key) 是 A 的一個陷門。此外，一個公開雜湊函數將每個使用者身份 id 映射到一個綜合徵 (syndrome)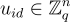
  該綜合徵作為使用者特定公鑰 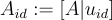的一部分。

• 要為身份 id 提取私鑰，我們使用 A 的陷門來取樣一個高斯分佈的解滿足 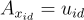即從陪集 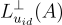上的離散高斯分佈中選擇 id。請注意，這等同於對訊息 id 簽章，並且每個身份最多應揭示一個不同的金鑰。根據在第16篇的方程式 (16.2.4)，這個 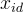可以被解釋為公鑰 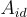的私鑰，因為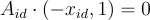

• 將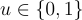
  加密到一個身份 id 以及解密完全與對偶 LWE 系統中相同（參見方程式 (5.2.5) 和 (5.2.6)），使用使用者特定的公鑰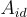
  和私鑰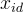

因此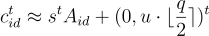

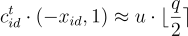
當然，對於 ℓ 位元的訊息，系統可以通過將每個身份雜湊到多個綜合徵 來以通常的方式進行分攤 (amortized)。

通過將雜湊函數建模為隨機預言機，並在適當的 LWE 假設下，上述系統可以被證明是語義安全的。（回想一下，攻擊者可以獲取它選擇的任何身份的私鑰，除了其目標身份。）證明過程或多或少與 GPV 簽章相同，甚至允許緊密歸約，儘管涉及一些與使用 LWE 相關的額外技術細節。

19.3 移除隨機預言機與分層 IBE
上述描述的簽章和 IBE 方案在其安全性分析中依賴於隨機預言機啟發式方法。Cash、Hofheinz、Kiltz 和 Peikert [CHKP10] 的一項工作給出了基於格的數位簽章和 IBE 方案，這些方案在 標準 模型（即沒有隨機預言機）中被證明是安全的，同時還有 分層 IBE (HIBE) 方案。在 HIBE 中，任何使用者都可以安全地使用其私鑰在層次結構（即樹）中將有效的私鑰 委派 (delegate) 給任何下屬使用者。我們注意到，Cash 等人的標準模型方案比其隨機預言機對應方案具有大得多的公鑰，因此不能認為是實用的。

[CHKP10] 的 HIBE 可以被視為第 5.2.2 節中對偶 LWE 密碼系統的擴展版本，其工作方式如下：考慮一個表示深度為 d 的完整二元樹的層次結構，其中樹中的每個節點自然地對應於 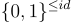中的一個字串。（這樣的樹可以通過考慮層次結構的每個層級使用幾個位元的區塊來模擬更大分支數的層次結構。）

• 主公鑰包含一個（近似）均勻隨機的矩陣 ，該矩陣生成時帶有陷門；均勻隨機的矩陣 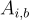，對於 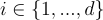和 b∈{0,1}，與 具有相同維度； 以及一個均勻隨機的伴隨量 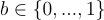，主公鑰 的陷門。

• 長度為 ℓ≤d 的身份
  對應於矩陣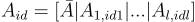
  

身份 id 的私鑰包括一個對 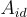，具有足夠品質的隨機陷門，以及一個高斯分佈的解 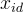滿足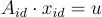

請注意，這樣的 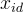，僅僅是對偶 LWE 密碼系統中公鑰 的私鑰，即 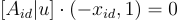，可以使用之前文章中描述的陷門抽樣、擴展和隨機化技術，從任何對id的任何前綴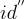

對應的 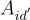具有足夠品質的陷門來生成 id 的私鑰。因此，使用者 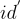可以將私鑰委派給使用者 id。（不過請記住，私鑰的品質在每次委派時會以某個多項式因子下降。）

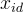• 向身份 id 的加密和解密完全與對偶 LWE 密碼系統中相同，使用公鑰 和私鑰 即密文為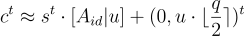

對於適當的參數選擇和 LWE 假設，上述 HIBE 系統在 選擇身份 (selective identity) 攻擊下是語義安全的。在此類攻擊中，對手必須 首先 指定目標身份 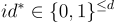，然後被給予主公鑰和一個加密給 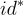的挑戰密文，並且之後可以查詢任何不是 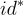前綴的身份 id 的私鑰。（通過額外的想法，可以使系統在自適應身份 (adaptive-identity) 攻擊下安全，但它變得更低效；詳見 [CHKP10]。）

安全性證明背後的主要思想如下:
設計一個歸約（一個「模擬器」），它被給予一個樣本源 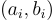，並旨在利用攻擊 HIBE 方案的敵手來確定這些樣本是 LWE 分佈的還是均勻的。模擬器首先從敵手處獲得目標身份 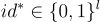，然後生成一個在 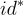處「穿孔」的主公鑰：它從足夠多的輸入樣本的
分量中組裝出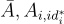

（對於 1≤i≤ℓ）和 u，並從 bi 分量中創建相應的挑戰密文。它生成所有剩餘的矩陣 Ai,b 以及秘密陷門，並將所有這些提供給敵手。現在根據構造，歸約可以為任何查詢的身份（id∗ 的前綴除外，這些查詢本來就不被允許）抽樣正確分佈的私鑰，方法是擴展和隨機化其秘密陷門。最後，請注意，如果輸入樣本是 LWE 分佈的，那麼整個模擬與真實攻擊完全匹配（達到可忽略的統計誤差），而如果它們是均勻的，則挑戰密文在資訊論上隱藏了消息。因此，歸約區分 LWE 樣本和均勻樣本的優勢本質上與 HIBE 敵手相同。

參考資料
[DH76] W. Diffie and M. E. Hellman. New directions in cryptography. IEEE Transactions on Information Theory, IT-22(6):644–654, 1976.

[RSA78] R. L. Rivest, A. Shamir, and L. M. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM, 21(2):120–126, 1978.

[Coc01] C. Cocks. An identity based encryption scheme based on quadratic residues. In IMA Int. Conf., pages 360–363. 2001

[BGH07] D. Boneh, C. Gentry, and M. Hamburg. Space-efficient identity based encryption without pairings. In FOCS, pages 647–657. 2007.

[BF01] D. Boneh and M. K. Franklin. Identity-based encryption from the Weil pairing. SIAM J.
Comput., 32(3):586–615, 2003. Preliminary version in CRYPTO 2001.

[CHKP10] D. Cash, D. Hofheinz, E. Kiltz, and C. Peikert. Bonsai trees, or how to delegate a lattice basis. J. Cryptology, 25(4):601–639, 2012. Preliminary version in Eurocrypt 2010.

[PV08] C. Peikert and V. Vaikuntanathan. Noninteractive statistical zero-knowledge proofs for lattice problems. In CRYPTO, pages 536–553. 2008.