無需陷門的數字簽署
另一條關於基於格的數字簽名的研究路線 [LM08, Lyu08, Lyu09, Lyu12, DDLL13] 與上幾篇的描述中，陷門和基於離散高斯的方法平行發展。該路線的第一項工作 [LM08] 給出了一個基於環-SIS 問題的一次性簽名，該方案可以使用標準的樹哈希技術轉換為多次使用的方案（在標準模型中）；在下面會有更詳細的描述。以一次性簽名背後的主要思想為靈感，其餘的工作遵循以下模板：首先設計一種適當類型的公開擲幣 (public-coin)、互動式 身份識別 (identification) 協議，然後應用 Fiat-Shamir 啟發式方法 [FS86] 將其轉換為隨機預言機模型中的非互動式簽名方案。回想一下，Fiat-Shamir 啟發式方法是一種通用轉換，它用隨機預言機在協議迄今為止的記錄 (transcript) 上的輸出取代了驗證者的隨機挑戰。有關此方法的更多細節在下面簡單地講解。

20.1 一次性與基於樹的簽名
Lyubashevsky 和 Micciancio [LM08] 從環-SIS 構造了一個漸近擬最優 (quasi-optimal) 的一次性簽名。這裡「擬最優」意味著對於在標準假設下推測的 λ 位元安全性（即已知的最佳攻擊需要 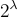時間），密鑰大小、消息長度、簽名長度以及密鑰生成、簽署和驗證的運行時間在安全參數 λ 內都是擬線性

因為該方案是擬最優的，特別是消息是 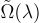位元，所以一次性簽名可以通過標準的樹哈希技術轉換為多次使用的簽名（在標準模型中），僅有對數多項式的開銷。然而，產生的多次使用方案需要一個 有狀態的 (stateful) 簽署者，並且具體的對數多項式因子似乎使該方案在實踐中不現實。

回想一下，如果攻擊者最多獲得一次其選擇消息的簽名，一次性簽名方案仍然保持不可偽造性，但如果敵手在同一密鑰下獲得超過一個簽名，則可能不提供任何安全性。
[LM08] 的完整版還包括基於標準 SIS 和編碼問題的構造，但這些不是擬最優的。

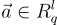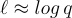為簡單起見，描述基於在 Z 上的度數為 n 的環 R 的 R-SIS 的原始一次性簽名背後的主要思想。公共參數（可以是所有使用者共享的可信隨機性）是一個奇偶校驗向量 ，其中 私鑰是兩個短的環元素向量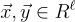

公鑰是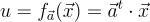

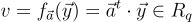
要簽署一條消息，它被解釋為一個短的環元素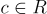
，簽名是 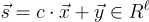要驗證，需檢查 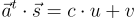且 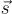足夠短。請注意，對於正確生成的簽名，驗證方程式是滿足的，因為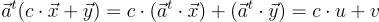

一次性安全性背後的主要思想如下：模擬器被給予 作為環-SIS 挑戰，並希望找到一個短的解 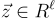，滿足 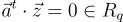，模擬器選擇自己的私鑰 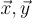並將對應的公鑰 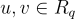給予攻擊者。因為模擬器知道私鑰，它可以簽署攻擊者選擇的任何（短）
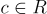產生簽名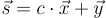
假設攻擊者隨後為一個不同的（短）c′≠c 產生了一個偽造品 。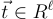

那麼有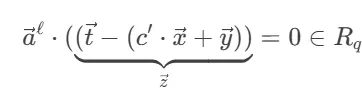

因此 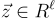是環-SIS 挑戰的一個短解，前提是它是非零的。可以證明，這種情況以顯著概率發生，因為一些關於 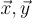的重要資訊被那一個簽名 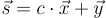隱藏了。
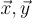（如果 在 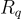上是 均勻 的，這顯然是成立的，但它們是短的，所以論證更加微妙。）由此得出，偽造者無法可靠地猜測 任何 短 c′≠c的 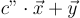的值，因此 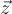以顯著概率是非零的。

20.2 身份識別協議與 Fiat-Shamir 簽名
類 Schnorr 身份識別協議:
Lyubashevsky [Lyu08] 給出了第一個基於（環）SIS 的三消息身份識別方案，該方案具有對抗主動冒充攻擊 (active impersonation attacks) 的安全性。該協議的靈感來自 Schnorr 的證明離散對數知識的協議 [Sch89]，但由於使用 短 密鑰而涉及更多的技術細節。

證明者 (prover) 有一個秘密的「非常短」的均勻隨機整數向量 ，其公鑰是 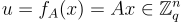，其中均勻隨機矩陣 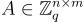，可以是由可信方生成的公共參數。協議的一次運行過程如下：

1. 證明者首先均勻隨機選擇一個「有點短」的 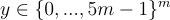並將 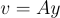發送給驗證者 (verifier)。

2. 驗證者選擇一個均勻隨機的挑戰位元 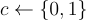，並將其發送給證明者。

3. 證明者響應如下：如果 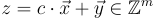是「安全的 (safe)」，即如果 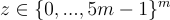則證明者將 z 發送給驗證者。否則，它中止，驗證者拒絕此次互動。

4. 如果證明者確實發送了某個 z，驗證者接受當且僅當 且 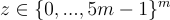否則拒絕。（請注意，合法的證明者確實能說服驗證者，因為 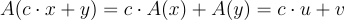符合要求。）

在完整協議中，協議的許多實例並行運行，並且僅當足夠大比例的次協議被接受時，驗證者才接受整個互動。

請注意，如果證明者沒有檢查 z 的安全性，那麼被動竊聽者可以在查看足夠多的互動後得知私鑰：如果 z 的某個條目是零（分別是 5m），則私鑰 x 的相應條目是零（分別是一）。「有點短」的定義域大小被設置得足夠大，使得 z 以某個常數概率是安全的，因此證明者不會過於頻繁地中止。使用安全性檢查，Lyubashevsky 證明該協議是（統計上）見證不可區分 (witness indistinguishable, WI) 的：無論證明者對其公鑰 u 擁有哪個私鑰 x，與證明者的互動分佈是相同的，達到極小的統計誤差。由於 WI 在平行重複下是封閉的，整個協議也保持 WI。這是基於 SIS 假設的安全性證明的關鍵事實：模擬器可以選擇自己的私鑰並充當證明者，不洩露它正在使用眾多有效私鑰中的哪一個。此外，如果敵手成功冒充證明者，通過回繞 (rewinding) 它，可以從中提取出一個有效的私鑰。根據 WI 性質，以良好的概率提取的私鑰必須與模擬器的私鑰不同，並且它們的不同是對 A 的 SIS 解決方案。

環設定中的效率
上述完整協議在通信和運行時間上效率非常低，因為需要許多並行執行來實現完備性 (completeness) 和安全性。Lyubashevsky [Lyu09] 的一項後續工作在環設定中顯著提高了這些效率度量，使用了環-SIS 函數 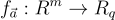定義為 （方程式 (20.2.1)）。
主要思想是將挑戰 c 的定義域從 {0,1} 擴展到 R 中所有足夠短的元素，這些元素有多個的指數級。這個版本的協議是 Schnorr 原始身份識別協議的更接近的類比。因為 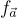是 R-線性的，很容易檢查所有驗證方程式都按要求成立，並且對於各種短對象的適當界限和適當的安全性測試，可以獲得類似的安全性證明。使用幾項額外的優化，通過將 Fiat-Shamir 啟發式方法應用於 Lyubashevsky 的協議獲得的簽名方案更接近實用：例如，對於估計約 80 位元的安全級別，簽名大小約為 60 千位元。

回歸 SIS 與進一步改進
Lyubashevsky [Lyu12] 的一項後續工作表明，要獲得具有良好通信複雜度的身份識別協議，SIS 本身實際上是足夠的（儘管環-SIS 對於獲得實用的密鑰大小和運行時間仍然很重要）。這項工作還包括各種改進，將短對象的範數減小了小的多項式因子（大約 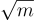），這產生了更好的具體參數，並通過更緊密的最壞情況近似因子實現了更溫和的假設。

基本思想是，證明者的私鑰現在是一個短的整數矩陣 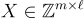其公鑰是 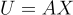協議的一次運行如下：

1.證明者從某個分佈中選擇一個「有點短」的整數向量 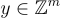，並將 v = Ay 發送給驗證者。

2. 驗證者選擇一個短的挑戰向量 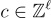，證明者計算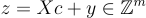

3. 證明者然後對 z 應用一個適當的拒絕規則，要麼將其發送給驗證者，要麼中止。

4. 如果證明者確實發送了某個 z，驗證者檢查 Az=Uc+v 且 z 足夠短。請注意，合法的證明者確實能說服驗證者，因為 Az=A(Xc+y)=Uc+v。

對於合理的參數，只需要協議的小常數次並行運行即可建立足夠的完備性和安全性。

與先前使用對 z 進行非全即無「安全性檢查」的工作不同，這裡的拒絕規則是一種更精細的 概率性 測試，基於拒絕抽樣 (rejection sampling)。本質上，目標是確保 在未拒絕條件下 的 z=Xc+y 的分佈獨立於 X。這是通過使用拒絕抽樣來「重新居中 (recenter)」 z 的分佈為以零為中心的離散高斯分佈，而不是以 Xc 為中心來實現的。為了確保 z 不會過於頻繁地被拒絕，讓 y 具有一個離散高斯分佈，其參數與（||Xc ||的上界）成正比。這確保了以零為中心和以 Xc 為中心的離散高斯分佈有足夠的重疊。這個想法的進一步改進使用了「雙峰 (bimodal)」高斯分佈 [DDLL13]，本質上是通過讓證明者在 ±Xc 之間隨機選擇。這產生了稍微更多的重疊，並允許將 y 的高斯參數減少大約一個 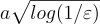因子（對於統計距離 ε）。

實踐:
使用幾項額外的優化和工程技巧，[GLP12] 中提出了一個使用單峰高斯分佈方案的現場可程式設計閘陣列 (FPGA) 實作。對於估計約 80 位元的安全級別，其公鑰和私鑰分別約為 12 和 2 千位元，簽名約為 9 千位元。一個基於環的雙峰方案的軟體實作，稱為 BLISS，也在 [DDLL13] 中給出。對於估計 128 位元的安全級別，其公鑰和私鑰分別約為 7 和 2 千位元，簽名約為 5.6 千位元。簽署和驗證時間與 RSA-2048 相比具有競爭力。

參考資料
[LM08] V. Lyubashevsky and D. Micciancio. Asymptotically efficient lattice-based digital signatures. In TCC, pages 37–54. 2008.

[Lyu08] V. Lyubashevsky. Lattice-based identification schemes secure under active attacks. In Public Key Cryptography, pages 162–179. 2008.

[Lyu09] V. Lyubashevsky. Fiat-Shamir with aborts: Applications to lattice and factoring-based signatures. In ASIACRYPT, pages 598–616. 2009.

[Lyu12] V. Lyubashevsky. Lattice signatures without trapdoors. In EUROCRYPT, pages 738–755. 2012.

[DDLL13] L. Ducas, A. Durmus, T. Lepoint, and V. Lyubashevsky. Lattice signatures and bimodal gaussians. In CRYPTO, pages 40–56. 2013.

[FS86] A. Fiat and A. Shamir. How to prove yourself: Practical solutions to identification and signature problems. In CRYPTO, pages 186–194. 1986.

[Sch89] C. Schnorr. Efficient signature generation by smart cards. J. Cryptology, 4(3):161–174, 1991. Preliminary version in CRYPTO 1989.

[GLP12] T. Guneysu, V. Lyubashevsky, and T. P ¨ oppelmann. Practical lattice-based cryptography: A signature scheme for embedded systems. In CHES, pages 530–547. 2012.