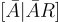接著上一篇的講解，對於某個足夠短的隨機矩陣 R。與往常一樣，語義安全性遵循一個不可逆性論證 (lossiness argument)：在一個均勻隨機的（「畸形的」）公鑰 (Public Key) 下進行加密會在統計上隱藏消息，因為 非常接近均勻分佈。

要使用秘密金鑰 s 解密密文 A，只需計算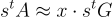
，

其中的近似關係由方程式 (23.1.7) 成立，並且因為 R 是短的。由於很容易求解關於 G 的 LWE 問題，可以恢復 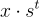，從而恢復 x（模 q）。事實上，如果已知 x 只是一個位元，那麼因為 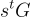的最右邊的一個條目模 q 遠離零，可以簡單地測試 A 的某個適當列 a 是否滿足 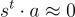來恢復 x。

要對加密了小消息的密文 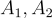進行同態加法或乘法，只需分別計算 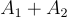或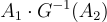
如上方的方程式 (23.1.5) 和 (23.1.6) 所示，得到的密文分別是對消息之和或乘積的有效加密。因為為了控制雜訊增長，保持消息為小整數至關重要，所以通常只使用能將消息維持在 {0,1} 值的操作。例如，足以表達任意計算的二元 NAND 操作可以寫為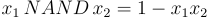

24.1 自舉 (Bootstrapping):
正如 Brakerski 和 Vaikuntanathan [BV14] 首次所示，陷門矩陣在同態乘法下所呈現的非對稱且擬加性的 (asymmetric and quasi-additive) 增長特性，允許以相當小的誤差增長來執行某些計算 — — 特別是為了自舉目的而進行的解密計算。第一個主要觀察結果是，根據方程式 (23.1.6)，對新鮮密文進行的任何多項式長度的同態位元乘法鏈，如果以右結合 (right-associative) 的方式進行，只會引起多項式的誤差增長。當乘以一系列置換 (permutation) 矩陣（或更一般地說，正交整數矩陣）時，同樣成立，其中每個矩陣都是按条目加密的。

第二個主要想法是，通過使用 Barrington 定理 [Bar86]，任何深度為 d 的電路都可以轉換為一個長度為 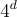，由置換矩陣組成的分支程式 (branching program)。特別是，深度為 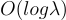的解密電路可以在多項式時間內並以多項式誤差增長進行同態計算，儘管這裡的多項式係數相當大。後續 Alperin-Sheriff 和 Peikert [AP14] 的工作透過避免使用 Barrington 定理，轉而將解密表示為一個可以直接嵌入到置換矩陣中的算術函數，從而顯著將運行時間和誤差增長改進為較小的多項式。Ducas 和 Micciancio [DM15] 設計並實現了此方法的一個版本，其中融合了更多想法，產生了一個在標準桌面硬體上能在不到一秒的時間內評估一個完整「自舉 NAND 閘」的系統。

24.2 全同態簽章 (Fully homomorphic signatures):
Gorbunov、Vaikuntanathan 和 Wichs [GVW15b] 展示了同態陷門如何也能用於實現全同態簽章 (FHS)。FHS 的精確定義模型和安全目標超出了本調查報告的範圍，但其基本思想如下：簽署者使用其公鑰對一些初始資料 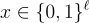進行簽署，產生一個簽章 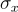。然後，僅給定公鑰、x 和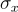

一個不可信的運算者可以對 x 應用任意函數 f，並為值 y=f(x) 計算出對應的簽章 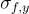，驗證者僅給定公鑰、f、y 和 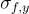，但沒有 x 本身，可以驗證 y 確實是簽署者最初簽署的某個資料 x 經函數 f 計算後的值。

全同態簽章相當自然地從上述同態陷門中產生。公鑰是一個均勻隨機的 連同另外 ℓ 個均勻隨機的矩陣
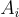
每個矩陣對應資料 x 的一個位元的待簽署的原始資料。秘密金鑰是 的一個陷門。要對資料 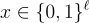進行簽署，簽署者使用陷門來抽樣一個滿足 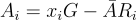的高斯分佈 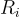而簽章就是所有這些 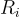的集合。

簽章上的同態操作以及簽章驗證定義如下。
對於任何謂詞 (predicate) 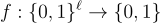，不失一般性地表示為加法與乘法閘的算術電路，遞迴地定義一個矩陣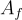
其計算方式如下：

• 如果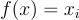
  （對於某個 i），則定義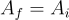

• 如果 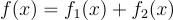對於某個謂詞 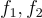，則令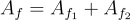

• 否則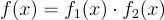
  對於某個謂詞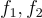

令 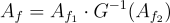給定某個 x 及其對應的簽章分量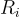
要同態推導出一個證明 f(x)=y（對於某個謂詞 f）的簽章，只需計算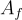
，並透過方程式 (23.1.5) 和 (23.1.6) 得到一個滿足 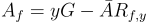的短矩陣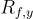

驗證者同樣可以僅從 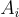和 f（無需知道 x）計算出 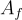並且可以驗證所提交的 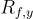是否足夠短並且滿足上述關係。

參考資料
[BV14] Z. Brakerski and V. Vaikuntanathan. Lattice-based FHE as secure as PKE. In ITCS, pages 1–12. 2014.

[Bar86] D. A. M. Barrington. Bounded-width polynomial-size branching programs recognize exactly those languages in NC1 . In STOC, pages 1–5. 1986.

[AP14] J. Alperin-Sheriff and C. Peikert. Faster bootstrapping with polynomial error. In CRYPTO, pages 297–314. 2014.

[DM15] L. Ducas and D. Micciancio. FHEW: Bootstrapping homomorphic encryption in less than a
second. In EUROCRYPT, pages 617–640. 2015.

[GVW15b] S. Gorbunov, V. Vaikuntanathan, and D. Wichs. Leveled fully homomorphic signatures from standard lattices. In STOC, pages 469–477. 2015.