Day 22. ADT-Algebraic Data Type

17th鐵人賽 magma semigroup monoid group

olddunk

2025-09-22 08:54:38

62 瀏覽

分享至

Algebraic Data Type

現代代數最重要的工作便是將一些代數性質抽象化，而代數中最重要的就是運算，我們今天就要討論運算抽象化這個主題。數字中最常使用的兩種運算是加法和乘法，而加法和乘法的本質都是二元運算，而且大部分的性質皆相同，都滿足封閉性、結合律、運算單位元素，最大的不同是運算反元素的存在性(加法必然有反元素，而0在乘法中沒有反元素)。封閉性、結合律、運算單位元素和運算反元素的觀念並不是只能用於數字，以字串而言，加法的運用是很直覺，字串abc加字串def便可得到字串abcdef。布林值運算的or可以扮演數字的加法，乘法則由and扮演。今天就依這些性質建立不同的類別，這些類別我們稱之為ADT(Algebraic Data Type)。

Magma - 封閉性

第一個要介紹的是封閉性。在數學上，二元運算也是函數，可以視為二個參數的函數。而研究二元運算的第一個要點便是封閉性，也就是說回傳的結果是否仍屬於定義域。以typescript的函數來說便是兩個型別A的參數，它的回傳型別仍然是型別A，而滿足這個性質的類別介面便稱為Magma<A>，它的定義如下：

export interface Magma<A> {
  readonly concat: (x: A, y: A) => A
}

也就是說，只要能替型別A建立一個具有concat方法的物件，型別A便是屬於類別Magma。函數取名為concat是取其連接的意義，數字上的加法、乘法和減法都滿足這個要求，其實任何運算滿足封閉性便可稱為concat。

Semigroup - 結合律

封閉性的滿足並不困難，我們很少直接使用Magma類別。如果一個運算另外還滿足了結合律，我們便稱其為「半群」(Semigroup)，假設我們的運算符號是*，運算的結合律便是(a * b) * c = a * (b * c)，因為計算的次序不重要，括號便可省略不寫。一個運算是否滿足結合律，typescript的型別處理幫不上忙，我們必須自行檢查。結合律是一個運算式可以平行運的基礎，a + b + c + d + e + f + g + h = (a + b) + (c + d) + (e + f) + (g + h)的括號內計算時，互不影響。Semigroup的型別定義和Magma完全一樣，由於Semigroup滿餐了結合律，fp-ts的Semigroup模組另外提供了concatAll函數，讓我們可以一次將陣列中所有的元素一起concat，concatAll的HM型別簽名如下：

concatAll :: Semigroup a => a => [a] => a

型別A必須是Semigroup類別，所以第1個參數是Semigroup實例(一個有concat方法的物件)，第2個參數是型別A的運算初始值，第3個參數是型別A的陣列，最後回傳一個型別A的結果。

import * as S from 'fp-ts/Semigroup'
import * as N from 'fp-ts/number'

const sum = S.concatAll(N.SemigroupSum)(2) // 2是起始值

console.log(sum([1, 2, 3, 4])) // => 12

const product = S.concatAll(N.SemigroupProduct)(3)

console.log(product([1, 2, 3, 4])) // => 72

以下是一些在fp-ts在各模組已實作的Semigroup實例：

fp-ts/number: SemigroupProduct, SemigroupSum
fp-ts/string: Semigroup
fp-ts/boolean: SemigroupAll, SemigroupAny

除了這些我們在數學上常見的實例，我們再看一些其它的Semigroup。

import { Semigroup } from 'fp-ts/Semigroup';
/** 一個對任何型別都成立的半群，可以傳回第一個參數 */
const semigroupGetFirst = <A = never>(): Semigroup<A> => ({
  concat: (first: A, second: A) => first,
});
/** 一個對任何型別都成立的半群，可以傳回第二個參數 */
const semigroupGetLast = <A = never>(): Semigroup<A> => ({
  concat: (first: A, second: A) => second,
});
console.log(semigroupGetFirst<number>().concat(3, 5)); // 3
console.log(semigroupGetLast<number>().concat(3, 5));  //5

Semigroup模組裏提供了max和min兩個類別實例建構函數，只要提供Ord的實例當參數便可建構Semigroup的實例。

import { Semigroup, min, max } from 'fp-ts/Semigroup';
/** 傳回兩個數之間較大者的半群 */
const semigroupMin: Semigroup<number> = min(N.Ord);

/** 傳回兩個數之間較小者的半群  */
const semigroupMax: Semigroup<number> = max(N.Ord);
console.log(semigroupMax.concat(9, 10)); // 10
console.log(semigroupMin.concat(9, 10)); // 9

我們也可以透過fp-ts/Semigroup模組中的struct函數根據物件各屬性型別的Semigroup類別實例來建構物件的Semigroup類別實例。

type Point = {
  x: number;
  y: number;
};

const semigroupPoint: Semigroup<Point> = struct({
  x: N.SemigroupSum,
  y: N.SemigroupSum,
});

console.log(semigroupPoint.concat({ x: 1, y: 4 }, { x: -3, y: 5 })); // { x: -2, y: 9 }

另外在fp-ts/function模組中有一個getSemigroup函數可以根據函數的回傳值建構函數型別的Semigroup類別實例。

import * as B from 'fp-ts/boolean';
import { getSemigroup } from 'fp-ts/function';
const semigroupPredicateAll: Semigroup<(p: Point) => boolean> = getSemigroup(
  B.SemigroupAll
)<Point>();

const isPositiveX = (p: Point): boolean => p.x > 0;
const isPositiveY = (p: Point): boolean => p.y > 0;
const isFirstQuadrant = semigroupPredicateAll.concat(isPositiveX, isPositiveY);

console.log(isFirstQuadrant({ x: 3, y: 5 })); // true

Monoid - 單位元素

任何具有單位元素的運算結構稱為Monoid，在fp-ts中Monoid<A>是具備empty屬性(型別A)的Semigroup類別介面，我們稱empty是單位元素。

0是加法的單位元素，因為任何數加0其值不變；因為任何數乘以1其值不變，同理乘法的單位元素是1；任何字串concat空字串其值也不變，字串concat的單位元素便是空字串；布林運算and的單位元素是false，or的單位元素是true，這些都是常見運算單位元素。

interface Monoid<A> extends Semigroup<A> {
  readonly empty: A
}

Monoid的操作和Semigroup差不多，由於有單位元素，因此Monoid模組中的concatAll函數不需要起始值，因此只需要型別A的Monoid實例和型別A陣列二個參數。

import { concatAll } from 'fp-ts/Monoid';
import * as N from 'fp-ts/number';
console.log(concatAll(N.MonoidProduct)([1, 2, 3, 4]));

Group - 反元素

5 + (-5) = 0，-5是5的加法反元素，任何運算反元素存在的運算結構，我們稱之為群(Group)，fp-ts中Group的定義如下：

interface Group<A> extends Monoid<A> {
  readonly inverse: (a: A) => A
}

反元素存在比較嚴格，不是每個運算結構都可以成為Group，加法在number中具有反元素，乘法則沒有，字串的concat也沒有反元素。一個運算有沒有反元素必須仔細檢查，其實Group的使用機會並不多，我們就簡單介紹它的定義。

今日小結

Magma、Semigroup、Monoid和Group的關係如下圖，通常在應用情境都會有單位元素，所以大部分時機都直接使用Monoid介面。

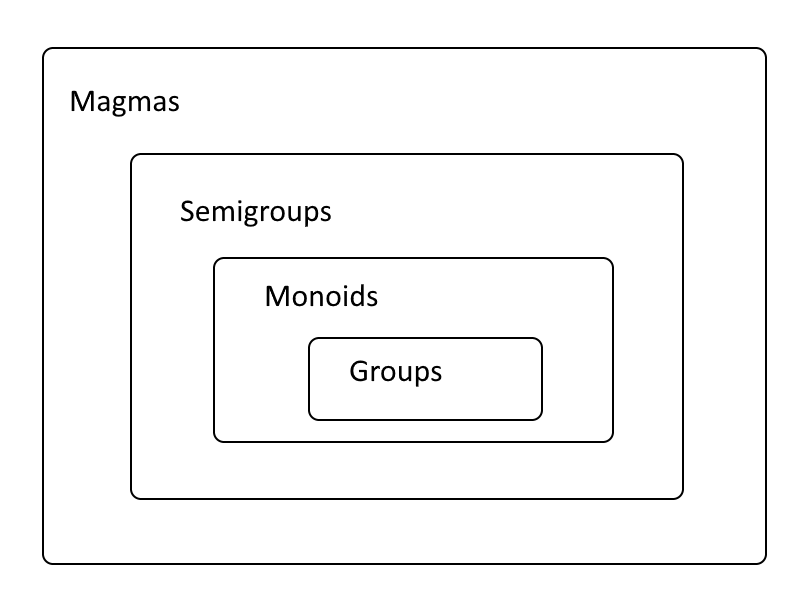
(資料來源：https://www.johndcook.com/associative.png)

今天的內容較比較偏向抽象代數，其實並不困難，我們從小就在數學課中熟悉它們代表的性質，只要了解Magma(封閉性)、Semigroup(結合律)、Monoid(運算單位元素)和Group(運算反元素)這些術語所代表的性質即可以使用這些類別。更重要的是能夠在新的運算中觀察是否滿足這些性質，進而建立它們類別實例來應用。今天的分享內容到此為止，明日再見。