題目

Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:
0 <= a, b, c, d < n
a, b, c, and d are distinct.
nums[a] + nums[b] + nums[c] + nums[d] == target
You may return the answer in any order.

Example

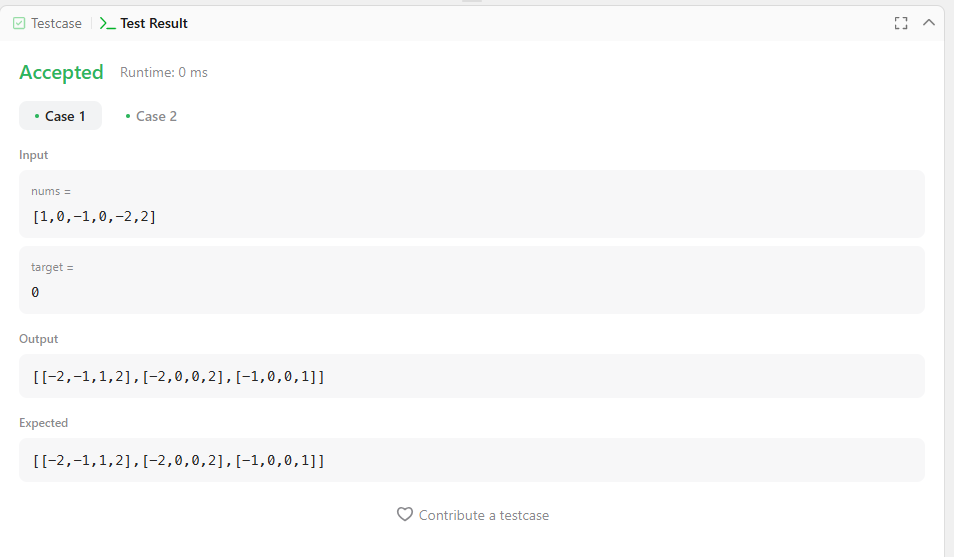
Input: nums = [1,0,-1,0,-2,2], target = 0
Output: [[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

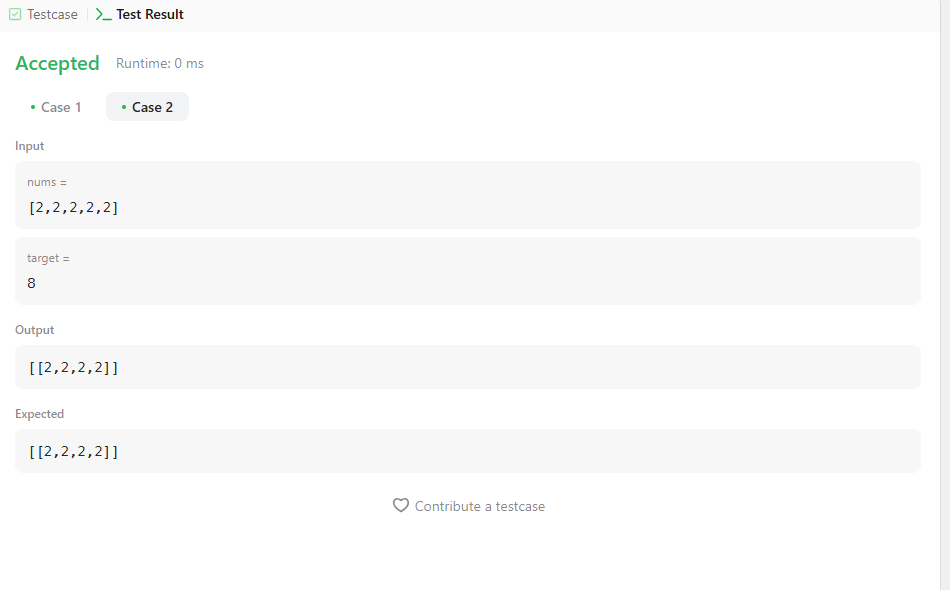
Input: nums = [2,2,2,2,2], target = 8
Output: [[2,2,2,2]]

Constraints

1 <= nums.length <= 200

-10^9 <= nums[i] <= 10^9

-10^9 <= target <= 10^9

解題思路

這題是 3Sum 的進階版，只是要找「四個數」相加等於 target。
主要思路：

先對陣列排序，方便去重與雙指針移動。

用兩層迴圈固定前兩個數字 i 和 j。

針對剩下的區間使用雙指針 left 與 right，去嘗試找到符合的組合。

如果總和等於 target，存入結果，並跳過重複數字。

如果總和小於 target，就讓 left++；如果總和大於 target，就讓 right--。

這樣的時間複雜度為 O(n^3)，在 n <= 200 時可以接受。

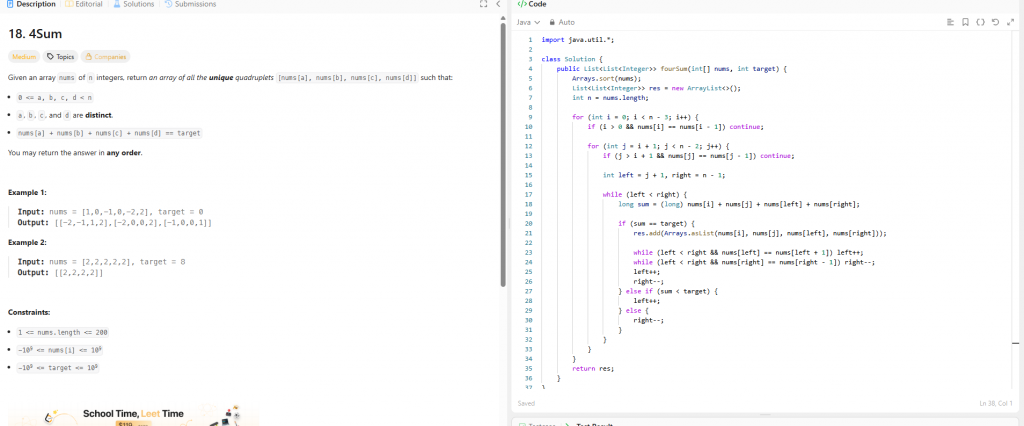
程式碼（Java）
import java.util.*;

class Solution {
public List<List> fourSum(int[] nums, int target) {
Arrays.sort(nums);
List<List> res = new ArrayList<>();
int n = nums.length;

    for (int i = 0; i < n - 3; i++) {
        if (i > 0 && nums[i] == nums[i - 1]) continue;

        for (int j = i + 1; j < n - 2; j++) {
            if (j > i + 1 && nums[j] == nums[j - 1]) continue;

            int left = j + 1, right = n - 1;

            while (left < right) {
                long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];

                if (sum == target) {
                    res.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));

                    while (left < right && nums[left] == nums[left + 1]) left++;
                    while (left < right && nums[right] == nums[right - 1]) right--;

                    left++;
                    right--;
                } else if (sum < target) {
                    left++;
                } else {
                    right--;
                }
            }
        }
    }
    return res;
}

}

心得

這題一開始看到會覺得跟 3Sum 幾乎一樣，但多一層迴圈就很容易超時。
重點是：

排序是關鍵，能讓我們用雙指針解決問題。

去重邏輯要小心，不然會產生重複解答。

大數值運算要用 long，避免溢位。