題目

給定一個包含 k 個已排序的鏈結串列的陣列，將它們合併成一個已排序的鏈結串列，並返回合併後的結果。

範例

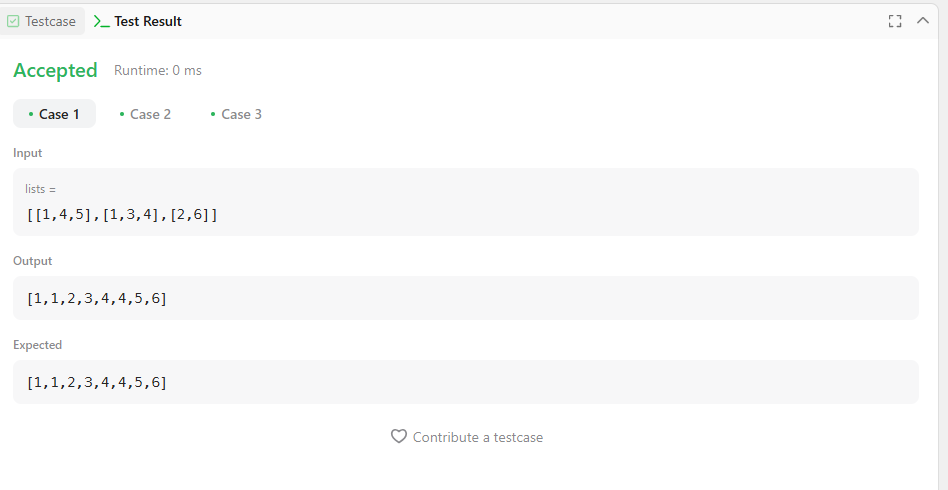
Input:
lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation:

[
1->4->5,
1->3->4,
2->6
]
合併後為：
1->1->2->3->4->4->5->6

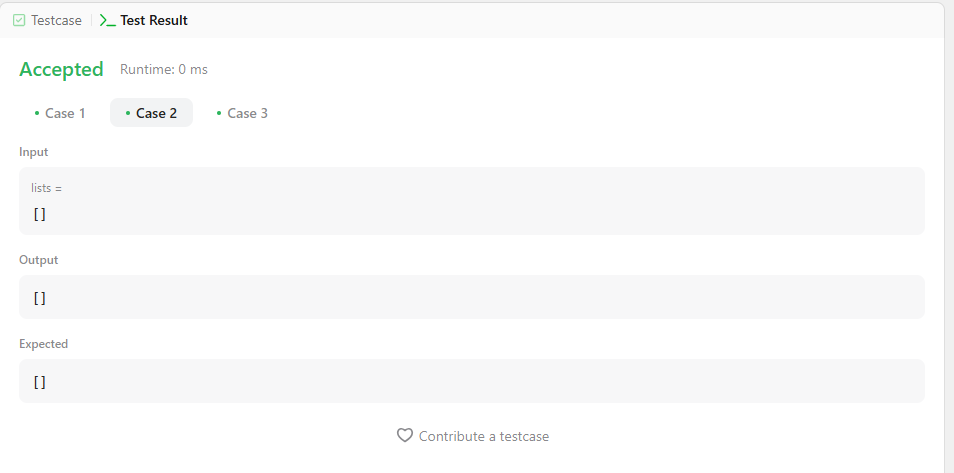
Input: lists = []
Output: []

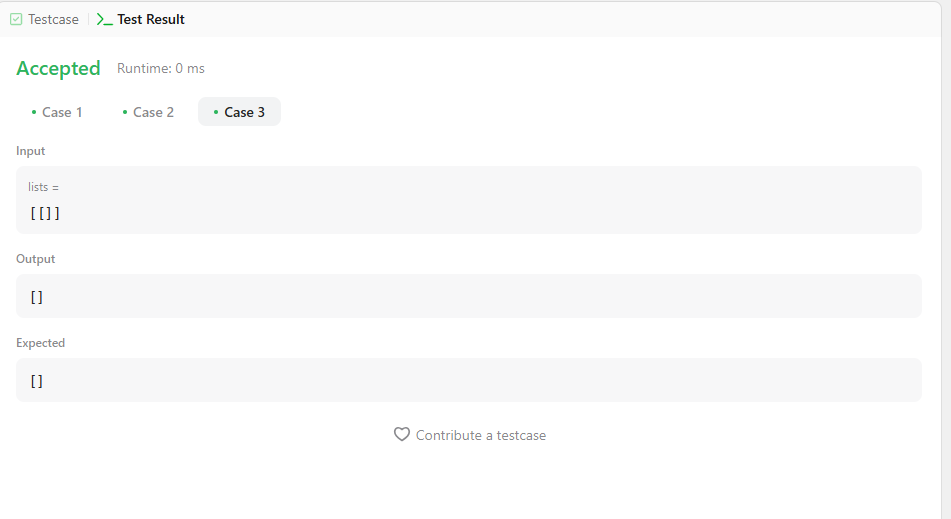
Input: lists = [[]]
Output: []

Constraints

k == lists.length

0 <= k <= 10^4

0 <= lists[i].length <= 500

-10^4 <= lists[i][j] <= 10^4

lists[i] 已排序

所有 lists[i] 的總長度不超過 10^4

解題思路

這題可以用多種方法：

線性合併：依序兩兩合併，時間複雜度高。

最小堆（Priority Queue）：同時取所有鏈表中最小的節點，時間複雜度較低，為 O(N log k)。

分治法：將 k 個列表兩兩合併，直到只剩下一個，時間複雜度 O(N log k)。

最常用的是 Priority Queue，因為簡單又高效。

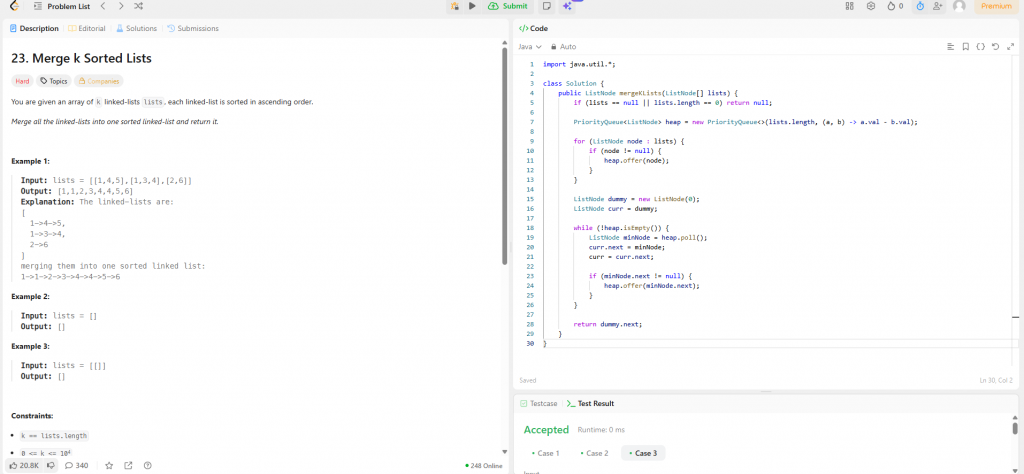
程式碼（Java）
import java.util.*;

class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists == null || lists.length == 0) return null;

    PriorityQueue<ListNode> heap = new PriorityQueue<>(lists.length, (a, b) -> a.val - b.val);

    for (ListNode node : lists) {
        if (node != null) {
            heap.offer(node);
        }
    }

    ListNode dummy = new ListNode(0);
    ListNode curr = dummy;

    while (!heap.isEmpty()) {
        ListNode minNode = heap.poll();
        curr.next = minNode;
        curr = curr.next;

        if (minNode.next != null) {
            heap.offer(minNode.next);
        }
    }

    return dummy.next;
}

}

心得

這題是 Priority Queue + LinkedList 的經典題目，非常適合練習「堆疊資料結構」的運用。
透過最小堆，我們可以保證每一步都取到最小節點，保持整個列表的有序性。
時間複雜度是 O(N log k)，其中 N 是所有鏈表的總節點數，k 是鏈表數量。

這題在實際工程中很常遇到，例如合併多個已排序的資料流。
對我來說，Priority Queue 的寫法是最快且穩定的解法。