題目

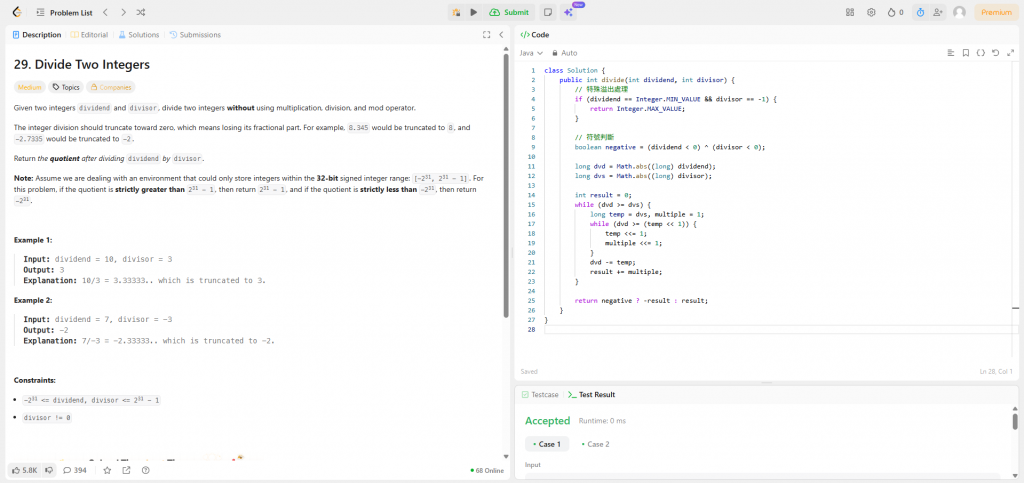
給定兩個整數 dividend 和 divisor，要求 不使用乘法、除法和 mod 運算，實現兩個整數的除法。
結果需要向零截斷（丟掉小數部分）。

注意：

假設運行環境能存儲的整數範圍為 32 位有符號整數: [−2³¹, 2³¹ − 1]。

如果結果超出範圍，則返回範圍內的最大/最小值。

範例

Input: dividend = 10, divisor = 3
Output: 3
Explanation: 10 / 3 = 3.333... 截斷後為 3。

Input: dividend = 7, divisor = -3
Output: -2
Explanation: 7 / (-3) = -2.333... 截斷後為 -2。

解題思路

由於不能用乘除模，我們可以用 位移運算 (bit shifting) 來達成加速除法。
核心想法：

將除數一直左移（相當於乘 2）直到大於被除數。

從最大的左移量開始，減去被除數並累加結果。

注意處理符號，最後返回帶符號的結果。

特殊情況：溢出（Integer.MIN_VALUE / -1）。

時間複雜度：O(log N)。

Java 實作
class Solution {
public int divide(int dividend, int divisor) {
// 特殊溢出處理
if (dividend == Integer.MIN_VALUE && divisor == -1) {
return Integer.MAX_VALUE;
}

    // 符號判斷
    boolean negative = (dividend < 0) ^ (divisor < 0);

    long dvd = Math.abs((long) dividend);
    long dvs = Math.abs((long) divisor);

    int result = 0;
    while (dvd >= dvs) {
        long temp = dvs, multiple = 1;
        while (dvd >= (temp << 1)) {
            temp <<= 1;
            multiple <<= 1;
        }
        dvd -= temp;
        result += multiple;
    }

    return negative ? -result : result;
}

}

心得

這題讓我學到 位運算在數學運算中的應用，特別是用左移取代乘法，右移取代除法，能大幅提升效率。
此外，處理溢出與符號也是考驗邏輯的部分。
雖然 LeetCode 上有直接的除法方法，但遵循題目限制能讓我更了解底層的數學運算原理。