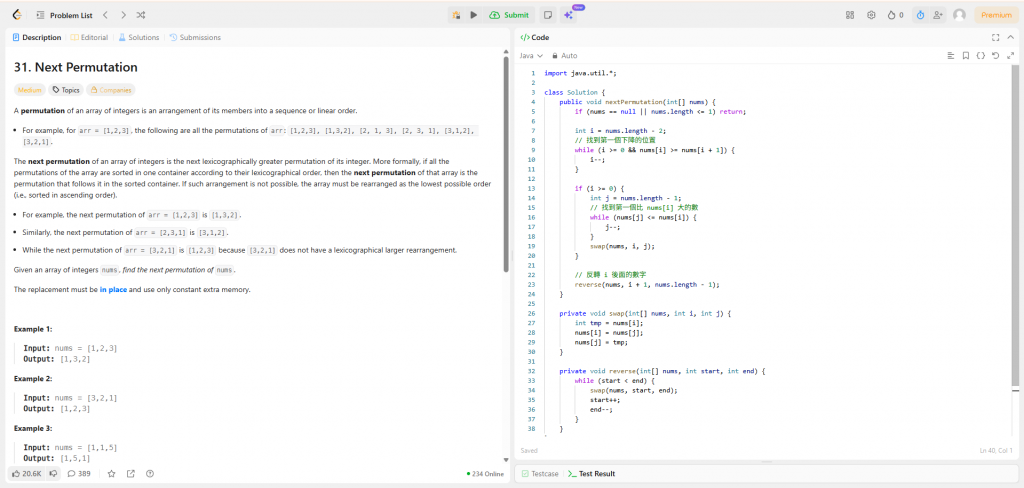
題目

給定一個整數陣列 nums，找出它的 下一個排列（lexicographically larger permutation）。
如果不存在更大的排列，則將它重新排列為 最小排列（升序排列）。
必須 就地修改 並且使用 常數額外空間。

範例

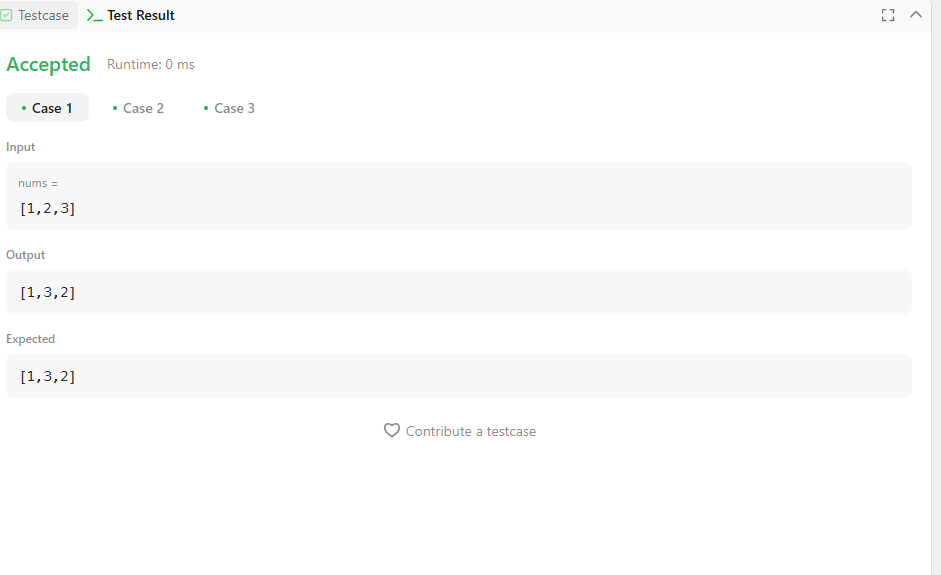
Input: nums = [1,2,3]
Output: [1,3,2]

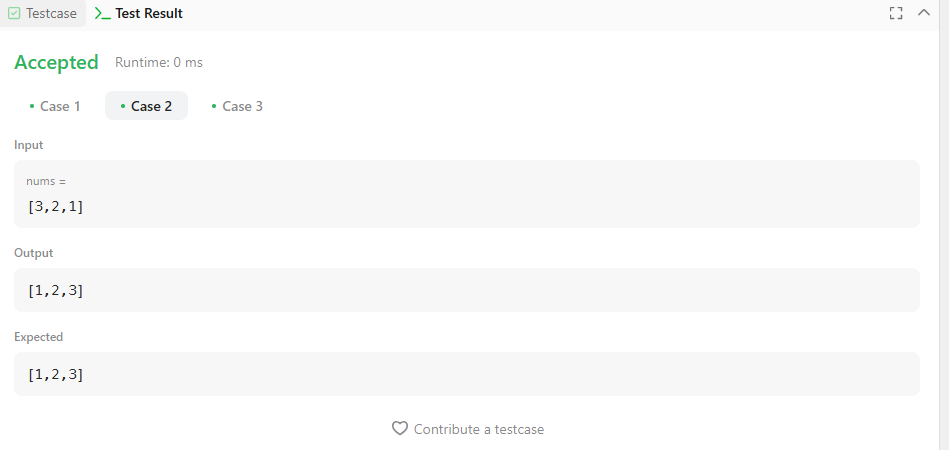
Input: nums = [3,2,1]
Output: [1,2,3]

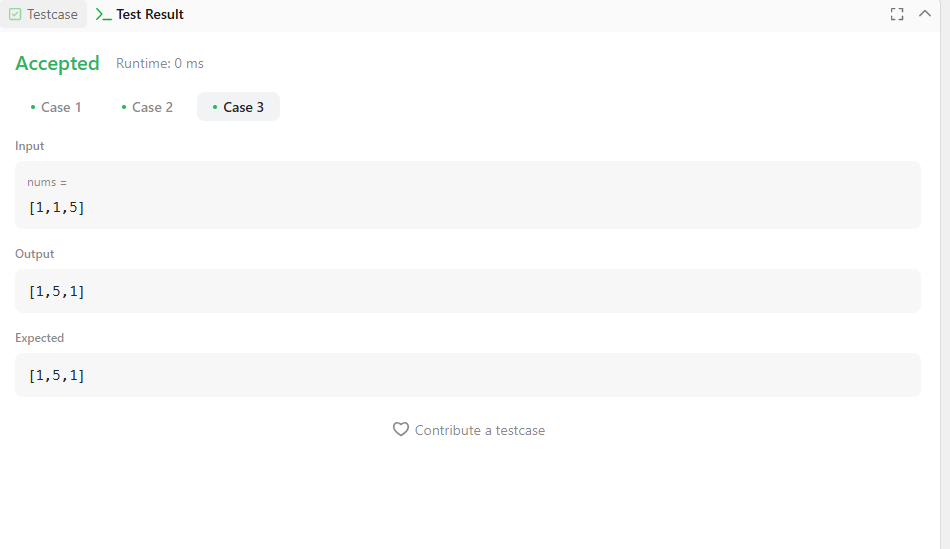
Input: nums = [1,1,5]
Output: [1,5,1]

解題思路

這題是一個經典的排列生成問題，可以用以下步驟解決：

從右往左找到第一個 nums[i] < nums[i+1] 的位置 i，這表示從 i 後面的部分已經是遞減排列，需做調整。

從右往左找到第一個大於 nums[i] 的元素位置 j。

交換 nums[i] 與 nums[j]。

將 i 後面的部分反轉，變成最小排列。

這樣就能得到下一個字典序排列。

時間複雜度：O(n)，空間複雜度：O(1)。

Java 實作
import java.util.*;

class Solution {
public void nextPermutation(int[] nums) {
if (nums == null || nums.length <= 1) return;

    int i = nums.length - 2;
    // 找到第一個下降的位置
    while (i >= 0 && nums[i] >= nums[i + 1]) {
        i--;
    }

    if (i >= 0) {
        int j = nums.length - 1;
        // 找到第一個比 nums[i] 大的數
        while (nums[j] <= nums[i]) {
            j--;
        }
        swap(nums, i, j);
    }

    // 反轉 i 後面的數字
    reverse(nums, i + 1, nums.length - 1);
}

private void swap(int[] nums, int i, int j) {
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}

private void reverse(int[] nums, int start, int end) {
    while (start < end) {
        swap(nums, start, end);
        start++;
        end--;
    }
}

}

心得

這題看似複雜，但其實就是一步步找到下一個排列的規則。
關鍵在於理解 字典序 和如何透過交換及反轉達成下一個排列。
這種題型非常實用，特別在排列組合或搜尋優化的問題上。