不好意思拉~~我專有名詞通常都是用英文，我覺得這樣比較原汁原味，看不懂英文也沒有關係，我其實都會稍微解釋，如果還聽不懂的話就發問吧！

前面我們提到了很多的regression，而也提到的機器學習當中一個重要的議題，也就是overfitting。
那是怎麼一回事呢，我們來看下面這張圖。

我們會期待一個好的模型會學到像左邊的樣子，但是當模型太強大了，為了符合跟資料的error最小，所以他就會扭的亂七八糟的像右邊那樣，而這不是我們想要的，這就是overfitting。

這就像讓小朋友考試一樣，拿了試題給小朋友做，小朋友做的滾瓜爛熟，但是一旦上考場確只會寫試題中有的類似題目，其他的綜合應用題卻不會了。

面對overfitting，我們有可以跟他對抗的方法，就是regularization，他就是在loss function上加上一些額外的分數用來防止整個model變得太奇怪。

ridge regression

我們先介紹的ridge regression，他就是regression加上L2 norm的regularization。
我舉個例子，像是polynomial regression是個非常容易overfitting的模型，因為當你的資料看起來比較像拋物線的形狀，但是卻假設了二次以上的多項式去學習，這麼一來就容易變成很高次多項式了。

這時候我們會想要避免模型複雜度太高，也就是跑到太高次去。
我們會加入以下的項

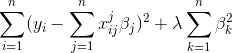
前面的部份是polynomial regression的least square，我們在後面加了一項係數的平方和，他會產生的一個效果是，當很多項的係數不為0的時候就會連同一起被計算進loss function中，所以就加重了對模型複雜度的限制。

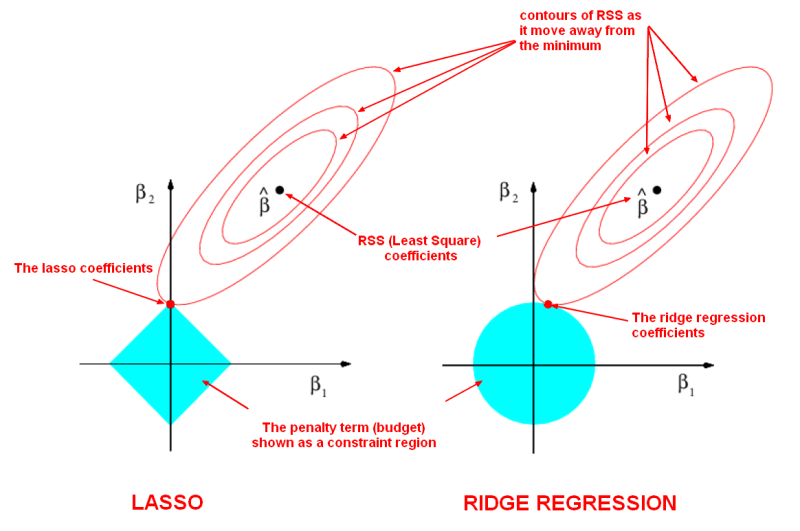
那把loss function畫出來看的話就像是，我們在的點是原點，正在一步一步前往最低點，regularization就像是在我們外圍包了一層防護罩，提早碰到防護罩就提早停止。

lasso regression

後來有人提出了用L1 norm來做regularization。
他跟L2 norm最大的不同就是一個是平方一個是用絕對值，而L1 norm的效果是讓一些不重要或是影響較小的變數係數為0，如此一來就可以同步達到篩選特徵的效果。

當特徵減少，用來預測的準確度就可以比較穩定，而解釋上也比較容易。
L1 norm畫出來就像個菱形。

elastic net regression

ElasticNet是個神奇的版本，他融合了以上L1跟L2 norm，所以他擁有了篩選特徵跟降低模型複雜度的效果，但是要在兩者間權衡到底要用哪個比較多，或是一樣多。