Bayesian statistics有什麼應用呢？
就是Naive Bayes classifier拉~~~

其前面那個naive我一直不知道要怎麼翻他，有的翻成單純、簡單、樸素等等，那就自己挑一個喜歡的吧XD

重新定義公式

前面我們談過貝式定理，那他怎麼使用到機器學習的運算上來呢？
我們把公式用另一個方式解釋

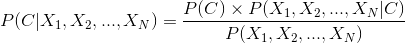
通常分類問題指的是我的資料有他的特徵（X1, X2, ..., XN）跟他的分類C，所以我們可以把貝式定理套用到這邊來，就變成了以上的樣子。

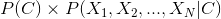
但是實際上我們關心的是分子的部份，分母其實只要在輸出的時候做一次的轉換即可。

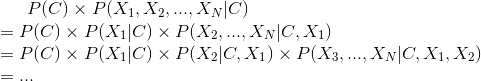
進行計算的時候我們必須提供的資訊實在很多，當他一展開之後就是驚人的運算量。

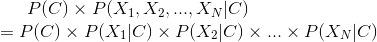
幸好是，我們可以假設特徵跟特徵之間是（統計）獨立的，也就是獨立事件、各自獨立、沒關係的！
所以式子就會被簡化成以上這樣。

Pseudo-code

以上的式子看不懂嗎？沒關係！我們把他化成pseudo-code！

其實我們還有一件事情沒有決定，也就是特徵的分佈的樣子是什麼，前面我們假設從袋子中抽出球會呈現二項式分布，那這邊我們通常會假設特徵是呈現常態分佈的。

如果連結回我們前面的機器學習框架的話，模型應該是貝式定理，error應該是呈現常態分佈，最佳化的方法是Maximum likelihood estimation (MLE)，不過我們這邊沒有講。

由於MLE不是我們這篇的重點，我先講結論，前面的方法中我們將loss function套入最佳化演算法中，最佳化的目的是找到一組最好的參數，這樣就知道訓練好的模型長什麼樣子。
然而對常態分佈來說，需要決定的參數就是平均數跟標準差了！而且剛好常態分佈的error配上MLE，平均值跟標準差的計算就如同我們高中背的公式那樣！
所以我們就可以省略MLE的煩雜計算了。

先假設我們的分類有3類好了，N個特徵

prob = 初始化為一個空矩陣
C = 初始化為一個空向量
for i=1...3
    for j=1...N
        mean, sd = 拿i類的資料，計算j的平均及標準差
        prob[i, j] = (mean, sd)  # 存起來，之後推論的時候要用
    end
    C[i] = 計算i類佔全部的比例
end

以上是training的部份。

假設要預測(X1, X2, ..., XN)被分在哪一類

X = 要預測的資料特徵
prob_C = 初始化為空向量
for i=1...3
    p = 1
    for j=1...N
        model = 將prob[i, j]中的平均跟標準差套入常態分佈
        p = p * (將X[j]的值放入model得到機率值)
    end
    prob_C[i] = p / C[i]  # 如果訓練資料都平均分佈，那其實可以不用除這項
end

以上是預測的部份
最後只要看prob_C中誰大，就預測是誰了！