聽到迴歸總是讓不是數學也不是統計背景的我退後三步，但人生就是這樣充滿了挑戰，
我們來淺淺的複習迴歸分析。

迴歸分析(Regression)一直是統計學事務所的藝人，擅長一種建立變數關係數學方程式的演算法類型，像是教育程度和收入的關係、練習量和馬拉松成績的關係等等，經過分析的方法後，我們可以實證變數關係，可以預測未來。

常見的分類有:

• 簡單線性迴歸 Simple Linear Regression 
• 羅吉斯迴歸  Logistic Regression
• 複迴歸 Multiple Regression

簡單線性迴歸是用來分析一組依變數Y和自變數X的關係:

• 如果依變數Y也是一個數值，就可以是著套線性迴歸。
• 如果依變數Y是二元型別，這時羅吉斯迴歸分析是很常使用的演算法。

自變數:Independent variable
依變數:Dependent variable

簡單迴歸表示式： 

Y = a + bX + e

a是常數
b是相關係數
e是誤差值，希望是服從常態分佈

我們在資料夾MyR新增一支Day23.R

什麼時候可以用迴歸分析?

當你覺得X和Y有關係時，就可以用!

今天會使用的是R語言的內建的cars資料集(dataset)，cars數據中有兩個欄位:
Speed 速度
dist 煞車距離

在Day23.R中輸入程式碼

#先畫散佈圖觀察

ggplot(cars, aes(x = speed, y = dist)) + geom_point(shape = 10, size = 5) 

執行結果:

訓練模型

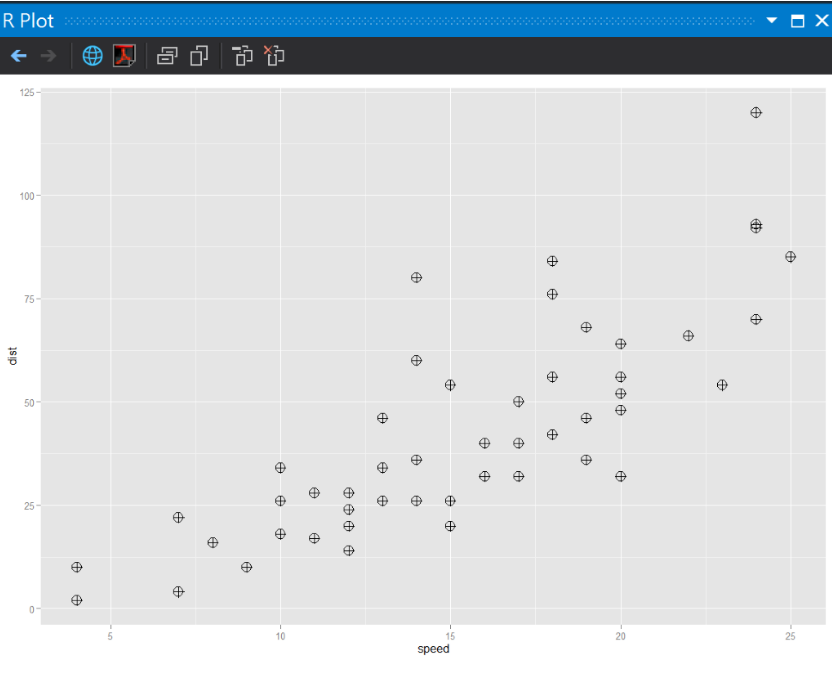
開始訓練模型，函數就是lm()，方程式(formula)的表示方式就是y~x，最後我們利用模型畫出區域 。

在Day23.R中輸入程式碼

#lm(y~x)  
carsLM <- lm(dist ~ speed, data = cars) 
#散佈圖 加上模型預測區域 
ggplot(cars, aes(x = speed, y = dist)) + geom_point(shape = 10, size = 5) + 
geom_smooth(method = lm) + labs(x = "速度", y = "煞車距離") 

執行結果:

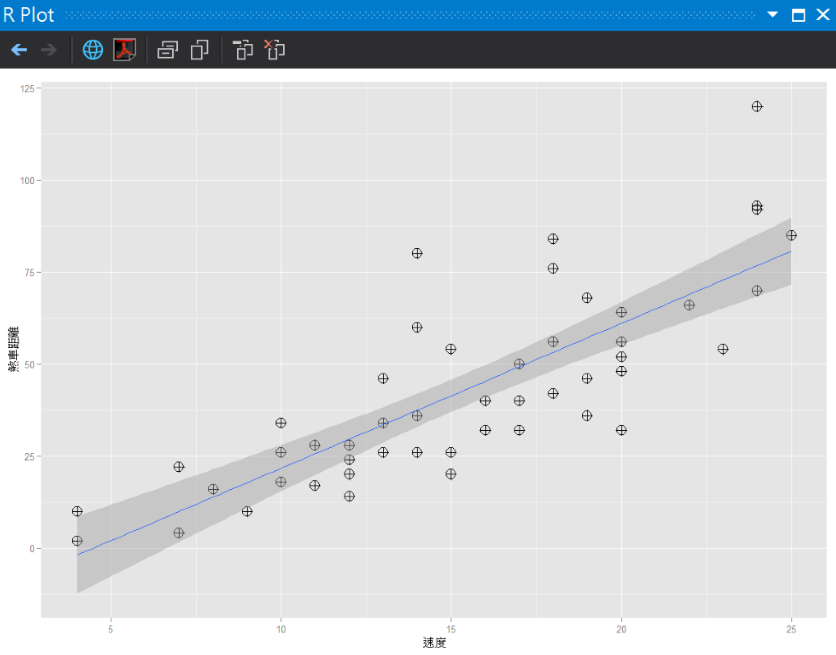
如果對散佈圖有一點點不了解，可以閱讀Day20 R語言散佈圖(Scattper Plot)。

方程式係數取得

從模型摘要summary()中取得方程式參數。

在Day23.R中輸入程式碼

summary(carsLM) 

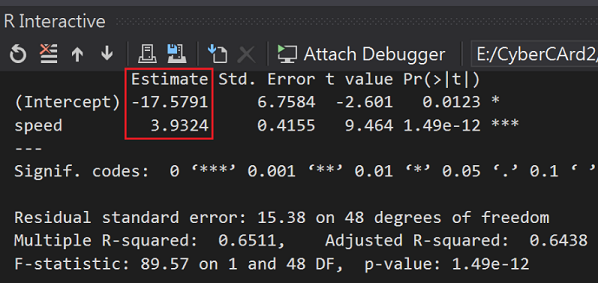
R-squared是簡單評估迴歸模型預測準度的數值，圖中為0.6438，越接近1，解釋力越強大。

另外我們回到簡單迴歸表示式：
Y = a + bX + e

可以從模型摘要中取得方程式中的參數
常數a=-17.5791
係數b=3.9324

假設速度20
Y= -17.5791 + 3.9324 * 20
=  61.0689

利用預測函數取得結果

接下來我們從predict()函數中預測結果

在Day23.R中輸入程式碼

#(4)預測 
new <- data.frame(speed = 20) 
result <- predict(carsLM, newdata = new) 
result 

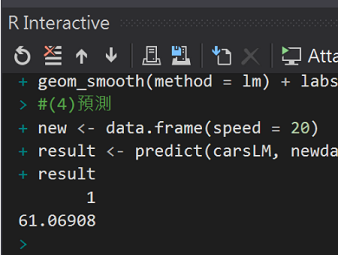
預測煞車距離61.06908

然後把預測值座標用點geom_point放在圖上，用紅色的註記顯示。

#(5)把預測座標放到圖上 
ggplot(cars, aes(x = speed, y = dist)) + geom_point(shape = 10, size = 5) + 
geom_point(x = new$speed, y = result, size = 10, shape = 17, color = "red") + 
geom_smooth(method = lm) + labs(x = "速度", y = "煞車距離") 

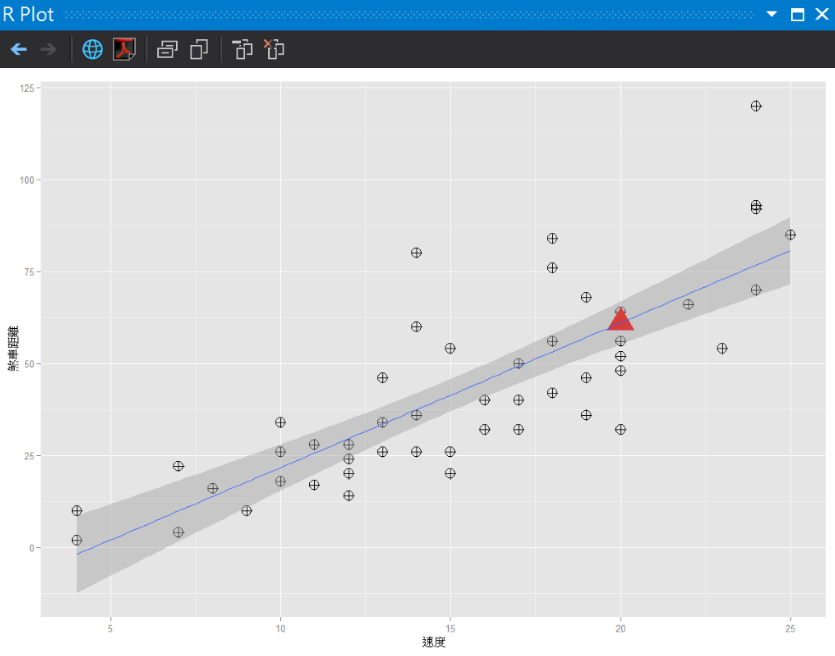
觀測用的車輛煞車應該壞了，這種速度需要這樣的煞車距離。

今天的自己又重新認識了依變數Y和自變數X的關係。

更新:

哈哈!還好有老師提點!

雖然大多數的人都知道1英哩=1.6公里左右，但是，但是，但是 1英呎= 0.3048公尺!!!

原來在英制(Imperial units)長度單位中，英哩和英呎間還有鏈(1鏈=22碼)和碼(1碼=3英呎)的單位。

好，轉換為公制(Metric Units)看一下圖:

#來個card2從英制轉換為公制
cars2 <- cars
#一英哩 = 1.6公里
cars2$speedByMetric <- cars$speed * 1.6094
#一英尺 = 0.3048公尺
cars2$distByMetric <- cars$dist * 0.3048
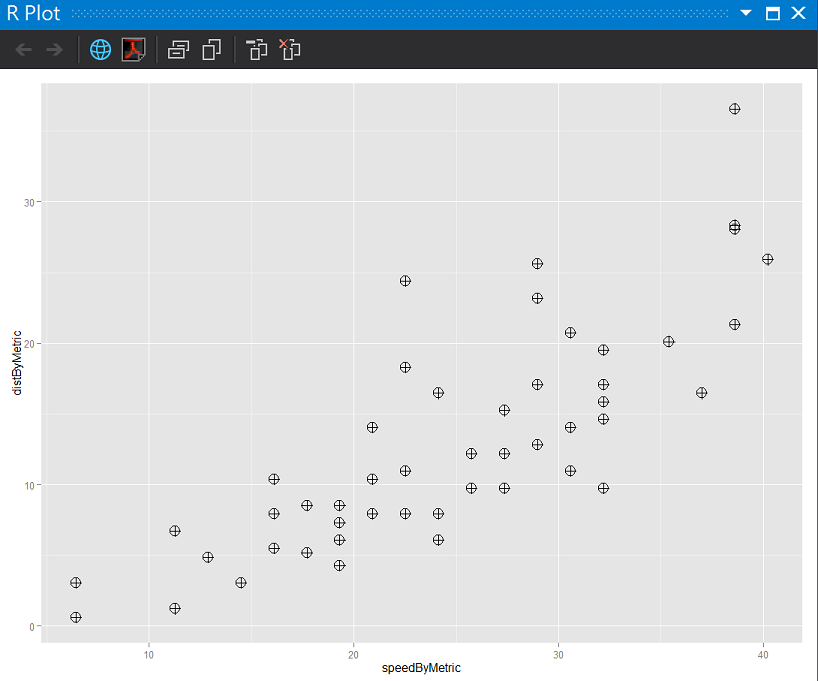
ggplot(cars2, aes(x = speedByMetric, y = distByMetric)) + geom_point(shape = 10, size = 5)

公制執行結果:

熊本城，哈!被老婆嫌不會攝影的自己也在找直線。

2015攝於熊本城，日本九州