如果你是蓋捷運的司令官，你必須要在三年內將一站捷運站蓋好。你必須要找到一位效率又高又快的工程師，越早動工越好。
很不幸的，在你發出應徵消息後的隔天，來了五十位工程師要應徵一份工作，於是你決定：為了正確評斷一個人，我一天只看一個人，只要我看到自己認為一位最好的工程師，我隔一天就叫他來指揮。
但是現在出現了一個問題：工作只能工作到一百天後，但是你卻用一百天去應徵？如果真的要這樣做的話，要怎要選才可以為工程達到最大效益呢？

先討論全部有4個人(N=4)應徵，一天的工作能力各為1,2,3,4，每天應徵一個人，應徵後如果要選他來工作的話，就必須要讓他隔天來工作，所以

如果第一個人被應徵，則會工作四天;
如果第二個人被應徵，則會工作三天;
如果第S個人被應徵，則會工作(N-S+1)天。

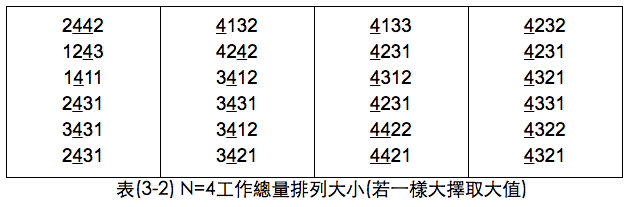
一樣將24種排法依照策略選出來並比較當S值為多少時可以為公司貢獻到最多的機率，如表(3-1)。最後再將所有最大的擺在一起，再依大小排序一次，如表(3-2)。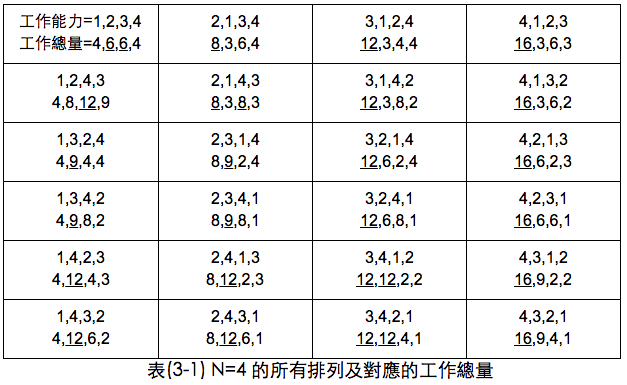

其實這個題型就跟上一個研究「凋謝速率」是一樣的事情。舉個例子：假如我在第S家，這家店的分數為X，

依照凋謝速率得到的分數為：X・(N-S+1)/N
依照工作總量得到的分數為：X・(N-S+1)

所以凋謝速率與工作總量的差別只在於有沒有除以N罷，加上凋謝速率的變因與工作總量是完全相等的，所以可以判定加上凋謝速率的問題與工作總量是等價的。

以一開始的例子來說，應徵工程師大概需要花兩個月多一點，工作時間則是兩年。所以，應徵和工作的比為 70:700=1:10 比值大約為0.1。對應到之前所說的十五條線可以找到，最好的方案可以從整個的10.6％開始拿，有29.7％的機率可以拿到最大值。

不曉得哪天想出來的問題，本來覺得又有好事可做了，但是到最後發現根本一樣啊啊啊啊啊啊啊～～～