之前的研究皆只局限於討論在「哪裡」最有可能出現「最大值」。但是，只要是出現最大值的地方平均就一定會最大嗎？於是做了下面的研究：

首先必須要知道之前的做法可以拿到的平均分數是多少，這樣我們才能知道我們所想出來的策略。

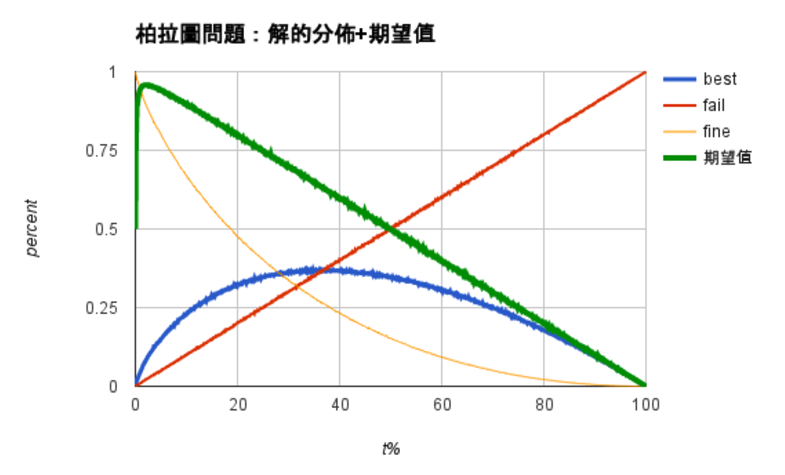
很顯然的，最大值並不是在之前提的36.8%的地方，而是在很前面2.1%的地方，我認為因為拿到最大值所佔的比例並不是很高，加上有很多連拿都沒拿到的比例會與t值成正比，所以才會在那麼前面。而且分數居然高達95.75036%，看來要繼續往上衝不是一件很簡單的事...

為了不要有到最後只能拿做後一家的情況，接下來的研究策略如下：

設有N家，
(1)第一家不要拿，
(2)從第二家開始，如果第二家不是前兩家最少的就拿取，如果不拿取的話，再到第三家;
(3)從第三家開始，如果第三家不是前三家最少的就拿取，如果不拿取的話，再到第四家;依此類推，
(4)從第N家開始，如果第N家不是前N家最少的就拿取，如果不拿取的話，再到下一家。
(5)如果到最後一家都沒有拿到任何東西的話，就只能拿取最後一家的分數。

如果我們先設N=4，總共有24種不同的排列方式，像剛剛說的策略拿一遍的話，結果會像這樣：（畫底線為拿取數字）

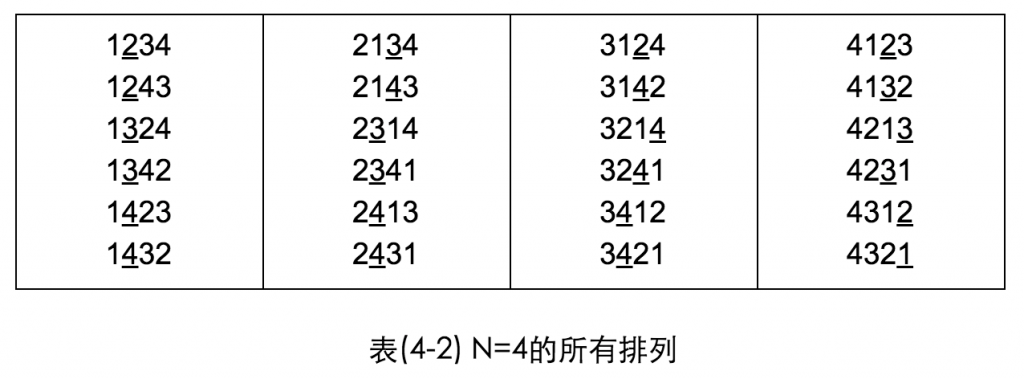
期望值為：(4x10+3x8+2x5+1x1)/24=75/24=3.125
接下來再用程式跑N=4,5,6,7,8的期望值，結果如下圖：
（隨機取球的期望值是指在其中隨便拿起一顆球的期望值）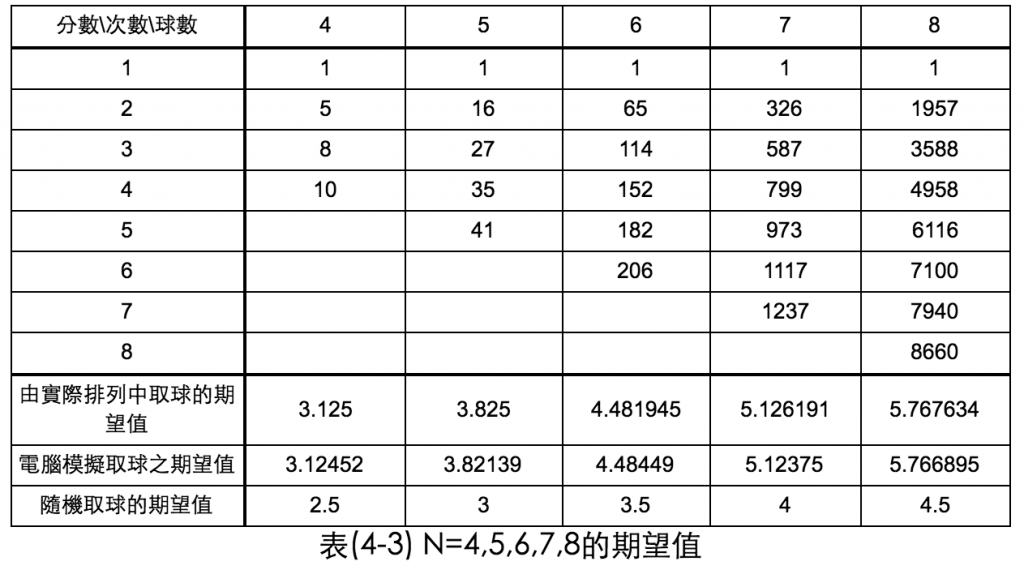


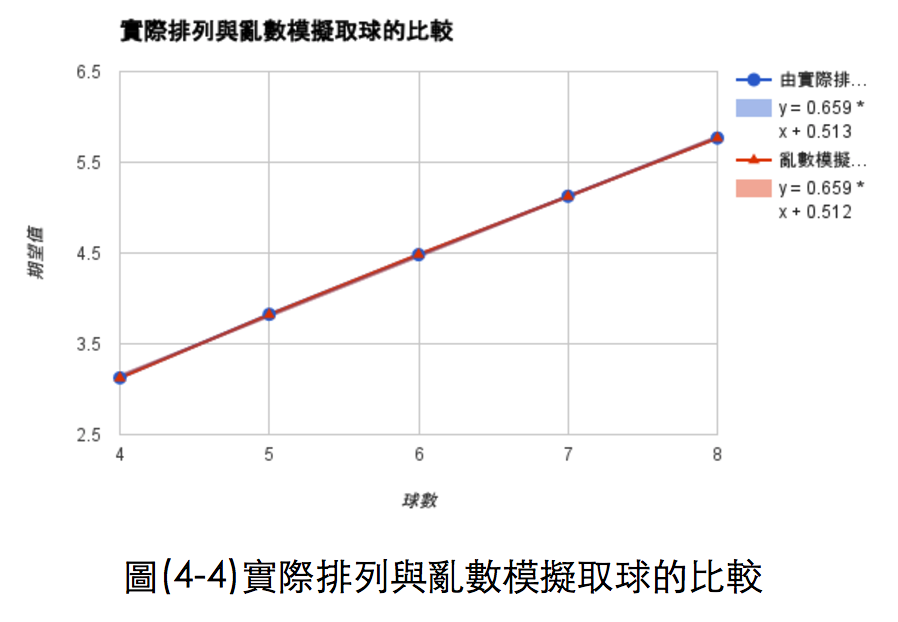
由實際排列中取球的期望值的函數為：f(x)=0.659x+0.513
由電腦模擬取球之期望值的函數為：f(x)=0.659x+0.512
兩者的函數非常接近，代表我們可以利用這個函數往更高的球數預測期望值。

函數如圖(4-5)：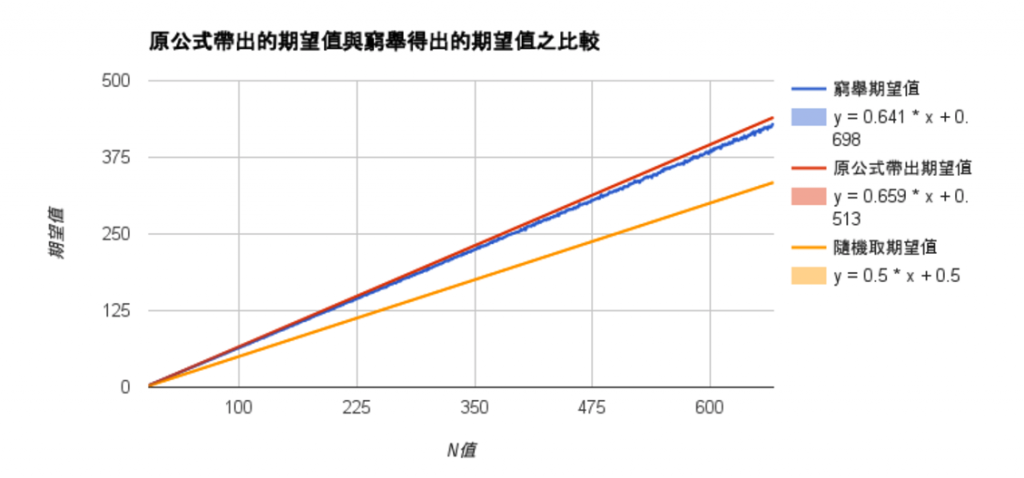

近似值得到的期望值的函數為：f(x)=0.641x+0.698，
電腦排列所得到的期望值的回歸函數為：f(x)=0.659x+0.513。
根據結果得出兩函數是相近的，推論正確。微調後得到的真正的函數為：f(x)=0.65x+0.6。

待續...