如果有真的在做資料科學的朋友對這個演算法大概也不陌生。

通常會在剛入手資料的時期用PCA看看資料的樣子，這是在探索式資料分析當中常常會用的手法，看不出個所以然的時候或許會進一步用MDS看看。

Principal component analysis

那究竟PCA是什麼？
PCA是個廣用的降維方法，當你的資料維度比較高的時候我們不容易觀察資料，我們會在資訊能夠保留的前提下，把資料的維度縮減到我們能夠觀察的維度，通常是2或3維。

PCA還可以幫助我們找出資料中的成份，這個擺到後面講。

解釋

PCA的原理其實是去找出資料中俱代表性的維度。
利用資料不同維度之間的線性組合，也就是給予不同權重計算出來的值，找出一個資料分佈上variance最大的軸。

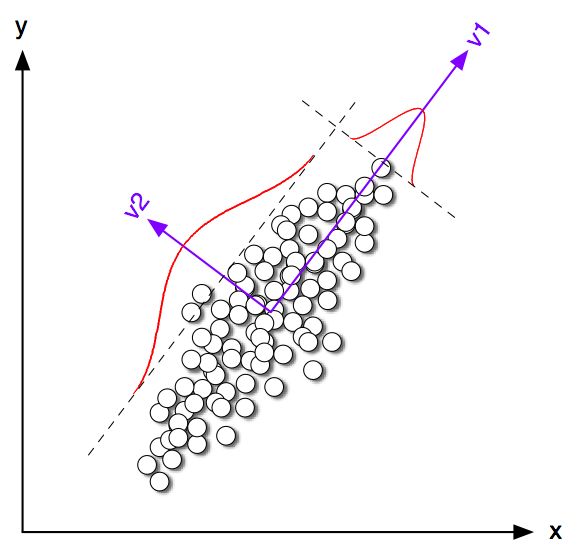
大家可以看到圖上的資料分佈，如果依照平行v1的方向展開資料的話，你可以得到資料最大的variance。

那為什麼是找最大variance的軸呢？
如果資料大家長的都差不多的話，那當中蘊含的資訊量是很少的，如果資料都長的很不一樣，當中就有很多資訊在其中，所以我們要找最大variance的方向。

找到最大的之後我們會去找出次大的，但是要求次大的軸必須跟最大的垂直，理由的話請去翻線性代數課本，接下來會依序找到跟前面的都垂直第三大的軸，當然variance愈小的話所蘊含的資訊量愈小。

原理

對於找variance這種事情，就對應到線性代數中的eigenvalue跟eigenvector！
對！沒錯！他們是同一件事！也就是你需要做的事情就是去找到前幾大的eigenvalue，他們所對應的eigenvector就是principal component，最後只要把他們選出來做一次線性轉換就可以把高維度的資料轉到低維度去了！

原理基本上就是找到一個轉換y = W^T*x，x是原始資料向量，有m維，y則是我們的目標向量，預設有n維，W是一個m-by-n的矩陣。
基本上經過轉換過後我們想要儘量的保留資訊，所以x' = W*y = W*W^T*x應該要跟原向量是一樣的，但是不保證，所以我們的loss function就會寫成sum((x - x')^2) = sum((x - W*W^T*x)^2)，一樣是用最小平方法。

應用

你可以事先決定你要降到幾維，就可以決定你要選前幾大的principal component，也就是前面講的軸，來畫圖，當然降維會帶隨資訊的流失，我們會用Pareto chart來幫助我們檢視有多少資訊流失。

圖中的長條圖代表著每個principal component所蘊含的資料量多寡，折線圖則代表累積的資訊量，所以你可以決定要在保有多少資訊量的情況下做降維，也可以看看各個principal component的資訊量分佈來決定到底要降到多少維。