今天講講我拿來做碩士論文的一個演算法。

大家或許都多多少少知道推荐系統，推荐系統需要蒐集大量的資料，像是在Amazon買書就會有哪位顧客買了哪一本書的資料。
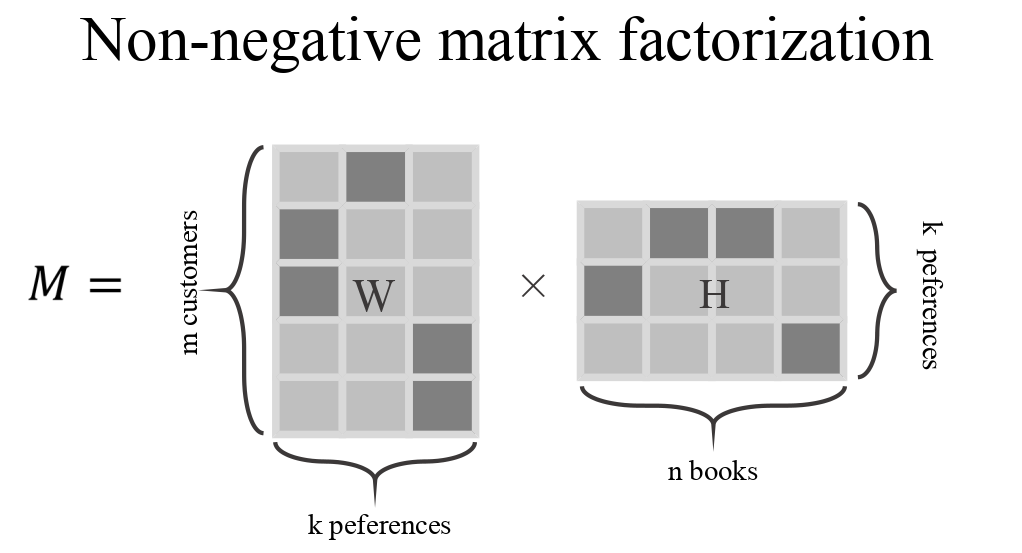
這樣的資料我們可以用一個超大型的矩陣來表示他，column是書目，row是顧客，如果有買書的話就在矩陣內記書的數量，就得到了我們的資料了！（我碩論不是做這個，這個只是比喻）

Non-negative matrix factorization

其實矩陣分解的方法有百百種，從線性代數簡單的LU分解到有名的SVD分解，絕對不缺NMF，那NMF的特色在哪裡？
重點在在於nonnegative上頭，也就是他要求矩陣當中的值必須是非負的值，當分解出來後也會是非負的值，他會產生什麼效應呢？我們後面提。

基本上這個演算法做的事情就是講一個矩陣做矩陣分解，我們會得到兩個矩陣

大家看到數學式先別害怕阿！先讓我講完，大家可以看到原本的矩陣是X，分解之後的矩陣是W跟H，那要求就是原本的矩陣跟WH相乘後的矩陣應該要愈像愈好，所以大家可以看到(X-WH)這一項，接著他被一個像絕對值的符號包起來了，這表示他是取Frobienius norm後的平方，這就跟我們的最小平方法是一致的意思！
也就是他取X跟WH的誤差是最小的情況，誤差的方法是用最小平方法！

所以到這邊大應該都看懂了。

解釋

這個模型的原理很簡單，不簡單的事他的解釋方式！
當我們要分解矩陣之前，我們要先決定分解矩陣後會多出一個維度，而這個維度的大小要設定多少？這個是大家都不知道的，需要依照不同的資料跟經驗做判斷。

分解之後出來的兩個矩陣，參考上圖，H矩陣是書目隊上一個新的維度，你可以把他想成不同的書可以被分成不同的群，所以裡面的數值就是不同的書目被歸到不同群的程度，W矩陣顧客對上一個新的維度，你可以把他想成這些客戶喜歡不同群的程度。

大家應該都有看到我將程度粗體了，這其實在解釋上有很大的空間，他其實可以是強度、偏好、歸屬程度等等解釋方式，但是總歸來說他不過就是維度做線性組合的一個權重。

所以大家可以觀察到書目可以被分成不同顧客喜好的群，而這些群又分別對應到顧客，所以這個也可以拿來作為不錯的推荐系統基礎，當有新的顧客進來的時候就可以依據他買過或是看過的書目推荐同一群當中的書目給他了！
而這樣的群我們把他稱為latent variable，也就是在這些資料裏面NMF試圖去挖掘出潛藏在資料當中隱藏的變數，而這樣隱藏的變數依據資料不同而不同，也依據分解出來的效果跟先前維度大小的決定不同，是個需要有點經驗才能上手的模型。