概述

雖然資料前處理是最為人討厭的過程，但很多時候影響結果也最深，Garbage In Garbage Out 嘛。實話說，資料的前處理沒有什麼值得讚歎的東西，就像是繁瑣的routine一樣，逐一的組合、嘗試，直到找到最好的performance。因此，以下將逐一簡介前處理的各項注意事項: 資料清理(Cleaning)、資料整合(Integration)、資料轉換(transformation)、資料切片(Discretization)。

實作資料集

這邊我拿了Kaggle上面的練習資料集Titanic來做示範，同時我會參考這一篇我自己的實作，畢竟這樣比較可以幫助大家了解並實踐。同時也很建議，大家如果有時間可以去申請一個帳號、加入這個練習比賽、下載資料集、跟著我的文章實做一遍。

資料清理的準備

由於資料清理的過程，不只是使用一次的作業，而是會不斷在未來取得資料時重複使用到的工作，所以我個人非常建議，把錢處理的過程寫成一個finction，如此只要新資料近來，只要call這個function即可。而我的習慣是透過pandas處理資料，所以我的function通常會定義如下:

#df指pandas套件中的DataFrame，用來處理表格資料很方便，可說是python中的excel
def preprocess(df): 
    ...
    ...
    return df

大家可以對照這我的實作看一下，我的preprocess的function內容大概為何。接下來寫得code全部都是出現在這個function中的段落。

資料清理(Cleaning)

處理遺漏值(Missing Value)

處理遺漏值比較常見的大概有三種方法:

1. 忽略: 這裡必須注意的是，如果你直接把具有遺漏值的資料丟掉，那麼很可能你的訓練資料量或是維度會下降。此外，你在未來預測資料時，也可能會遇到資料不全的狀況，此時總不能夠拒絕預測吧，因次建議的處理方式還是填上一些值，去測試哪一種狀況的訓練結果會比較好。
2. 補上中位數: 比竟平常的狀況會建議補上中位數，這樣相對來說不會受到極端值的影響。

df['Fare'] = df['Fare'].fillna(train['Fare'].median())
#直接把中位數填入票價的欄位中

3. 根據原本的資料分布補上亂數

# Create a New feature CategoricalAge
age_avg = df['Age'].mean()  #算出Age這個欄位的平均值
age_std = df['Age'].std()  #算出Age這個欄位的標準差
age_null_count = df['Age'].isnull().sum()  
#算出有幾個null值。df['Age'].isnull()會讓整個list為null值的部分回變成True(也就是1)，其他變為False(也就是0)。此時，算整個list的總和，就可以算出有多少個null了。
age_null_random_list = np.random.randint(age_avg - age_std, age_avg + age_std, size=age_null_count)  
# 產生出一個隨機的list，np.random.randint(最小值, 最大值, size=亂數的長度)。
df['Age'][np.isnan(dataset['Age'])] = age_null_random_list
# df後面第一個中括號索引是column index，後面的中括號則是row index，並將這些欄位填入剛產生好的亂數。

4. 根據可能的狀況補上值: 基本上這個部分要對後面要說的預測方法有點概念，不過基本上就是把遺漏值的欄位，用機器學習的方法或迴歸分析，透過其他欄位進行預測並直接填入預測值。

去除極端值(outlier)或是雜訊(noisy data)

1. 偵測: 這個部分可以透過機器學習的分群技術去尋找。也可以透過看到regression，及計算出每個資料點的residual(也就是實際值檢調預測值，也常被代稱為y-yhat)，一旦residual過大，這筆資料就很有可能有某個Feature含有極端值。另外也可以透過PCA降維(decomposition)之後直接查看，很明顯的你會發現有一些點特別跑再外面，此時可能就會存在極端值。(這段code不是出現在上面的function之內的)

X = np.matrix(df.drop(['Survived','PassengerId'], axis=1))
Y = np.array(df['Survived'])

fig = plt.figure(1, figsize=(8, 6))
ax = Axes3D(fig, elev=-150, azim=110)

X_reduced = PCA(n_components=3).fit_transform(X)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], X_reduced[:, 2], c=Y,
           cmap=plt.cm.Set1, edgecolor='k', s=40)
ax.set_title("PCA with non-log(Fare)")
ax.set_xlabel("1st eigenvector")
ax.w_xaxis.set_ticklabels([])
ax.set_ylabel("2nd eigenvector")
ax.w_yaxis.set_ticklabels([])
ax.set_zlabel("3rd eigenvector")
ax.w_zaxis.set_ticklabels([])

plt.show()

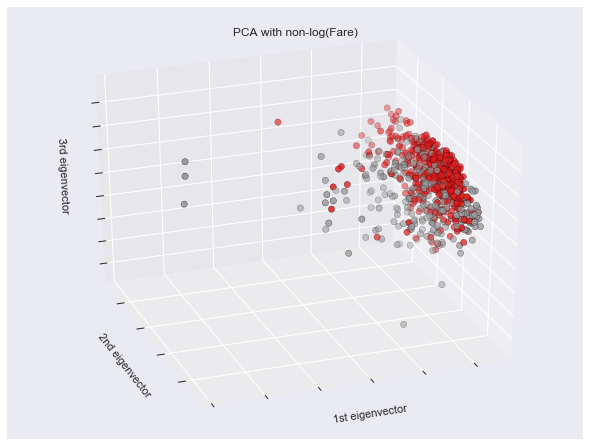
至於PCA是甚麼，因為內部運作邏輯實在太複雜，只簡單說明它的功能。PCA中文為主成分分析，其作用主要是希望方便人類視覺化觀察資料，因為實際資料可能有非常多非常多的Feature，但是一旦超過三個維度就無法視覺化呈現(除非你是下一個愛因斯坦，發現時間可以摺疊之類的。)，所以為了方便人類觀察，PCA在損失最少資訊的情況下，把所有資料投影到三個維度上面，並呈現出來。如果寫到這邊你還是霧煞煞，那我建議你，你把這個技術當作是愛因斯坦的眼睛，可以幫助你看到她眼中的資料分布，這樣你可能會好過一點。

2. 抓錯: 至於要如何判斷錯誤，大多時候還是要依些領域相關的知識的(domain knowledge)。舉例而言，假設今天你有一個大學生的資料集，其中你發現某個現在還在校的大學生，出生日期是1894年，那麼你可能就比需要處理一下這個值。不過這個例子中的知識是我們一般生活中可以判斷出來的知識，假設你今天拿到的是一個很專業的花學相關的資料集，你可能就很難了解，溫度的高低對於化學產品年濁度的影響，甚至相關的單位都沒有概念的時候，可能就比較辛苦了。

資料正規化(normalize)

另外一種狀況就是，其實不是極端值，只是剛好數字的range比較大，像這一份資料集中的Fare(車票)欄位，當直接拿來取log之後，就可以把上面那張PCA變成下面這張，實際上面perfomance也增加了一些。

def applyfun(row):
    row['Fare_log10'] = math.log(row['Fare'], 10) if  row['Fare'] != 0 else 0
    return row
df = df.apply(applyfun, axis=1)

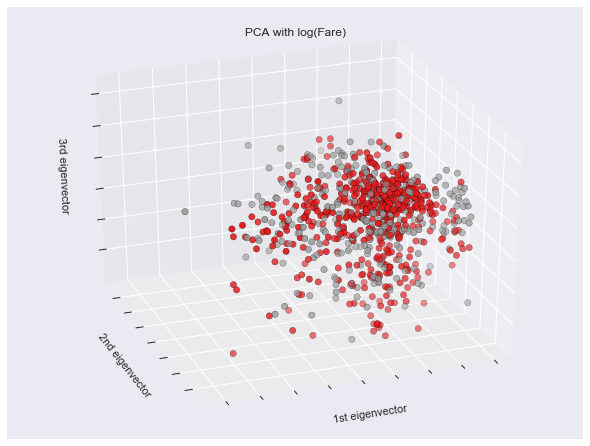
其原理其實也很好想像，我們稍微看一下取log前後的差異，大家大概就會明白了:
1. 1000000 == 10^6 => log => 6
2. 10 => 1
3. 1 => 0
4. 0 => inf(無限大)
5. 0.1 => -1
6. 10 ^ -10 => -10

所以大家會發現兩件事情。一、原本10^6跟1差了999999，但是取log之後，變成差距為6，也就把極端值變得不極端了；二、如果數字小於1，必須注意log轉換要小心負號。

資料整合(Integration)

這部分大家就比較需要資料集相關的專業知識了。舉個最簡單的例子，假設你有身高體重的資料，你希望透過這樣的資料去預測一個人會不會生病，那麼你可能可以把身高跟體重兩個欄位整理成同一欄位BMI。如果再titanic這個資料集，則可以跟各位分享一個case: 將「父母及子女」(Parch)以及「年紀」(Age)整合成「母親」(Mother)的欄位。或是「父母及子女」(Parch)以及「兄弟及配偶」(SibSp)整理成「家庭成員數」(Family_Size)。

def applyfun(row):
    row['Family_Size'] = row['SibSp'] + row['Parch']  ## 家庭成員數
    row['Is_Mother']= 1 if row['Parch'] > 1 and row['Age']>20 else 0  ## 是否為母親
    return row
df = df.apply(applyfun, axis=1)