前言

為了透過電腦強大的運算力幫助人們解決問題，首先我們的問題是需要能夠被量化與分析的。例如：給定歷年的房屋資料，預測之後的房價變化；由使用者過去的瀏覽紀錄，猜測他們可能喜歡的物品等等。

這些問題因為有明確的輸入（房屋資料、瀏覽紀錄）與輸出（房價、喜歡物品），所以可以由電腦做運算後得到答案。

機器學習的分類

機器學習主要可分為兩大類：

• 監督式學習（Supervised learning）：我們的資料有明確的輸入與預期的輸出結果，希望根據這些現有的資料來推測。例如：氣象預測就是根據過去的天氣資料來判斷當天氣條件類似時，天氣可能會如何變化。細分下去又可以再分成：
  • 迴歸：根據現有的資料來預測
  • 分類：根據現有的資料，把資料分類到正確的標籤
• 非監督式學習（Unsupervised learning）：我們的資料並沒有輸出結果，但可能有某種關係，希望透過電腦幫我們分類。例如：有許多新聞我們想要做分類，這時如果沒有資料當中沒有對新聞做標記，我們可以透過分析新聞內容的相似度，讓電腦幫我們分類。

特徵（feature）與標籤（label）

在機器學習當中，這兩個名詞會不斷的出現，現在一一來介紹：

• 特徵（feature）：資料的特徵，以房屋資料為例，土地大小就算是一種特徵；或者房屋所在地區也可以是個特徵。
• 標籤（label）：期望輸出的結果，以房屋資料為例，標籤就是房價。

所以，機器到底如何學習？

我們繼續以剛剛的房屋資料為例，如果我們現在有兩筆房屋資料：

我們可以在平面圖上把它畫出來：

如果想要用一條線表現彼此的關係呢？相信大家都看過：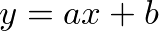

把兩點帶入就可以求得 a, b。

透過上述的方式，我們就可以知道如果房屋 20 坪的話，依照這個線性方程式的計算結果，房價會是 2000000 左右。

這就是機器學習嗎？沒錯，我們之後就會提到，事實上透過線性方程式預測資料輸出，就是線性迴歸在做的事，而它的本質就是上面看到的。

把資料轉換為數學方程式，再透過各種優化手法找到一組最佳解，就是機器學習在做的事情。

不過事情當然沒有那麼簡單，房價或許不只會受到房屋大小影響而已，在真實世界當中，我們可能會有上百個 feature 與數百萬筆的資料。所以我們需要更有效率的方法來求解。

矩陣與機器學習

矩陣幾乎是我們在高中與大學的夢魘，雖然在課堂上教授都喜歡叫我們手算矩陣，但矩陣本來就不是給人類運算用的。

為了簡化運算，在機器學習當中會大量使用到矩陣。

至於為什麼矩陣能夠簡化運算呢？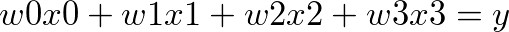

上述的操作可以用矩陣簡化為：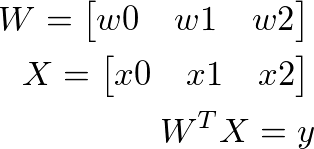

這樣一來，就不需要一直寫迴圈，許多程式庫也已經針對矩陣運算做了優化，同時矩陣也能夠直接用陣列來表示。

剛剛提到的轉置矩陣只是一個很簡單的例子，在矩陣當中有許多特性及運算（特徵向量、奇異值分解），都可以幫助我們在求解時更容易找到答案。