屬性-1

If , then
此表達式中的意思，A為B的子集合，因此A發生之機率必小於等於B發生之機率。換句話說由於A被包含於B之中，所以B可以看成由兩個區塊組成，也就是A以及是B但不是A的部分。下圖以樣本空間來表示A與B的關係: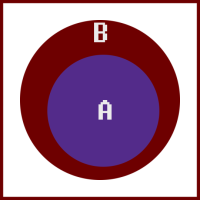

整張圖是一樣本空間，而B是此樣本空間的子集合、A是B的子集合。而上面提到的"B是由A以及是B但不是A的部分的組成"這句話則是下面這個定理:

遙想起國中時好像有這樣的片段記憶，老師在台上說著這些ABBABBABBAC的外星語言，台下的學生一點感覺都沒有，所以日子久了也就忘了這是在ABBABBABBAC什麼了。但是如果我將這張圖做一點改變，這些一開始摸不著邊際的概念就很鮮明了:

在此，樣本空間用來表示全部的人類，而B是人類中的男性，A是男性中的高富師。

可以理解為 男性(B) = 高富師的男性(A) + 不是高富師的男性(B and A^c)。
由上式則進一步推導此定理:

此定理表示當A為B的子集合時，A發生的機率必定小於等於B發生之機率，這是因為A既然是B的子集合，則A充其量等於B而不大於B。以上面的例子舉例，充其量全部的男生都是高富師，但是高富師還是男性，所以不會大於男性的範疇。

屬性-2

此定理意思為，A聯集B的發生機率等於A發生機率加上B發生機率減去A和B同時發生的機率，可用下圖做理解:

樣本空間用來表示所有男性，當我們想要計算高或富的男性在全男性中的比例時，將高的男性佔的比例加上富的男生占的比例，還需要減去重複計算的人次，也就是既高且富的男性。而順著上面的定理，我們可以在此不等式的兩端各加上
引此可以進而推導為:，也自然可以得到以下結論:

屬性-3

將定理中的A看做是高、B為富、C是師，此定理表示ABC的聯集由等式右方的三項所組成，以圖形化的方式理解:

結語

才進入正式寫文的第二天就讓我陷入一陣困頓當中，因為今天的主題是一堆數學公式，如果直接將課本上的公式複製貼上到這裡並沒有意義。花了一陣子思考後決定用比較直觀的方式來表達這些定理，但代價是花了非常多時間做圖。也許我要再三思量一下如何調整我的步伐，以更聰明的方式進行。