機率模型

在本系列文章中將探討何謂機率模型。模型泛指通過抽象和簡化表現某事物的特徵。例如某動漫人物的樹指模型是對該動漫人物特徵的簡化表現(因為樹指模型只有該動漫人物的外觀而沒有全部特徵)，而機率模型就是試圖對不確定性的現象進行刻畫。至於為什麼探討的是機率模型而不是機率本身呢?這是因為現實中不確定性的因子太過龐大，我們僅能用簡化的方式來做描述。

至於機率的嚴格定義是什麼，以是維基百科的定義:

機率論（Probability theory）是集中研究機率及隨機現象的數學分支，是研究隨機性或不確定性等現象的數學。機率論主要研究對象為隨機事件、隨機變數以及隨機過程。

機率模型的要素

匯整一機率模型有兩個步驟:

• 描述所有可能之結果
• 以機率法則來描述不同發生結果之可能性

舉例來說，當我們丟擲一銅板於地上，而因為我們並不知道結果將會如何，因此我們稱其為一隨機現象。對此隨機現象進行機率建模，第一步驟為描述擲銅板所有可能之結果或稱集合，此集合被稱為樣本空間。每個結果都稱為樣本空間內的原素，而每個元素應具備以下屬性:

• 互斥
• 集體窮舉
• 元素應擁有相同的粒度

互斥的意思是在一隨機現象結果發生後，僅有一個來自樣本空間的元素發生。集體窮舉則是所有元素構成了此樣本空間。同以擲銅板作為例子:因銅板落地後一定只有一面朝上，因此本隨機現象的所有可能也就是樣本空間為{人頭朝上,人頭朝下}。當擲銅板結果為人頭朝上時，人頭朝下的情形一定不會發生，這是符合樣本空間原素的第一項描述互斥。而此擲銅板的兩種可能結果，組成了擲銅板的所有可能結果，這是符合了第二屬性集體窮舉。

樣本空間的例子

擲銅板的例子因為情節單純，因此很容易列舉。但假設我們以一個具有四面，點數為1-4的骰子投擲兩次，該如何列舉樣本空間呢?當樣本空間不再如擲一次銅板這麼單純時，使用圖形化的方式來幫助列舉所有元素很有幫助，以下列舉兩種方式:

1.樹圖(tree diagram)

擲骰子第一次，有4種可能的結果(點數1-4)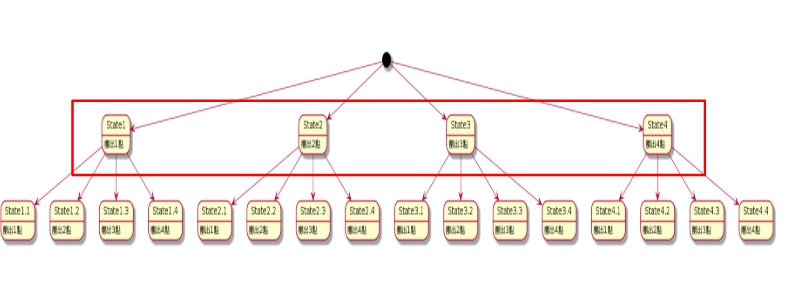

擲第二次，依照第一次擲骰子的4種可能結果，各自再發展出4種可能結果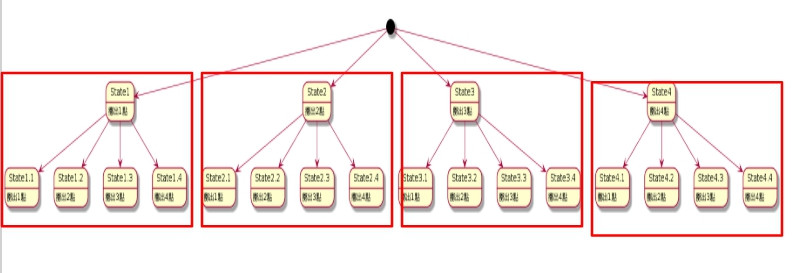

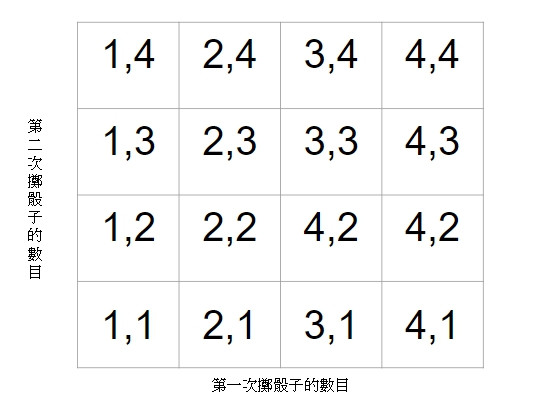
2.格狀圖

結語

此篇文章討論了機率與機率模型的基本定義，也提到彙整一機率模型時的第一步，描述樣本空間，而第二步驟將在往後的章節進行。